1. ИНФОРМАЦИЯ О РАЗРАБОТЧИКЕ ПЛАНА
2. ОБЩАЯ ИНФОРМАЦИЯ ПО УРОКУ
| Класс (укажите класс, к которому относится урок): | 7 класс |
| Место урока (по тематическому планированию ПРП) | 1 четверть |
| Тема урока | Линейное уравнение с одной переменной. |
| Уровень изучения (укажите один или оба уровня изучения (базовый, углубленный), на которые рассчитан урок): | Базовый уровень |
| Тип урока (укажите тип урока): | ☐ урок освоения новых знаний и умений ☐ урок-закрепление ☐ урок-повторение ☐ урок систематизации знаний и умений ☐ урок развивающего контроля ☐ комбинированный урок ☐ другой (впишите) |
| Планируемые результаты (по ПРП): |
| Личностные: формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи; |
| Метапредметные: Регулятивные: формулировать познавательную цель на уроке с помощью учителя и строить действия в соответствии с ней; работать по составленному плану; оценивать правильность выполнения действия; вносить коррективы и дополнения в составленные планы. Коммуникативные: уметь выражать свои мысли в устной форме; уметь слушать и слышать друг друга; выражать готовность к обсуждению разных точек зрения и выработке общей (групповой ) позиции. Познавательные: выбирать наиболее эффективные способы решения задачи; структурировать знания; применять методы информационного поиска (с помощью учебника и других средств).
|
| Предметные: понимать алгоритм решения уравнений с помощью свойств равносильности уравнений; уметь решать линейные уравнения с одной переменной; |
| Ключевые слова (введите через запятую список ключевых слов, характеризующих урок): линейное уравнение, корень уравнения, переменная, коэффициент. |
| Краткое описание (введите аннотацию к уроку, укажите используемые материалы/оборудование/электронные образовательные Данный конспект урока может быть использован для изучения темы "Решение линейных уравнений с одной переменной" по алгебре в 7 классе. Приводятся различные формы работы класса: индивидуальная, групповая, фронтальная. Использование различных видов работы на уроке повысит интерес учащихся к предмету. Учебно-методическое обеспечение: учебник алгебры, 7 класс (Макарычев Ю.Н. под ред. Теляковского С.А.)
|
3. БЛОЧНО-МОДУЛЬНОЕ ОПИСАНИЕ УРОКА
| БЛОК 1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала |
| Этап 1.1. Мотивирование на учебную деятельность |
| Укажите формы организации учебной деятельности на данном этапе урока. Опишите конкретную учебную установку, вопрос, задание, интересный факт, которые мотивируют мыслительную деятельность школьника (это интересно/знаешь ли ты, что) |
|
Историческая справка об уравнении Начиная с первого и по шестой класс вы изучали математику. А теперь, когда вы стали семиклассниками, вам выдали аж два учебника вместо одного - это «Алгебра» и «Геометрия». Сегодня у нас урок алгебры. Что же это за незнакомое слово? Мы начинаем изучать алгебру с раздела «Уравнения». И это не зря, потому что алгебра началась и долго развивалась именно как наука о уравнения. Даже само название «алгебра» произошло от слова «аль - джебр», которое известный узбекский математик IX в. Мухаммед Аль - Хорезми использовал в своей книге о решение уравнений. Первые люди уравнения умели решать очень давно. Египетские ученые почти 4 тыс. лет назад неизвестное число в уравнении называли «хау» (в переводе - «куча») и обозначали специальным знаком. В папирусе, что дошел до нас, есть такая задача: Масса и ее седьмая часть составляют 19. Найдите массу. Сегодня эта задача выглядела бы так: «Сумма неизвестного числа и его седьмой части равна 19. Найдите неизвестное число». Чтобы решить эту задачу, необходимо составить уравнение: х + 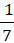 х = 19 х = 19
|
| Этап 1.2. Актуализация опорных знаний |
| Укажите формы организации учебной деятельности и учебные задания для актуализации опорных знаний, необходимых для изучения нового
|
| Давайте вспомним простые правила, Которые вы изучили еще в младших классах и по которым мы можем найти неизвестный компонент уравнения. Технология «Микрофон» Учитель задает вопросы ученикам. Ученикам предложено определенный предмет (ручка, карандаш), который будет выполнять роль микрофона. Дети передают его друг другу, по очереди беря слово. Отвечает только тот, у кого воображаемый микрофон. • Как найти неизвестное слагаемое? • Как найти неизвестное уменьшающееся? • Как найти неизвестное вычитаемое? • Как найти неизвестный множитель? • Как найти неизвестное делимое? • Как найти неизвестный делитель? • Найдите неизвестный член уравнения 5х = 50, х - 7 = 42, 18 - х = 75.
|
| Этап 1.3. Целеполагание |
| Назовите цель (стратегия успеха): ты узнаешь, ты научишься
|
| Посмотрите на тему урока, о чем мы сегодня будем говорить?: – Что называется уравнением? – Что называется корнем уравнения? – Что значит решить уравнение? – Какие уравнения называются равносильными?
|
| БЛОК 2. Освоение нового материала |
| Этап 2.1. Осуществление учебных действий по освоению нового материала |
| Укажите формы организации учебной деятельности, включая самостоятельную учебную деятельность учащихся (изучаем новое/открываем новое). Приведите учебные задания для самостоятельной работы с учебником, электронными образовательными материалам (рекомендуется обратить внимание учеников на необходимость двукратного прочтения, просмотра, прослушивания материала. 1) на общее понимание и мотивацию 2) на детали). Приведите задания по составлению плана, тезисов, резюме, аннотации, презентаций; по наблюдению за процессами, их объяснением, проведению эксперимента и интерпретации результатов, по построению гипотезы на основе анализа имеющихся данных и т.д.
|
| Вы все любите решать кроссворды. Уравнение можно тоже представить как кроссворд, где в пустую ячейку нужно поставить некоторое число. Например, 3□ - 27 = 9, но никто не рисует пустую ячейку, а на место ставит букву, называется переменной. Переменные чаще всего обозначаются буквами x и y, но можно обозначать переменную любой буквой. | Уравнение - это равенство, содержащее переменную | Если в уравнении 3х - 27 = 9 вместо переменной х написать число 12, то получим верное числовое равенство 3 ▪ 12 - 27 = 9. Говорят, что число 12 удовлетворяет данное уравнение. | Число, которое удовлетворяет уравнению, называется корнем уравнения или решением уравнения | Данное уравнение имеет только один корень - число 12. Но есть уравнения, которые могут иметь два, три и более корней или вообще не имеют корней. | Решить уравнение - значит найти все его корни или показать, что их нет | Каждое уравнение имеет левую и правую части. Так, в уравнении 3х - 27 = 9 разница 3х - 27 - это левая часть, а число 9 - права. 3х, -27, 9 - называются членами этого уравнения. Устное решение тренировочных упражнений • Какие из чисел - 2,5; 5; 7,5 - являются корнями уравнения (х - 6,5)(х + 1,5) = 9? • Составьте любое уравнение, корнем которого является число-15. • Сколько корней имеет уравнение х(х -2)(3-х) = 0? • Имеет уравнение 7 + х = х развязки? Почему? • Покажите левую и правую части уравнения 2х + 3 = 3х - 8 и назовите его члены.
|
| Этап 2.2. Проверка первичного усвоения |
| Укажите виды учебной деятельности, используйте соответствующие методические приемы. (Сформулируйте/Изложите факты/Проверьте себя/Дайте определение понятию/Установите, что (где, когда)/Сформулируйте главное (тезис, мысль, правило, закон) |
|
Создание алгоритма решения линейных уравнений. Учащиеся могут сами создать алгоритм: 1. Если выражения, стоящие в левой или правой части уравнения, содержат скобки, то раскрываем их по правилам. 2. Переносим слагаемые с переменными в левую часть уравнения, а без переменных в правую. 3. Приводим подобные слагаемые в обеих частях уравнения, приводя его к виду ax = b. 4-й шаг. Решаем получившееся линейное уравнение, равносильное исходному, в зависимости от значений коэффициентов a и b.
Найти решение уравнения: 4(x + 2) = 6 - 7x 15 – 2x = 10 + x |
| БЛОК 3. Применение изученного материала |
| Этап 3.1. Применение знаний, в том числе в новых ситуациях |
| Укажите формы организации соответствующего этапа урока. Предложите виды деятельности (решение задач, выполнение заданий, выполнение лабораторных работ, выполнение работ практикума, проведение исследовательского эксперимента, моделирование и конструирование и пр.), используйте соответствующие методические приемы (используй правило/закон/формулу/теорию/идею/принцип и т.д.; докажите истинность/ложность утверждения и т.д.; аргументируйте собственное мнение; выполните задание; решите задачу; выполните/сделайте практическую/лабораторную работу и т.д.). |
|
На необитаемом острове Робинзон Крузо научил считать своего попугая от 1 и до какого числа. Если бы это число удвоить и к результату прибавить 30, то получили бы полсотни. До какого числа научился считать попугай Робинзона Крузо? Уравнение к задаче составляется коллективно, но решают его ученики самостоятельно.
|
| Этап 3.2. Выполнение межпредметных заданий и заданий из реальной жизни |
| Подберите соответствующие учебные задания |
|
|
| Этап 3.3. Выполнение заданий в формате ГИА (ОГЭ, ЕГЭ) |
| Подберите соответствующие учебные задания |
| 1. Равносильны ли уравнения 3х+2х=15 и 5х=5? А) да; Б) нет; В) установить невозможно. 2. Является ли число 7 корнем уравнения 3х-6=х+8? А) да; Б) нет; В) установить невозможно. 3. Решить уравнение 6х+(3х-2)=16 А) 2; Б)1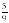 ; В) ; В) 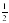 ; Г) ; Г) 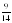 . . 4. Найдите корень уравнения – 0,3х = 6 А) 0,5; Б) -2; В) – 20; Г)- 0,05 5.Общий вид уравнения с одной переменной имеет вид: А) x=b; Б) a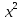 =b; В) ax=b; =b; В) ax=b; Г) ax+x=b. 6. Линейное уравнение может иметь: А) ровно два разных корня; Б) ровно три разных корня;
В) один корень; Г) ровно пять разных корней.
|
| Этап 3.4. Развитие функциональной грамотности |
| Подберите соответствующие учебные задания |
|
|
| Этап 3.5. Систематизация знаний и умений |
| Подберите учебные задания на выявление связи изученной на уроке темы с освоенным ранее материалом/другими предметами |
|
|
| БЛОК 4. Проверка приобретенных знаний, умений и навыков |
| Этап 4.1. Диагностика/самодиагностика |
| Укажите формы организации и поддержки самостоятельной учебной деятельности ученика, критерии оценивания |
| Учитель формулирует незаконченное предложение и предлагает учащимся высказаться относительно итога урока, заканчивая его. Каждый следующий участник обсуждения должен начинать свое выступление с предложенной формулы. Учащиеся работают с открытыми предложениями: «На сегодняшнем шаге мы узнали...», «На сегодняшнем шаге важнейшим открытием для меня было...» и «В начале урока я поставил перед собой цель. Вот как я ее достиг...»
|
| БЛОК 5. Подведение итогов, домашнее задание |
| Этап 5.1. Рефлексия |
| Введите рекомендации для учителя по организации в классе рефлексии по достигнутым либо недостигнутым образовательным результатам |
|
Продолжите ФРАЗЫ… Сегодня я узнал… Было интересно… Было трудно… Я выполнял задания… Я понял, что… Теперь я могу… Я почувствовал, что… Я приобрёл… Я научился… У меня получилось… Я смог… Я попробую… Меня удивило… Урок дал мне для жизни… Мне захотелось… Расскажу дома, что …
|
| Этап 5.2. Домашнее задание |
| Введите рекомендации по домашнему заданию. |
| Учитель предлагает каждому обучающемуся: 1. Карточку для работы с текстом параграфа по плану: | Выделите в тексте главные смысловые части Найдите по тексту ответы на вопросы: что такое: а) линейное уравнение, б) корень уравнения, в) решить уравнение? Какие бывают случаи решения линейного уравнения? Сколько решений может иметь: а) линейное уравнение, б) нелинейное уравнение? Найдите в тексте слова-ориентиры; Найдите в тексте учебника разъяснение того, как решается: а) линейное уравнение; б) задача с помощью линейного уравнения; Найдите в Интернет-ресурсах понятие «уравнение». Найдите исторические факты «как люди научились решать уравнения». Найдите в литературе, Интернет-ресурсах примеры старинных задач, решаемых с помощью уравнений. | №128 (ж,з,и), №130(2 столбик)
|
















