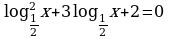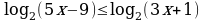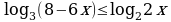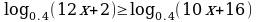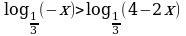Просмотр содержимого документа
«Практическая работа: «Решение логарифмических уравнений и неравенств»»
Практическая работа №5
Тема: «Решение логарифмических уравнений и неравенств»
Цель: закрепить навыки решения логарифмических уравнений и неравенств.
Теоретическая часть.
Логарифмическими уравнениями называются уравнения, содержащие переменную под знаком логарифма (в частности, в основании логарифма).
Теорема
Если 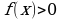 и
и 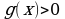 , то логарифмическое уравнение
, то логарифмическое уравнение 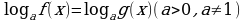 равносильно уравнению
равносильно уравнению 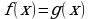 .
.
Переход от уравнения 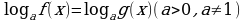 к уравнению
к уравнению 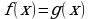 называется потенцированием.
называется потенцированием.
Основные методы решения логарифмических уравнений.
Функционально-графический метод.
Метод потенцирования.
Метод введения новой переменной.
Метод логарифмирования.
Логарифмическими неравенствами называются неравенства вида
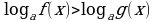 , где
, где 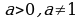 , и неравенства, сводящиеся к этому виду.
, и неравенства, сводящиеся к этому виду.
Теорема.
Если 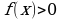 и
и 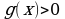 , то:
, то:
при 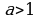 логарифмическое неравенство
логарифмическое неравенство 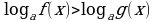 равносильно неравенству того же смысла:
равносильно неравенству того же смысла: 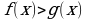 ;
;
при  логарифмическое неравенство
логарифмическое неравенство 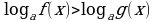 равносильно неравенству противоположного смысла:
равносильно неравенству противоположного смысла: 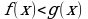 .
.
На практике теорему применяют следующим образом:
при 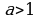 от неравенства
от неравенства 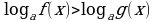 переходят к равносильной ему системе неравенств
переходят к равносильной ему системе неравенств 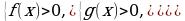
а при  :
: 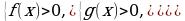
Практическая часть.
Задание №1. Решите уравнение:
а)  б)
б) 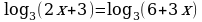
а)  б)
б)
а) 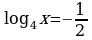 б)
б)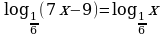
а)  б)
б)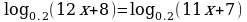
Задание №2. Решите уравнение:
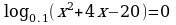
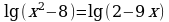
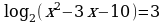
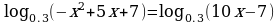
Задание №3. Решите уравнение:
а) 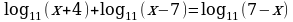 б)
б) 
а) 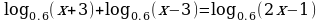 б)
б) 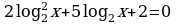
а) 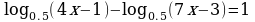 б)
б) 
а) 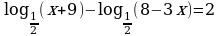 б)
б) 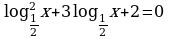
Задание №4. Решите неравенство:
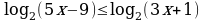
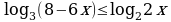
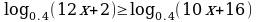
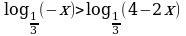
Задание №5. Решите неравенство:
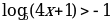
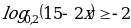 .
.
 .
.
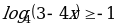 .
.
Сделайте вывод о проделанной работе
Контрольные вопросы:
Какие уравнения называются логарифмическими?
При каких условиях уравнение 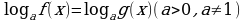 равносильно уравнению
равносильно уравнению 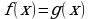 ?
?
Перечислите основные методы решения логарифмических уравнений.







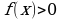 и
и 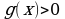 , то логарифмическое уравнение
, то логарифмическое уравнение 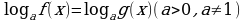 равносильно уравнению
равносильно уравнению 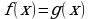 .
.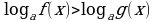 , где
, где 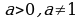 , и неравенства, сводящиеся к этому виду.
, и неравенства, сводящиеся к этому виду.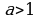 логарифмическое неравенство
логарифмическое неравенство 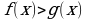 ;
; логарифмическое неравенство
логарифмическое неравенство 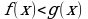 .
.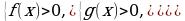
 б)
б) 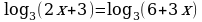
 б)
б)
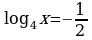 б)
б)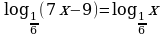
 б)
б)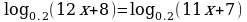
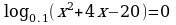
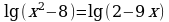
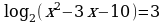
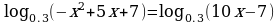
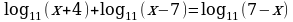 б)
б) 
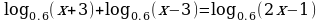 б)
б) 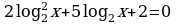
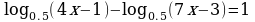 б)
б) 
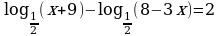 б)
б)