ПРАКТИЧЕСКАЯ РАБОТА №11
«Вычисление производных сложных функций»
ЦЕЛЬ РАБОТЫ:
Корректировать знания, умения и навыки в теме: «Вычисление производных сложных функций».
Закрепить и систематизировать знания по теме.
Определить уровень усвоения знаний, оценить результат деятельности студента.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблица производных элементарных функций.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
Ответить на контрольные вопросы:
а) Какая функция называется сложной? Приведите примеры сложных функций.
б) Сформулируйте правило вычисления производной сложной функции.
По образцу выполнить тренировочные задания.
Изучить условие заданий для практической работы.
Оформить отчет о работе.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ
ПРИМЕР 1. Заданы функции 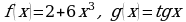 . Задайте формулой сложную функцию h, если: а)
. Задайте формулой сложную функцию h, если: а) 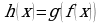 ; б)
; б) 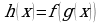 .
.
РЕШЕНИЕ. а) Функцию h можно представить в виде сложной функции 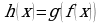 таким образом:
таким образом:
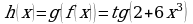 .
.
б) Функцию h можно представить в виде сложной функции 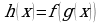 таким образом:
таким образом:
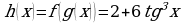 .
.
ПРИМЕР 2. Задайте формулами элементарные функции f и g, из которых составлена сложная функция 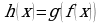 : а)
: а) 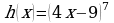 ; б)
; б) 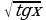 .
.
РЕШЕНИЕ. а) Функцию h можно представить в виде сложной функции 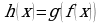 , где
, где
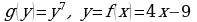 .
.
б) Функцию h можно представить в виде сложной функции 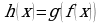 , где
, где 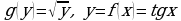 .
.
ПРИМЕР 3. Найдите производные сложных функций: а) 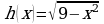 ; б)
; б) 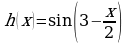 .
.
РЕШЕНИЕ. а) Так как 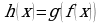 , где
, где 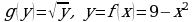 , то
, то 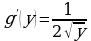 и
и 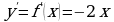 , откуда
, откуда 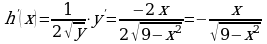 .
.
б) Так как 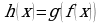 , где
, где 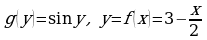 , то
, то 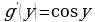 и
и 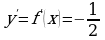 , откуда
, откуда 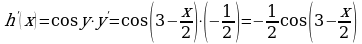 .
.
ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ.
Задайте формулами элементарные функции f и g, из которых составлена сложная функция 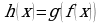 , если
, если 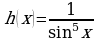 .
.
Найдите производную сложной функции 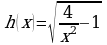 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ Задания
Задание 1. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 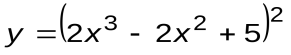
| Вариант 9 | 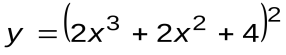
|
| Вариант 2 | 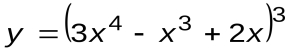
| Вариант 10 | 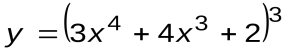
|
| Вариант 3 | 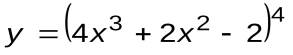
| Вариант 11 | 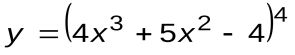
|
| Вариант 4 | 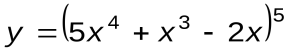
| Вариант 12 | 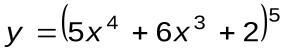
|
| Вариант 5 | 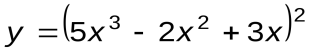
| Вариант 13 | 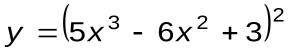
|
| Вариант 6 | 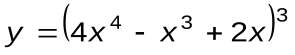
| Вариант 14 | 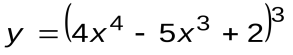
|
| Вариант 7 | 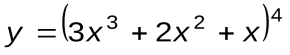
| Вариант 15 | 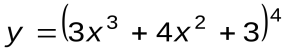
|
| Вариант 8 | 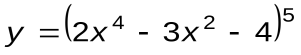
| Вариант 16 | 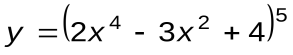
|
Задание 2. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 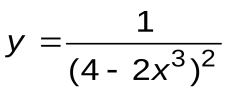
| Вариант 9 | 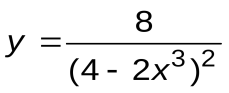
|
| Вариант 2 | 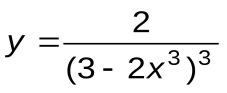
| Вариант 10 | 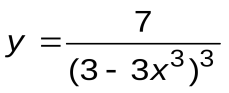
|
| Вариант 3 | 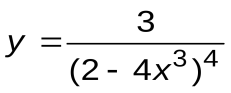
| Вариант 11 | 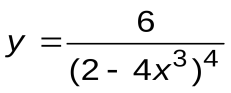
|
| Вариант 4 | 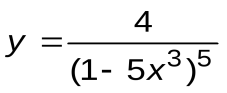
| Вариант 12 | 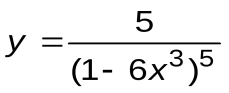
|
| Вариант 5 | 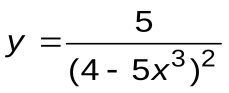
| Вариант 13 | 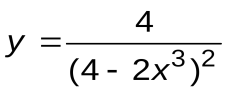
|
| Вариант 6 | 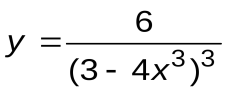
| Вариант 14 | 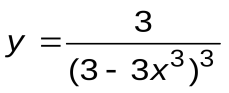
|
| Вариант 7 | 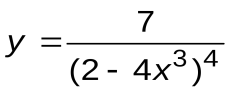
| Вариант 15 | 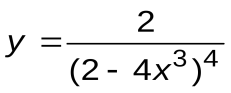
|
| Вариант 8 | 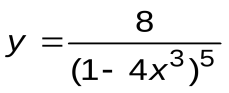
| Вариант 16 | 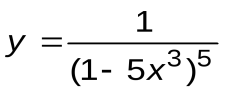
|
Задание 3. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 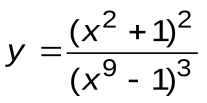
| Вариант 9 | 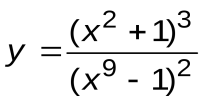
|
| Вариант 2 | 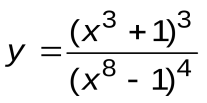
| Вариант 10 | 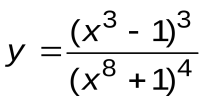
|
| Вариант 3 | 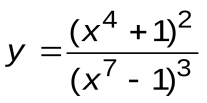
| Вариант 11 | 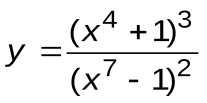
|
| Вариант 4 | 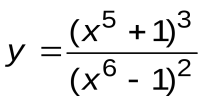
| Вариант 12 | 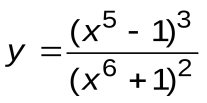
|
| Вариант 5 | 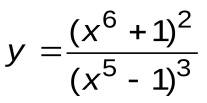
| Вариант 13 | 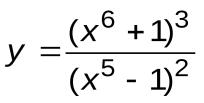
|
| Вариант 6 | 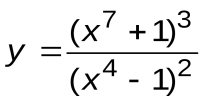
| Вариант 14 | 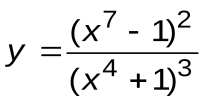
|
| Вариант 7 | 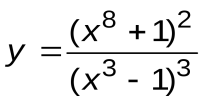
| Вариант 15 | 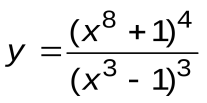
|
| Вариант 8 | 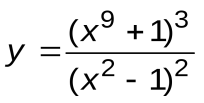
| Вариант 16 | 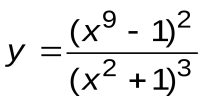
|
Задание 4. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 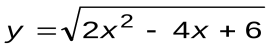
| Вариант 9 | 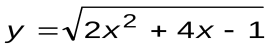
|
| Вариант 2 | 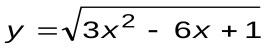
| Вариант 10 | 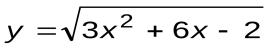
|
| Вариант 3 | 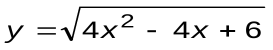
| Вариант 11 | 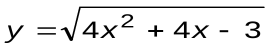
|
| Вариант 4 | 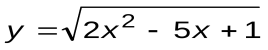
| Вариант 12 | 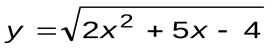
|
| Вариант 5 | 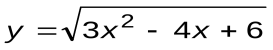
| Вариант 13 | 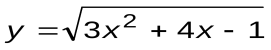
|
| Вариант 6 | 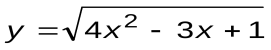
| Вариант 14 | 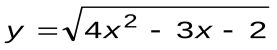
|
| Вариант 7 | 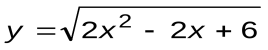
| Вариант 15 | 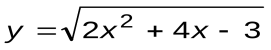
|
| Вариант 8 | 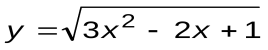
| Вариант 16 | 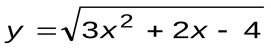
|
Задание 5. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 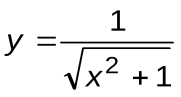
| Вариант 9 | 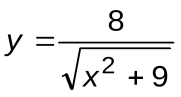
|
| Вариант 2 | 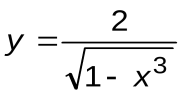
| Вариант 10 | 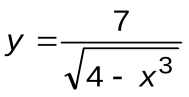
|
| Вариант 3 | 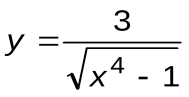
| Вариант 11 | 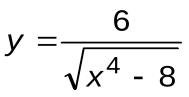
|
| Вариант 4 | 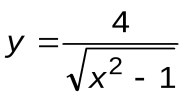
| Вариант 12 | 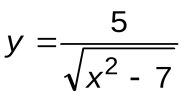
|
| Вариант 5 | 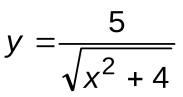
| Вариант 13 | 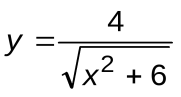
|
| Вариант 6 | 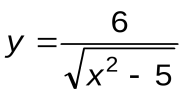
| Вариант 14 | 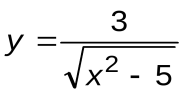
|
| Вариант 7 | 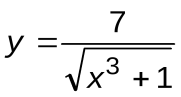
| Вариант 15 | 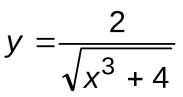
|
| Вариант 8 | 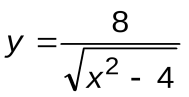
| Вариант 16 | 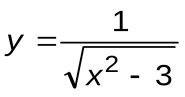
|
Задание 6. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 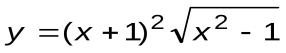
| Вариант 9 | 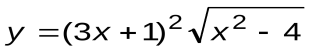
|
| Вариант 2 | 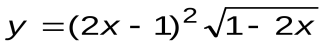
| Вариант 10 | 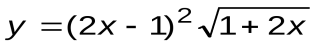
|
| Вариант 3 | 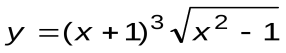
| Вариант 11 | 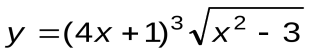
|
| Вариант 4 | 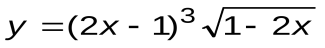
| Вариант 12 | 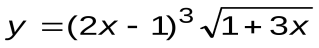
|
| Вариант 5 | 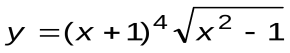
| Вариант 13 | 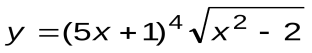
|
| Вариант 6 | 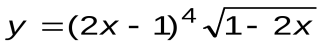
| Вариант 14 | 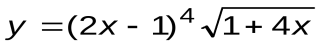
|
| Вариант 7 | 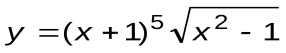
| Вариант 15 | 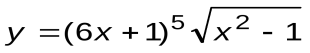
|
| Вариант 8 | 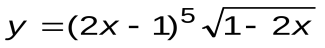
| Вариант 16 | 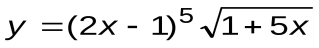
|
Задание 7. Вычислить производные следующих функций:
| № варианта | Исходные данные | № варианта | Исходные данные |
| Вариант 1 | 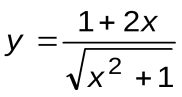
| Вариант 9 | 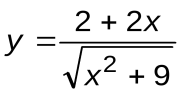
|
| Вариант 2 | 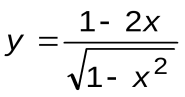
| Вариант 10 | 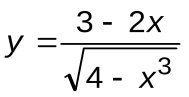
|
| Вариант 3 | 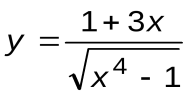
| Вариант 11 | 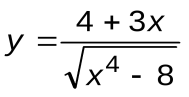
|
| Вариант 4 | 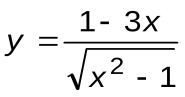
| Вариант 12 | 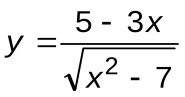
|
| Вариант 5 | 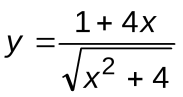
| Вариант 13 | 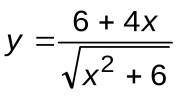
|
| Вариант 6 | 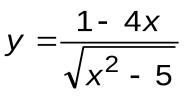
| Вариант 14 | 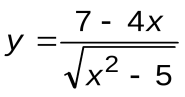
|
| Вариант 7 | 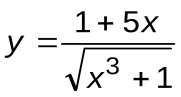
| Вариант 15 | 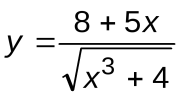
|
| Вариант 8 | 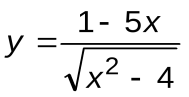
| Вариант 16 | 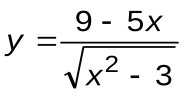
|
Задания на «4» и «5»
Вариант 1,9
Вычислите производные сложных функций:
а) 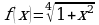 ; б)
; б) 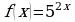 ; в)
; в) 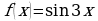 ;
;
г) 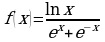 ; д)
; д) 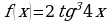 .
.
Вариант 2,10
Вычислите производные сложных функций:
а) 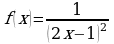 ; б)
; б) 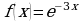 ; в)
; в) 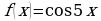 ;
;
г) 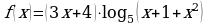 ; д)
; д) 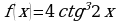 .
.
Вариант 3,11
Вычислите производные сложных функций:
а) 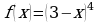 ; б)
; б) 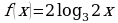 ; в)
; в) 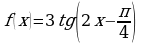 ;
;
г) 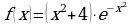 ; д)
; д) 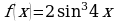 .
.
Вариант 4,12
Вычислите производные сложных функций:
а) 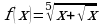 ; б)
; б) 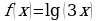 ; в)
; в) 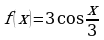 ;
;
г) 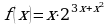 ; д)
; д) 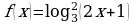 .
.
Вариант 5,13
Вычислите производные сложных функций:
а) 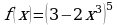 ; б)
; б) 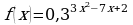 ; в)
; в) 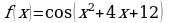 ;
;
г) 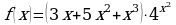 ; д)
; д) 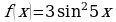 .
.
Вариант 6,14
Вычислите производные сложных функций:
а) 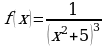 ; б)
; б) 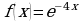 ; в)
; в) 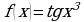 ;
;
г) 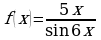 ; д)
; д) 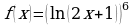 .
.
Вариант 7,15
Вычислите производные сложных функций:
а) 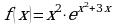 ; б)
; б) 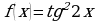 ; в)
; в) 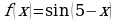 ;
;
г) 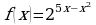 ; д)
; д) 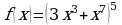 ;
;
Вариант 8,16
а) 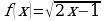 ; б)
; б) 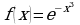 ; в)
; в) 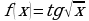 ;
;
г) 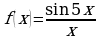 ; д)
; д) 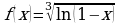 .
.





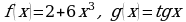 . Задайте формулой сложную функцию h, если: а)
. Задайте формулой сложную функцию h, если: а) 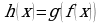 ; б)
; б) 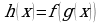 .
.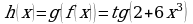 .
.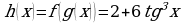 .
.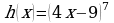 ; б)
; б) 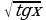 .
.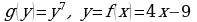 .
.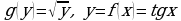 .
.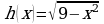 ; б)
; б) 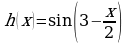 .
.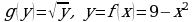 , то
, то 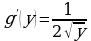 и
и 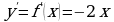 , откуда
, откуда 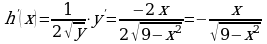 .
.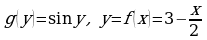 , то
, то 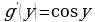 и
и 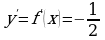 , откуда
, откуда 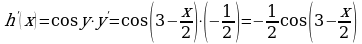 .
.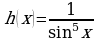 .
.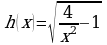 .
.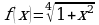 ; б)
; б) 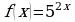 ; в)
; в) 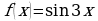 ;
; 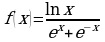 ; д)
; д) 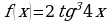 .
. 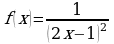 ; б)
; б) 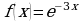 ; в)
; в) 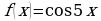 ;
; 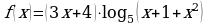 ; д)
; д) 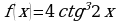 .
.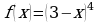 ; б)
; б) 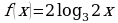 ; в)
; в) 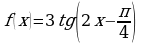 ;
; 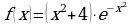 ; д)
; д) 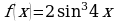 .
.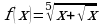 ; б)
; б) 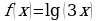 ; в)
; в) 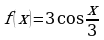 ;
; 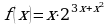 ; д)
; д) 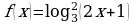 .
.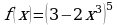 ; б)
; б) 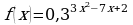 ; в)
; в) 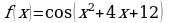 ;
; 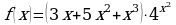 ; д)
; д) 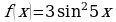 .
.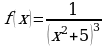 ; б)
; б) 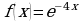 ; в)
; в) 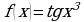 ;
; 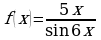 ; д)
; д) 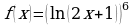 .
.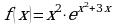 ; б)
; б) 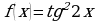 ; в)
; в) 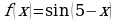 ;
; 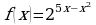 ; д)
; д) 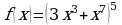 ;
;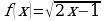 ; б)
; б) 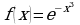 ; в)
; в) 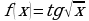 ;
; 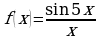 ; д)
; д) 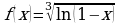 .
.









