Практическое применение теоремы Пифагора

Оркина Е.В.

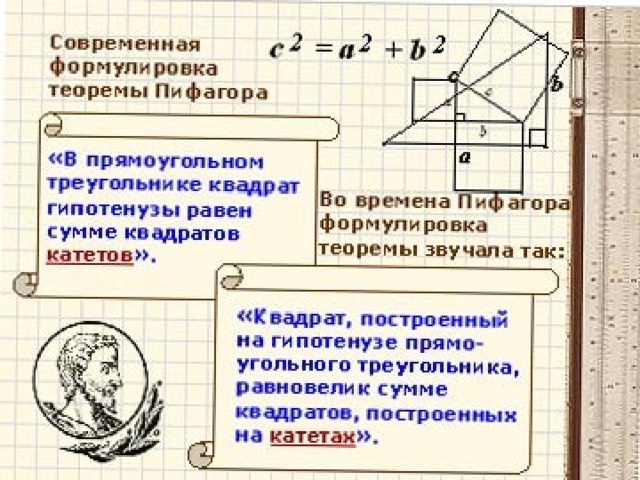
17

12

13

ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК

3:4:5

Задача Бхаскари

«На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота? »

Решение: По теореме Пифагора АВ 2 = ВС 2 +АС 2 ;9+16=25, АВ=5 Футов; СD=3+5=8 футов. Ответ: высота тополя 8 футов

Задача из китайской « Математики в девяти книгах »

«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды, и какова длина камыша?».

Решение: По теореме Пифагора (x+1) 2 =x 2 +25; 2x=24, x=12 чи.; 12+1=13 чи. Ответ: глубина воды-12 чи, длина камыша-13 чи.

Задача из учебника « Арифметика » Леонтия Магницкого

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

Решение: ВС 2 =АВ 2 -АС 2 ; ВС 2 =15625-13689=44 стоп. Ответ: ВС=44 стоп.

Задача о бамбуке из древнекитайского трактата "Гоу-гу"

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).Какова высота бамбука после сгибания?

Решение: (10-x) 2 =x 2 -9; -20x=9-100, -20x=-109, x=109/20 чи. Ответ: x= 4,55 чи.

ОБЛАСТИ ПРИМЕНЕНИЯ ТЕОРЕМЫ ПИФАГОРА :

• Архитектура
• Астрономия
• Мобильная связь

Очень легко можно воспроизвести способ построения "натягивателями веревок" прямых углов при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Окна в готической и

романской архитектуре

Строительство крыш

Молниеотвод

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты .

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе

• Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
• Решение:
•        Пусть AB= x , BC=R=200 км , OC= r =6380 км.
• OB=OA+AB OB=r + x.
• Используя теорему Пифагора,
• получим
• Ответ: 2,3 км.

Мобильная связь

• В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно , было решено п ередать обитателям Марса сигнал в виде теоремы Пифагора . Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Применение

теоремы Пифагора

в математике

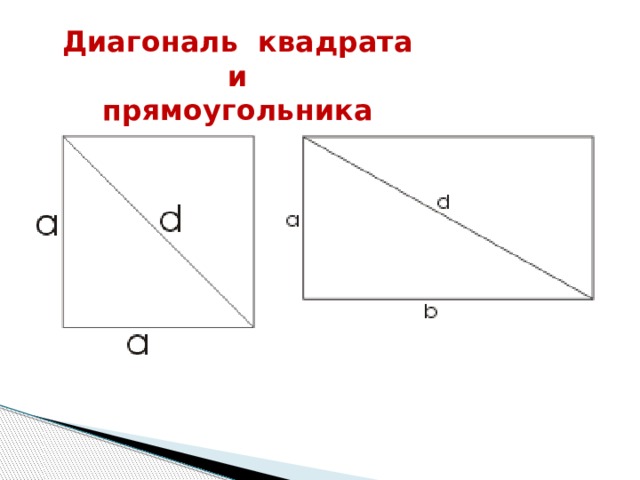
Диагональ квадрата и

прямоугольника

Высота правильного треугольника

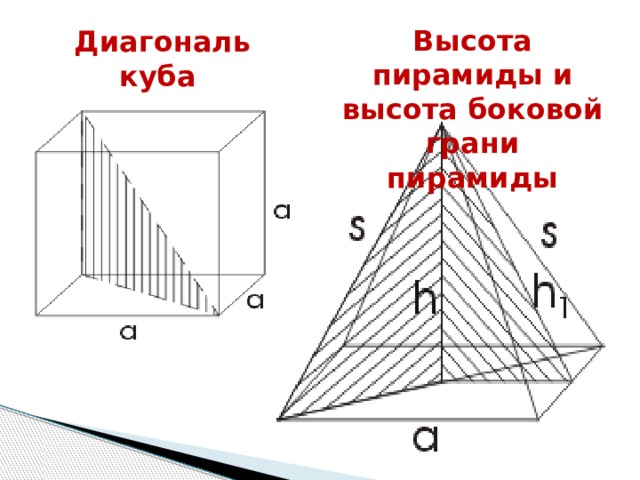
Высота пирамиды и высота боковой грани пирамиды

Диагональ куба

Длина отрезка

на координатной

плоскости

Модуль

вектора

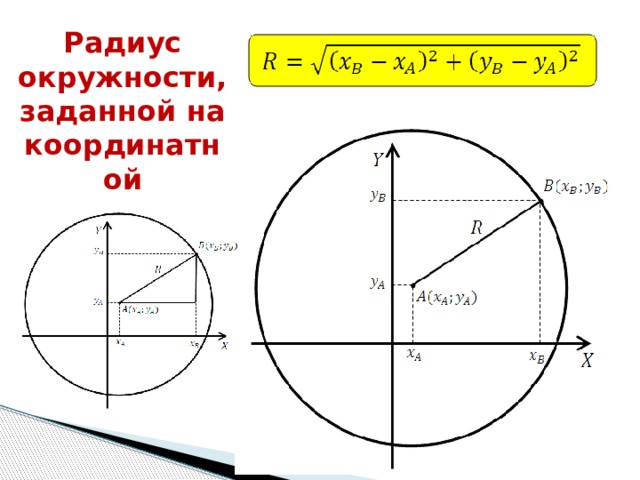
Радиус окружности, заданной на координатной плоскости

Решение задач

Ответ: 8 и 15 .

Решение задач

Ответ:

Решение задач

Ответ: 6 и 8 .

Решение задач

Ответ: 5 .

Решение задач

Ответ:

Решение задач

Ответ:

Спасибо за урок!

Д/З:

№ 10.071-10.073