Практическое занятие по теме "Многогранники"

Кейс: Геометрические построения с использованием многогранников

Задание 1: Построение правильной пирамиды

Задача: Постройте правильную четырехугольную пирамиду с основанием ABCD и вершиной S, где высота пирамиды равна h. Найдите сечение этой пирамиды плоскостью, проходящей через вершины A, B и середину ребра SC.

Решение:

1. Нарисуйте основание пирамиды — квадрат ABCD.

2. Отметьте точку S над центром квадрата (например, на высоте h).

3. Через точки A, B и середину отрезка SC проведите секущую плоскость.

4. Определите линии пересечения этой плоскости с гранями пирамиды.

5. Изобразите полученное сечение.

Подсказки:

- Используйте свойства симметрии и равнобедренность треугольника для упрощения расчетов.

- Сечение будет представлять собой трапецию.

Задание 2: Сечения куба

Задача: В кубе ABCDEFGH с длиной ребра a найдите площадь сечения, образованного плоскостью, проходящей через середины ребер AD, CF и EH.

Решение:

1. Начертите куб.

2. Обозначьте середины указанных ребер (M, N, K соответственно).

3. Проведите секущую плоскость через эти три точки.

4. Опишите форму полученного сечения (это будет правильный шестиугольник).

5. Рассчитайте площадь шестиугольника, используя формулу площади правильного многоугольника.

Подсказки:

- Площадь правильного шестиугольника со стороной s вычисляется по формуле .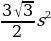

- Сторона шестиугольника будет равна половине диагонали грани куба.

Задание 3: Сечение призмы

Задача: В правильной шестиугольной призме ABCDEF. A₁B₁C₁D₁E₁F₁ с высотой h и стороной основания a постройте сечение плоскостью, проходящей через точки A, C₁ и середину ребра D₁E₁. Найдите площадь этого сечения.

Решение:

1. Нарисуйте призму.

2. Обозначьте указанные точки.

3. Проведите секущую плоскость.

4. Описать форму сечения (это будет неправильный пятиугольник).

5. Разделите пятиугольник на простые фигуры (треугольники и трапеция) и вычислите их площади.

6. Сложите полученные значения площадей.

Подсказки:

- Используйте метод деления сложной фигуры на более простые части.

- Для нахождения высоты треугольников и трапеций применяйте теорему Пифагора.

Задание 4: Пересечение двух тетраэдров

Задача: Два правильных тетраэдра ABCD и A'B'C'D' расположены таким образом, что их центры совпадают, а ребра параллельны друг другу. Найдите объем общей части этих двух тел.

Решение:

1. Представьте два тетраэдра с одинаковыми размерами, но повернутых относительно друг друга.

2. Определите общие элементы обоих тел (они будут пересекаться по некоторому октаэдру).

3. Вычислите объем октаэдра, который является пересечением двух тетраэдров.

Подсказки:

- Объем октаэдра можно найти, зная длину его ребра.

- Длина ребра октаэдра связана с длиной ребра исходного тетраэдра.

Задание 5: Секущая плоскость через грани икосаэдра

Задача: В правильном икосаэдре с длиной ребра a постройте сечение плоскостью, проходящей через середины трех соседних граней. Какова форма этого сечения?

Решение:

1. Изобразите икосаэдр.

2. Найдите середины трех соседних граней.

3. Проведите через эти точки плоскость.

4. Опишите форму полученного сечения (это будет правильный пятиугольник).

Подсказки:

- Использовать симметрию икосаэдра для упрощения задачи; Правильный пятиугольник имеет углы 108⁰.