Данная практическая работа предназначена для студентов 1 курса после прохождения темы "Комплексные числа". Данная работа состоит из двух частей: теоретической и практической. Даны указания по проведению работы, сормулированы основные цели, задачи, дано описание хода работы.
Просмотр содержимого документа
«Практическая работа по теме "Действия с комплексными числами"»
Практическая работа
по теме «Комплексные числа»
Действия с комплексными числами.
Практическая работа № 4.
Цели: формировать умение графического изображения комплексных чисел, выполнения арифметических операций с комплексными числами.
Оборудование: тетрадь для практических работ, ручка, простой карандаш, линейка, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения и контрольных вопросов. Не забывайте о правильном оформлении решения. Каждое правильно выполненное задание оценивается определенным количеством баллов.
Порядок выполнения работы
Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
Решите самостоятельную работу. Оформите решение письменно в тетради.
Ответьте письменно на контрольные вопросы.
Ход работы
Теоретический материал.
Изображение комплексных чисел.
Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi.
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Сопряжённые комплексные числа имеют одинаковый модуль
Рассмотрим на плоскости декартову прямоугольную систему координат xOy . Каждому комплексному числу z = a + bi можно сопоставить точку с координатами (a;b) , и наоборот, каждой точке с координатами (c;d) можно сопоставить комплексное число w = c + di . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.
Пример. Изобразим на комплексной плоскости числа
Z1 = 2 + i; z2 = 3i; z3 = -3 + 2i; z4 = -1 – i.
Решение:

а
в
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число  = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·
= a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·  = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
= a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
 .
.
Например, 
Самостоятельная работа
| 1 вариант | 2 вариант | Количество баллов |
| № 1. Изобразите на плоскости заданные комплексные числа: |
|
| z1= 4i | z1= -5i | 1 |
| z2 = 3 + i | z2= 4 + i | 1 |
| z3= - 4 +3i | z3 = -7 + 2i | 1 |
| z4= - 2 -5i | z 4= -3 – 6i | 1 |
| № 2. Произведите сложение и вычитание комплексных чисел: |
|
| А) (3 + 5i) + (7 – 2i).
б) (6 + 2i) + (5 + 3i). в) (– 2 + 3i) - (7 – 2i).
г) (5 – 4i) - (6 + 2i). | (3 – 2i) + (5 + i).
(4 + 2i) + (– 3 + 2i).
(– 5 + 2i) - (5 + 2i).
(– 3 – 5i) - (7 – 2i). | 2 2 2 2 |
| № 3. Произведите умножение комплексных чисел: |
|
| a) (2 + 3i)(5 – 7i).
б) (6 + 4i)(5 + 2i).
в) 11) (3 – 2i)(7 – i).
г) (– 2 + 3i)(3 + 5i). | (1 –i)(1 + i).
(3 + 2i)(1 + i).
(6 + 4i)3i.
(2 – 3i)(– 5i). | 2
2
2
2 |
| № 4. Выполните деление комплексных чисел: |
|
| а) б) | a)
б)
| 2 2
|
| № 5. Выполните действия: |
|
| a) (3 + 2i)(3 – 2i).
б) (5 + i)(5 – i).
в) (1 – 3i)(1 + 3i). | а) (7 – 6i)(7 + 6i).
б) (4 + i)(4 – i).
в) (1 – 5i)(1 + 5i). | 2 2 2 |
| № 6. Решите уравнения: |
|
| а) x2 – 4x + 13 = 0. б) x2 + 3x + 4 = 0
| а) 2,5x2 + x + 1 = 0.
б) 4x2 – 20x + 26 = 0.
| 3
3 |
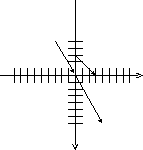
| №7. На рисунке показано графическое изображение комплексных чисел. Перерисуйте рисунок в тетрадь. Обозначьте комплексные числа как z1, z2, z3. Запишите соответствующие аналитические формы. |
|
| 
| 
| 2 |
Критерии оценки
| Набранное количество баллов | оценка |
| 21 – 28 баллов | 3 |
| 29 - 34 баллов | 4 |
| 35 - 38 балла | 5 |
Эталон ответа
| Вариант 1 | Вариант 2 |
|
| 1. |
|
| z1 z2 z3 z4 | z1 z2 z3 z4 | 1 1 1 1 |
| 2. |
|
| А) 10 + 3i Б) 11 + 5i В) -9 – 6i Г) -1 - 6i | А) 8 – i Б) 1 + 4i В)- 10 Г) -10 – 3i | 2 2 2 2 |
| 3. |
|
| А)10 + 3i Б)22 + 32i В)19 – 17i Г) -21 - i | А) 2 Б) 1 + 5i В)-12 + 18i Г) 10i - 15 | 2 2 2 2 |
| 4. |
|
| А)1 + i Б) – i
| А)1 – i Б)i
| 2 2 |
| 5. |
|
| А)13 Б)26 В)10
| А)85 Б)17 В)26
| 2 2 2
|
| 6. |
|
| А) 2 + 3i Б)1,5 + i
| А) – 0,2 + 0,6i Б)2,5 + 0,5i
| 3 3 |
| 7. |
|
| А)z1 = -3 + 5i Б)z2 = 3 + 3i В)z3 = 4 – 7i
| А)z1 = -7 + 3i Б)z2 = 2 + -5i В)z3 = -2 -7i
| 2 |
Критерии оценки
| Набранное количество баллов | Оценка |
| 21-28 | 3 |
| 29-34 | 4 |
| 35-38 | 5 |




















