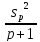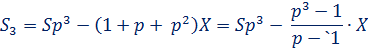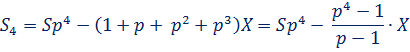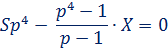Практикум по решению экономических задач

Одним из важнейших потребностей современной школы является воспитание делового человека, компетентного в сфере социально-трудовой деятельности, а также в бытовой сфере. Сегодня жизнь настоятельно требует, чтобы выпускник имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений.

Одной из особенностей вариантов ЕГЭ по математике в 2015 году является включение задачи № 19, в 2016 году – задание № 17, представляющего собой практико-ориентированную задачу. Среди задач с социально-экономическим содержанием важны называемые «банковские задачи», так как при ее решении можно столкнуться с различными банковскими операциями (вкладами, ссудами). Согласно статистике, почти каждая семья берет кредит на приобретение того или иного товара! В сегодняшние дни потребительские кредиты, кредитные карты, автокредиты, ипотека, вклады, банковские карты и другие финансовые услуги очень распространены и играет важную роль в экономике страны и каждой семьи.

Рассмотрим основные подходы к решению нового типа задач ЕГЭ по математике – задач с «экономическим содержанием», связанные с понятием «процент»

Задача 1.

31 декабря 2015 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?

РЕШЕНИЕ:

1. Пусть сумма кредита равна S = 4 290 000, а годовые составляют а = 14,5%.

2. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент равный р=1 + 0,01а.

3. После первой выплаты сумма долга составит s₁ = s_p -x

4.После второй выплаты сумма долга составит

s₂ = s _1p –x = (s_p - x)p – x = s_p² – (1 +p) x

5. По условию двумя выплатами Дмитрий должен погасить кредит полностью, поэтому s_p² – (1 +p) x = 0

x =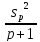

6. Откуда при S = 4290000 и а = 14,5, получаем: р = 1,145 и

Ответ: 2622050.

ЗАДАЧА 2:

31 декабря 2014 года Алексей взял в банке 6902000 рублей в кредит под 12,5% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

РЕШЕНИЕ:

1. Пусть сумма кредита равна S, а годовые составляют а %.

2. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент

р = 1 + 0,01a.

3. После первой выплаты сумма долга составит s₁ = s_p -x

4. После второй выплаты сумма долга составит

s₂ = s _1p –x = (s_p - x)p – x = s_p² – (1 +p) x

5. После третьей выплаты сумма оставшегося долга равна

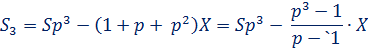
6. После четвертой выплаты сумма оставшегося долга равна

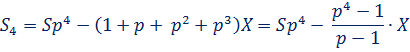
7. По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому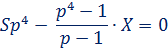

Откуда при S = 6902000 и а = 12,5, получаем: р = 1,125 и

Ответ: 2296350

ЗАДАЧА 3:

31 декабря 2014 года Владимир взял в банке некоторую сумму в кредит под 14% годовых. Схема выплаты следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга(то есть увеличивает долг на 14%), затем Владимир переводит в банк 4548600 рублей. Какую сумму взял Владимир в банке, если он выплатил долг двумя равными платежами (то есть за два года)?

РЕШЕНИЕ:

Пусть сумма кредита равна S, а годовые составляют а %.

Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент р= 1 + 0,01a.

После первой выплаты сумма долга составит

После второй выплаты сумма долга составит

По условию Владимир погасил кредит полностью за два года, поэтому

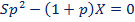
Х= 4548600 и а=14, получим р = 1.14 получим

Ответ: 7490000.

ЗАДАЧА 4

31 декабря 2014 года Георгий взял в банке кредит 1 млн рублей в кредит. Схема выплаты кредита следующая – 31 декабря каждого года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на а%), затем Георгий переводит очередной транш. Георгий выплатил кредит за два транша, переведя в первый раз 570 тыс рублей, во второй599,4 тыс рублей. Под какой процент банк выдал кредит Георгию?

РЕШЕНИЕ:

Пусть сумма кредита равна S, а годовые составляют а %.

Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент р= 1 + 0,01a.

После первой выплаты сумма долга составит

Исходя из условия после первой выплаты долг Георгия будет равен

После второй выплаты сумма долга составит

или

 При условии, что кредит был погашен за два транша это сумма должна равняться 0.

Получим уравнение

Отсюда а=11%.

Ответ: 11%.

ЗАДАЧА 5:

1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая - 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

РЕШЕНИЕ:

Заметим, что за 4 месяца Александр Сергеевич выплатит

275 000∙4= 1,1 млн рублей.

Таким образом, он не покроет долг с процентами.

Каждый месяц долг увеличивается не более, чем на

1100000∙ 0,01 = 11000 рублей.

Значит, за пять месяцев Александр Сергеевич должен будет выплатить не более

1100000 + 5∙11000 = 1155000 рублей,

что менее, чем

5∙ 275000 = 1375000 рублей.

Таким образом, Александр Сергеевич сможет выплатить кредит за 5 месяцев.

ЗАДАЧА 6:

Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк ¾ от всей суммы, которую он должен был банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

РЕШЕНИЕ:

Пусть фермер взял кредит S руб. под p% годовых.

Через год он должен банку S(1+0,01р) руб.

Через год фермер в счет погашения кредита вернул в банк ¾ от всей суммы, которую он должен был банку к этому времени, следовательно, ему осталось вернуть 0,25 S(1+0,01р) руб.

Еще через год он должен банку

(0,25 S(1+0,01р)) (1+0,01р) =0,25S(1+0,01р)² руб.

В счет полного погашения кредита он внес в банк сумму на 21% превышающую величину полученного кредита, то есть внес 1,21 S руб.

Получили уравнение: 0,25S(1+0,01р)²=1,21 S.

(1+0,01р)²=4,84

1+0,01р=2,2

p=120% Ответ: 120

ЗАДАЧА 7:

Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?

Предложение «Суммы, выплачиваемые в конце каждого месяца, …то есть на одну и ту же величину» означает: Сергей взятую сумму возвращал равными долями.

Общая сумма, уплаченная Сергеем банку сверх кредита, обусловлена только применением процентной ставки.

В первом месяце эта часть заплаченной суммы составляла 0,12S, во втором - в третьем - , …..в восьмом - ,наконец, в

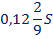
последнем -

 Всего за 9 месяцев:

Искомое процентное отношение есть 60

ЗАДАЧА 8:

Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.

РЕШЕНИЕ:

Пусть сумма кредита S, процентная ставка банка х%. Предложение «Суммы, выплачиваемые в конце каждого месяца, ….уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями.

Сумма, образованная применением процентной ставки, составляет:

Общая сумма, выплаченная Антоном за 6 месяцев:

А эта сумма по условию задачи равна .

Решим уравнение:

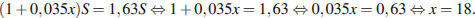
Ответ: 18.