| Сборник задач по геометрии |
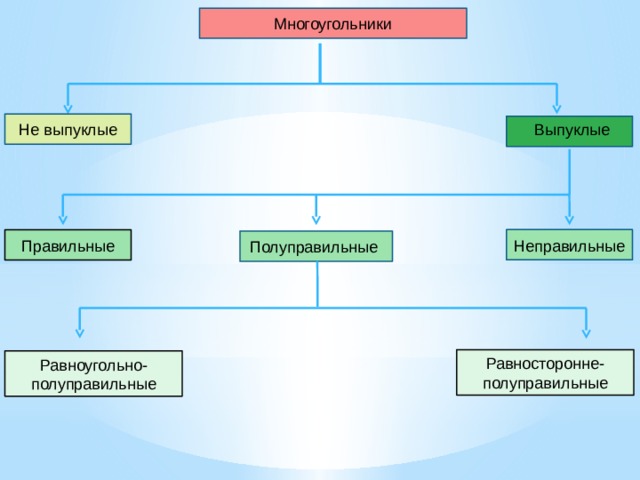
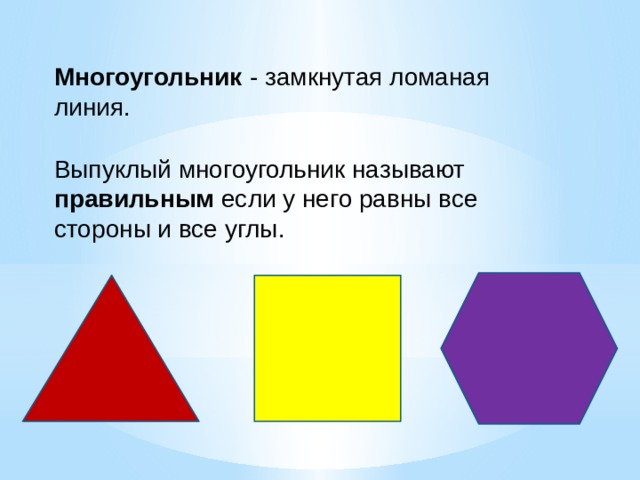
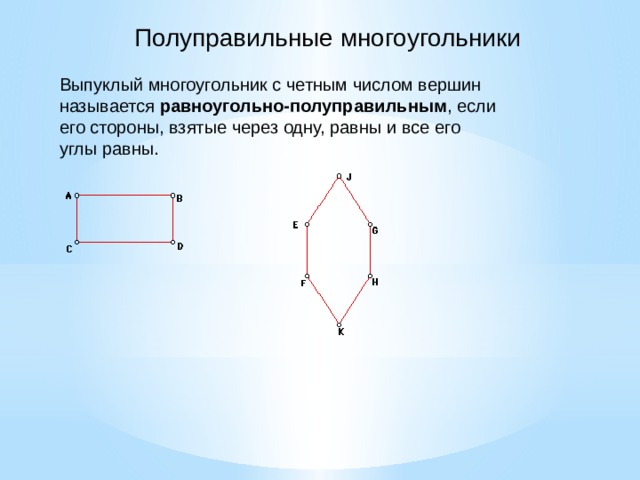
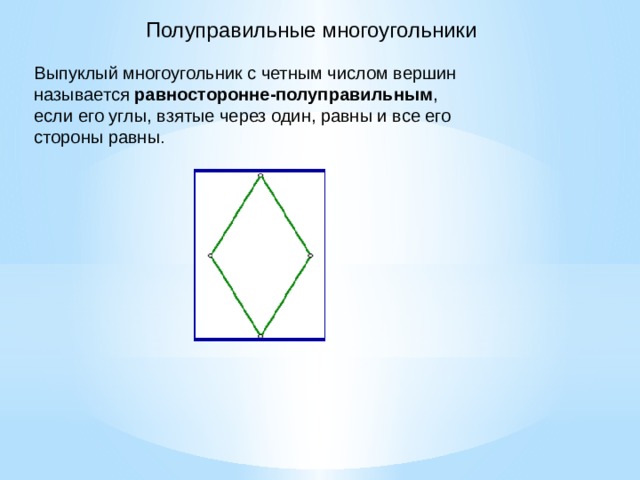
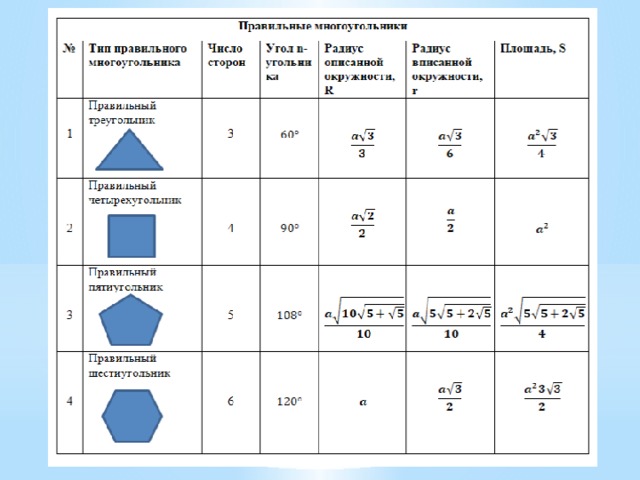
| Правильные многоугольники |
|
|
Содержание
| Вариант 1 | 2-3 |
| Вариант 2 | 4-5 |
| Вариант 3 Правильные многоугольники на ОГЭ | 6-7 8-14 |









Правильные многоугольники на ОГЭ
1. Задание 17 № 311503
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

2. Задание 17 № 311507
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

3. Задание 17 № 369806
Радиус окружности, описанной около квадрата, равен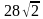 . Найдите длину стороны этого квадрата.
. Найдите длину стороны этого квадрата.
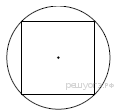
4. Задание 17 № 369835
Радиус окружности, описанной около квадрата, равен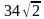 . Найдите длину стороны этого квадрата.
. Найдите длину стороны этого квадрата.

1. Задание 18 № 348712
Найдите площадь квадрата, описанного около окружности радиуса 7.

2. Задание 18 № 349407
Найдите площадь квадрата, описанного около окружности радиуса 25.

3. Задание 18 № 349720
Найдите площадь квадрата, описанного около окружности радиуса 9.

4. Задание 18 № 352414
Найдите площадь квадрата, описанного около окружности радиуса 16.

5. Задание 18 № 353229
Найдите площадь квадрата, описанного около окружности радиуса 14.

1. Задание 25 № 181
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.

2. Задание 25 № 315039
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.

3. Задание 25 № 315047
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.

4. Задание 25 № 315124
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.

1. Сторона равностороннего треугольника равна 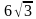 . Найдите радиус окружности, описанной около этого треугольника.
. Найдите радиус окружности, описанной около этого треугольника.
2. Сторона равностороннего треугольника равна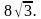 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.

3. Сторона равностороннего треугольника равна 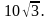 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.

4. Сторона равностороннего треугольника равна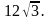 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.

5. Сторона равностороннего треугольника равна 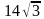 . Найдите радиус окружности, описанной около этого треугольника.
. Найдите радиус окружности, описанной около этого треугольника.

5. Сторона равностороннего треугольника равна 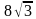 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.
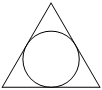
6. Сторона равностороннего треугольника равна 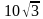 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.

7. Сторона равностороннего треугольника равна 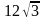 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.

8. Сторона равностороннего треугольника равна 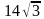 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.

9. Сторона равностороннего треугольника равна 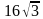 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.

10. Радиус окружности, вписанной в равносторонний треугольник, равен 15. Найдите высоту этого треугольника.
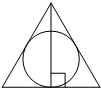
11. Радиус окружности, вписанной в равносторонний треугольник, равен 18. Найдите высоту этого треугольника.

12. Радиус окружности, вписанной в равносторонний треугольник, равен 14. Найдите высоту этого треугольника.

13. Радиус окружности, вписанной в равносторонний треугольник, равен 8. Найдите высоту этого треугольника.

14. Радиус окружности, вписанной в равносторонний треугольник, равен 8. Найдите высоту этого треугольника.

15. Биссектриса равностороннего треугольника равна  Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
16. Высота равностороннего треугольника равна  . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
17. Медиана равностороннего треугольника равна  Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
18. Биссектриса равностороннего треугольника равна  Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
19. Высота равностороннего треугольника равна  . Найдите сторону этого треугольника.
. Найдите сторону этого треугольника.
8






















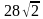 . Найдите длину стороны этого квадрата.
. Найдите длину стороны этого квадрата.
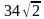 . Найдите длину стороны этого квадрата.
. Найдите длину стороны этого квадрата.




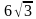 . Найдите радиус окружности, описанной около этого треугольника.
. Найдите радиус окружности, описанной около этого треугольника.
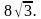 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.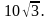 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.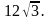 Найдите радиус окружности, описанной около этого треугольника.
Найдите радиус окружности, описанной около этого треугольника.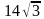 . Найдите радиус окружности, описанной около этого треугольника.
. Найдите радиус окружности, описанной около этого треугольника.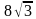 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.
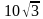 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.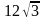 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.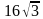 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.