План-конспект открытого урока по теме: «Преобразование плоскости: поворот».
Ершова Ирина Васильевна учитель математики
Предмет: геометрия.
Класс: 9.
Тема: Параллельный перенос и поворот
Тип урока: изложение нового материала.
Цели урока:
Образовательная: сформировать представление о повороте как виде движения и отработать пошагово способ построения простейших геометрических фигур;.
Воспитательная: воспитывать трудовые навыки; стимулировать любознательность и творческое начало.
Развивающая: развивать общеучебные навыки анализа, синтеза, классификации, устной речи, самостоятельной работы, работы в группах и коллективе, зрительного представления, творческого воображения, ориентировки в пространстве.
Задачи урока:
- добиться усвоения понятия поворота как вида движения;
- добиться умения получать фигуру путем поворота в случае простейших фигур: точки, отрезка, треугольника;
- продемонстрировать применение указанных преобразований к решению задач.
Оборудование и пособия: интерактивная доска, карточки для групповой работы, заготовленные слайды, видеопроектор, транспортиры, чертежные инструменты;
«пиратский» инвентарь: пиратская шляпа, повязка на глаз, бандана, слайд с «картой сокровищ» .
Этапы урока.
| 1. Целеполагание. |
| 2. Актуализация опорных понятий. |
| 3 Повторение пройденного материала с последующей самопроверкой. |
| 4. Изложение нового материала.. |
| 5. Тренировочное закрепление. |
| 6. Физкультминутка «поворот» |
| 7. Связь с другими науками. |
| 8. Рассмотрение творческой задачи-инсценировки. |
| 9. Подведение итогов. |
Ход урока.
1.Целеполагание.
Обратиться к ученикам: «Повернитесь друг к другу и посмотрите друг на друга. Каким словом можно назвать это действие?». «Поворот». – «Вы уже догадались, о чем пойдет речь сегодня на уроке?»
Формулировка и запись темы урока.
- Мы все встречаемся с этим понятием в жизни, а сегодня наша цель – узнать, что такое поворот в научном математическом понимании и научиться осуществлять поворот простейших геометрических фигур.
2. Актуализация опорных понятий.
Что мы в математике называем движением? .( Движение – это такое преобразование плоскости на себя, при котором сохраняются расстояния между точками).
Что является показателем того, что произведенное преобразование является именно движением? – Сохранение расстояний между точками.
.
Рассмотрим на примерах, является ли в каждом случае преобразование движением? Сохраняется ли расстояние между точками?






3. Повторение пройденного материала.
Какое преобразование, являющееся движением, мы уже умеем выполнять? – Параллельный перенос.

Теперь, давайте вспомним, как мы этим определением можем воспользоваться, когда нам, скажем, предстоит перенести треугольник. Ведь, согласно, определению, нужно перенести каждую его точку, как же это возможно сделать?
- Достаточно перенести три точки его концов, т.к. по двум концам можно получить только один отрезок.
Вспомним, как мы умеем это делать? С помощью слайдов проговорим устно этапы построения параллельного переноса в этом случае.
Итак, дан треугольник и указан вектор переноса.
Дано:
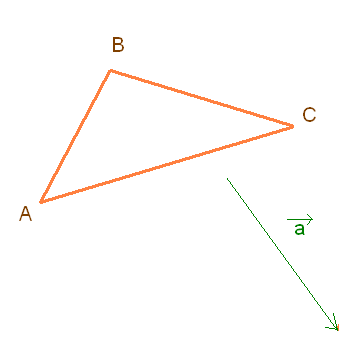
Этапы построения переноса:
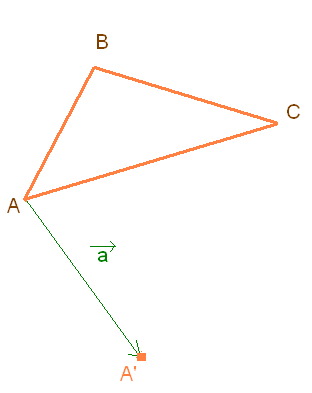
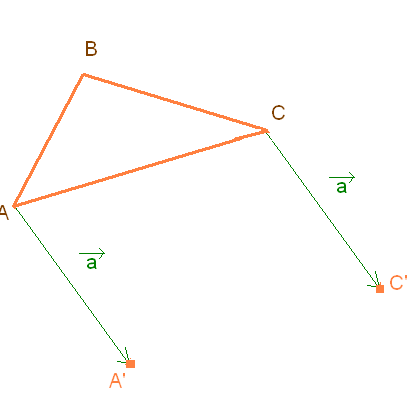
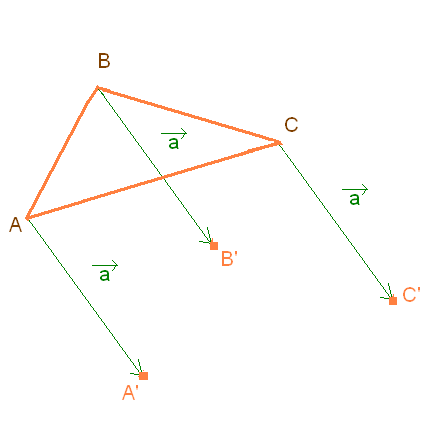
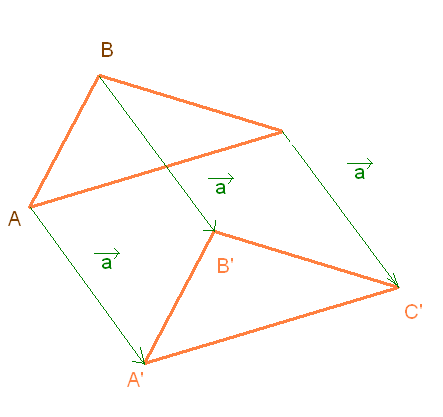
4. Изложение понятия «поворот».
Ну, а теперь мы продолжим знакомство с видами движения и переходим к следующему из них, о котором сказали в начале урока, а именно, к повороту.
4.1. Подведение к понятию «поворот».
Рассмотрим примеры поворота.

- Что здесь поворачивается?
- Стрелка.
-Какое направление поворота?
-По часовой стрелке.
- Что является центром поворота?
- Середина часов.
- На какой угол я повернула стрелку? (15 мин, 30мин, 45 мин, ровно)
- На 90˚, 180˚, 270˚, 360˚.
4.2 Примеры поворота в повседневной жизни.
Рассмотрим еще примеры поворота. Определите в них центр и направление.




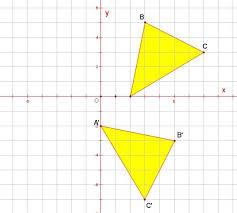



4. 3 Теория поворота
Поворот
Поворотом плоскости вокруг точки О на угол ά называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, ОМ=ОМ1 и угол МОМ1 равен ά.
ДАНО:
Угол ά, точка М, центр поворота – точка О.
ПОСТРОЕНИЕ:
Поворот является движением, т. е. отображением плоскости на себя, сохраняющим расстояния.
Выполняем поворот точки с проговариванием каждого этапа. По выполнении работы учащимся предлагается повторно проговорить шаги построения.
5. Тренировочное закрепление.
5.1 Поворот отрезка, когда центр поворота совпадает с одним из его концов.
Допустим, нам требуется повернуть отрезок. Как мы можем повернуть каждую его точку, ведь их бесконечно много?
- Надо повернуть его концы.
- А остальные точки тоже повернутся? Можно ли это как-нибудь доказать?
- По аксиоме: через две точки проходит единственная прямая.
- А если речь пойдет о треугольнике или другой фигуре, состоящей из отрезков?
- Тогда надо повернуть вершины, т.е. концы отрезков.
Переходим к тренировке.
Дан отрезок. Центр поворота совпадает с одним из его концов. Задание: повернуть отрезок на заданный угол вокруг заданного центра. Следует слайд с анимацией.
- Что произошло с точкой О? – Перешла в саму себя.
-Остается теперь повернуть точку А, а как это делать вы только что видели. Свернуть кадр с результатом.
- Задание: воспроизведите в тетради результат. Снова развернуть кадр с результатом, выполняется самопроверка.
На том же чертеже выполним поворот в другую сторону: против часовой стрелки. Пока идет выполнение задания, раздаю листы для группового задания и маркеры тем, кто справился в первую очередь Группы приступают к выполнению задания, с остальными и теми, у кого есть вопросы, разбираем это задание и проговариваем определение, шаги построения.
5.2 Работа в группах.
Задание усложняется. Требуется выполнить поворот отрезка на заданный угол с заданным центром, не совпадающим ни с каким из его концов. (Задание одно на группу из 4-х человек).
4 группы.
1 группа 2 группа
3 группа 4 группа
Проверка. Сравниваем отрезки, полученные 1 и 2 группами; 3 и 4 группами- они должны быть одинаковыми ( одинаковая длина и параллельны), т.к. это поворот одного и того же отрезка дважды на угол 90˚.
6. Физкультминутка «поворот»
Итак, продолжаем изучать поворот. Ну, как его можно изучать, ни разу не повернувшись?
Давайте встанем. Учитель говорит: « Внимание, поворот: 90 градусов вправо. Внимание, поворот: 180 градусов влево. И снова влево на 360 градусов. А теперь на 360 градусов вправо. А теперь повторим снова…». Заодно, повторили «право-лево».
7.Связь с другими науками
- Посмотрите на этот цветок, какой он очаровательный. Но его очарование не просто интуитивно, оно подчиняется математическим законам. Давайте посмотрим на него сверху.
Видите: никакой лист не располагается один под другим, а как растет каждый следующий лист?
- Повернут по отношению к другому на какой-то угол.
- Вокруг какого центра?
- Вокруг стебля.
- А для чего так в природе устроено, зачем каждый следующий лист повернут на один и тот же угол?
- Чтобы был доступ солнца к каждому следующему листу и осуществлялся процесс фотосинтеза.
А теперь предлагаю вашему вниманию стихотворение известного русского ученого М.В. Ломоносова, в котором он гениальным примером указывает ответ на известный научный спор. О каком же споре идет речь?
Случилось вместе два астронома в пиру,
И спорили весьма между собой в жару.
Один твердил: Земля, вертясь, круг Солнца ходит;
Другой – что солнце все с собой планеты водит;
Один Коперник был, другой слыл Птолемей.
Тут повар спор решил усмешкою своей.
Хозяин спрашивал: - Ты звезд теченье знаешь?
Скажи, как ты о сем сомненье рассуждаешь?
Он дал такой ответ: - Что в том Коперник прав,
Я правду докажу, на Солнце не бывав.
Кто видел простака из повара такого,
Который бы вертел очаг кругом жаркого?
Речь идет о столкновении теорий геоцентрической (гео – земля) и гелиоцентрической (гелиос – земля). Применяя к нашему уроку, мы можем сказать, что этот спор шел о центре поворота.
-Кто знает основоположников той и другой теорий?
-«Геоцентрическая» – Клавдий Птолемей; «гелиоцентрическая» – Коперник.
Итак, какие примеры поворота мы здесь наблюдаем? Вокруг какого центра происходит этот поворот?
-На какой угол поворачивается земля за 1 сезон? Подсказка: это четверть оборота.
-На 90˚.
-А за полгода?
-На 180˚
-За год?
-На 360˚.
8. Рассмотрение творческой задачи-инсценировки.
Ну, и под конец нас ждет один приключенческий сюжет, но будьте внимательны; в нем вы должны распознать задачу. Поэтому приготовьте карандаши и линейки по ходу сюжета вы должны будете сделать необходимый к задаче чертеж, который потом будем обсуждать.
Инсценировка. Два подготовленных ученика надевают инвентарь: старый пират – повязку на глаза и пиратскую шляпу, другой – молодой пират Джо – бандану.
СТАРЫЙ ПИРАТ:
Поди сюда, Джо. Ты знаешь, зачем я тебя сюда позвал? Я уже старый пират и чувствую, что дни мои сочтены, поэтому я хочу открыть тебе тайну. Ты знаешь, на что я потратил все последние годы? На поиски клада. Ценою жизни я раздобыл карту, где указано, как найти лад. Вот она (на самом деле там не карта, а текст задачи). Прочти, что там написано.
Джо разворачивает «карту», читает медленно, чтоб все смогли начертить чертеж.
Где зарыт клад.
На берегу острова имеется дуб D , берёза B , вкопанный флаг F. От F надо пройти к D , считая шаги, повернуть направо( строгий поворот направо - 90˚ ), пройти столько же и вбить кол K1, от F дойти до B , повернуть налево, пройти столько же, вбить кол K2. Точно посредине между кольями рыть.
ДЖО.
Так если у тебя эта карта, почему ты до сих пор не раскопал клад?
СТАРЫЙ ПИРАТ.
Вот в этом и вся проблема. Когда я приплыл на этот остров, флага там не оказалось. (Встают). Джо, я поручаю тебе это дело. Ты должен, должен найти этот клад. (Уходят.).
Ну что, поможем Джо найти клад? Сначала проверим, такой ли у вас вышел чертеж?
Решение.
К1 переходит в F путем поворота на 90˚ с центром в точке D;
F переходит в К2 путем поворота на 90˚ с центров в точке В.
Таким образом, К1 переходит в К2 в результате двух поворотов (композиции) вокруг точек D и В; точка Х – центр симметрии. Важный вывод: этот же центр симметрии можно получить и другим путем, минуя точку F, а именно: отобразить любую другую точку путем этих же двух поворотов: вокруг точек D и В на 90˚. Удобно взять уже имеющуюся точку. Какие ваши предложения? Возьмем точку D.
Повернем её вокруг неё же самой на 90˚ – какую точку получим? – Опять D.
Повернём её вокруг точки В на 90˚. Это надо построить.
Получение точки К. (Это не та же точка, что и К2). Соединяем точки D и К и делим данное расстояние пополам. Получаем точку Х.
9. Подведение итогов.
Перед вами набор математических понятий. Выберите те понятия, с которыми мы работали сегодня на уроке.
Луч, симметрия, движение, биссектриса, расстояния, плоскость, перпендикуляр, высота, поворот, отображение.
Для проверки: выбранных слов должно получиться 5.
А теперь свяжите их в одно предложение. (При правильном выполнении задания должно получиться определение поворота). Если у вас получилось определение поворота, значит, вы сегодня на уроке его усвоили.





































