Презентация "Активные методы обучения математике"

Активные методы обучения математике

Подготовила Колесова И. В.

МБОУ БГО СОШ №13

2019-2020 ученый год

Что такое АМО?

• Активные методы обучения - методы, стимулирующие познавательную деятельность обучающихся.

АМО строятся:

• в основном на диалоге, предполагающем свободный обмен мнениями о путях разрешения той или иной проблемы
• на практической направленности, игровом действие и творческом характере обучения;
• интерактивности, разнообразных коммуникациях,
• на использовании знаний и опыта обучающихся, групповой форме организации их работы,
• деятельностном подходе к обучению, движении и рефлексии.

Примеры методов активного обучения 

• Мозговой штурм
• Групповое решение проблемы
• Работа в малых группах
• Ролевое моделирование и деловые игры
• Дискуссия
• Занятие – брифинг
• Занятие – праздник
• Бинарная лекция
• Метод «Синквейн»
• Метод рецензирования
• Кейс-метод

Мозговой штурм

• Метод решения проблемы на основе стимулирования творческой активности, при котором участникам обсуждения предлагают высказывать как можно большее количество вариантов решения, в том числе самых фантастичных. 
• 27 · 12 + 63 ·12 = (27 + 63) · 12 = 90 · 12 = 1080
• 27 · 12 + 63 ·12 = 90 · 12 = 90 · 10 + 90 · 2 = 900+180 = = 1080
• 27 · 12 + 63 · 12 = 324 + 756 = 1080
• 27 · 12 + 63 · 12 = 27 · 10 + 27 · 2 + 63 · 10 + 63 · 2 =

= 270 + 54 + 630 + 126 = 900 + 180 = 1080

Групповое решение проблемы

• Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
•  

Поставщик

Цена бруса (руб. за 1 м 3 )

A

4200

Б

Стоимость доставки

В

10200

4800

Дополнительные условия

4300

8200

При заказе на сумму больше 150 000 руб. доставка бесплатно

8200

При заказе на сумму больше 200 000 руб. доставка бесплатно

• При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1 600 рублей, щебень стоит 780 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?
• Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерсти синего цвета. Можно купить синюю пряжу по цене 60 рублей за 50 г, а можно купить неокрашенную пряжу по цене 50 рублей за 50 г и окрасить ее. Один пакетик краски стоит 10 рублей и рассчитан на окраску 200 г пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.

• Заметно повышают интерес учащихся математические кроссворды, ребусы.
• Неизменным успехом пользуется у школьников конкурс "Художников", который можно проводить при изучении координатной плоскости. По заданным координатам ребята выстраивают различные изображения.

• Или обратная задача. Рисуют фигуру в координатной плоскости ( фигуру придумывают сами ) и задают координаты точек, чтоб можно эту фигуру было построить.

• По вертикали: 1. Царица наук
• По горизонтали: Математический кроссворд
• 1. Знак математического действия.
• 2. Единица измерения углов.
• 3. Куб числа 10.
• 4. Фамилия автора учебника
• по математике.
• 5. Единица длины.
• 6. Вид дроби.
• 7. Единица массы.
• 8. Прибор для построения окружности
• 9. Прямоугольник с равными сторонами.
• 10. Число, записанное под чертой дроби.

• Заметно повышают интерес учащихся математические кроссворды, ребусы

1

2

3

4

5

6

7

8

9

10

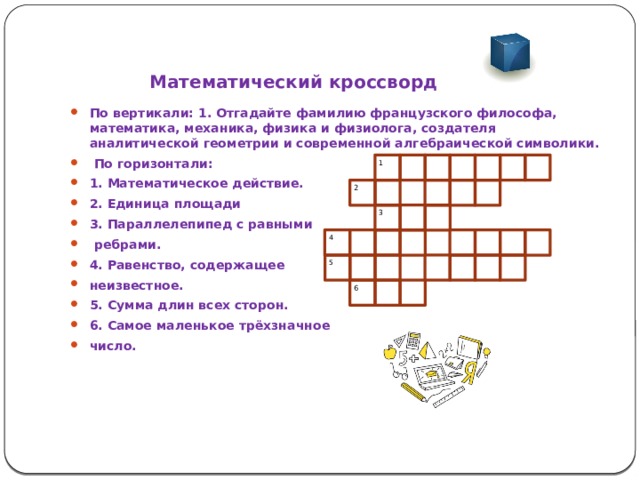
Математический кроссворд

• По вертикали: 1. Отгадайте фамилию французского философа, математика, механика, физика и физиолога, создателя аналитической геометрии и современной алгебраической символики.
• По горизонтали:
• 1. Математическое действие.
• 2. Единица площади
• 3. Параллелепипед с равными
• ребрами.
• 4. Равенство, содержащее
• неизвестное.
• 5. Сумма длин всех сторон.
• 6. Самое маленькое трёхзначное
• число.

1

2

3

4

5

6

Приём «Кластер»

•   Использование приёма «Кластер» на уроках математики формирует и развивает умения выделять существенные (важные) признаки предмета, умения сравнивать несколько предметов (геометрических фигур), отмечая при этом сходные и различные признаки и свойства, умения сделать несложные обобщения на основе выделенных общих свойств предметов. Этот приём является одним из основных для формирования и развития мыслительных операций (анализ и синтез), а также умения строить обоснованные (логичные) рассуждения.

Последовательность действий по составлению кластера

• Посередине чистого листа (классной доски) пишут ключевое слово или предложение, которое является ключевым в раскрытии идеи, темы;
• Вокруг записывают слова или предложения, выражающие идеи, факты, образы, подходящие для данной темы;
• По мере записи появившиеся слова соединяют прямыми линиями с ключевым понятием. У каждого из «спутников» в свою очередь тоже появляются «спутники», устанавливаются новые логические связи.

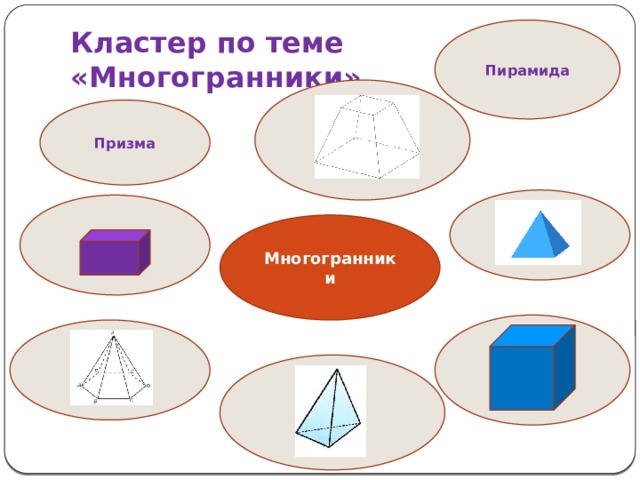
Кластер по теме «Многогранники»

Пирамида

Призма

Многогранники

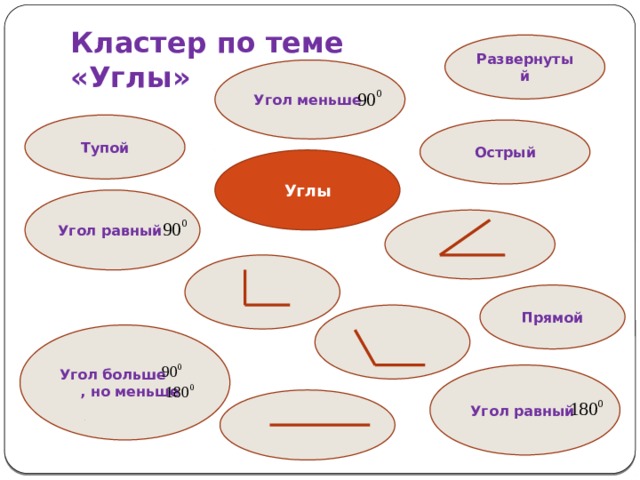
Кластер по теме «Углы»

Развернутый

Угол меньше

Тупой

Острый

Углы

Угол равный

Прямой

Угол больше , но меньше

Угол равный

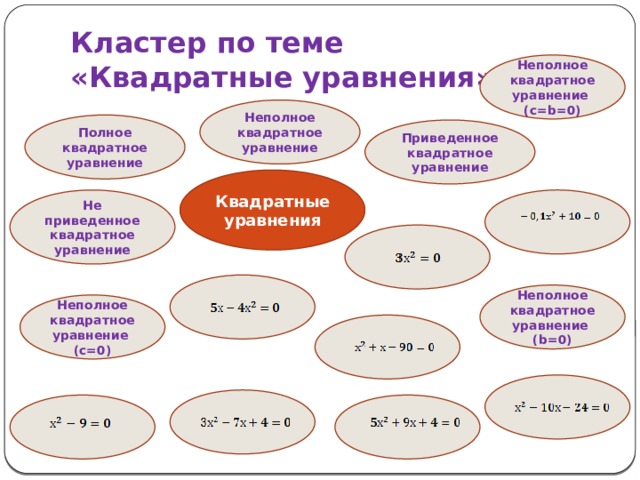
Кластер по теме «Квадратные уравнения»

Неполное квадратное уравнение (с=b=0)

Неполное квадратное уравнение

Полное квадратное уравнение

Приведенное квадратное уравнение

Квадратные уравнения

Не приведенное квадратное уравнение

Неполное квадратное уравнение (b=0)

Неполное квадратное уравнение (с=0)

Треугольники

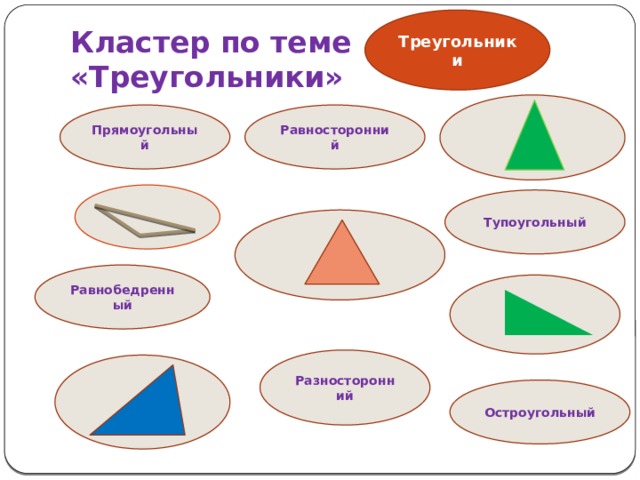
Кластер по теме «Треугольники»

Равносторонний

Прямоугольный

Тупоугольный

Равнобедренный

Разносторонний

Остроугольный

Метод рецензирования

• Умение увидеть свою ошибку, указать её причину и исправить всегда приводит к возрастанию активности учащихся на уроке.
• Например, при решении уравнения, умышленно допускаю ошибку, а потом предлагаю её найти и исправить.

Кейсовые технологии

• Усовершенствованный метод анализа конкретных ситуаций, метод активного проблемно-ситуационного анализа, основанный на обучении путём решения конкретных задач – ситуаций. Обучающиеся должны проанализировать ситуацию, разобраться в сути проблем, предложить возможные решения и выбрать лучшее из них.

Пример кейса

• Вы – маляр, которому предстоит покрасить комнату длиной 7 метров, шириной 4 метра и высотой 3 м. Пользуясь приведёнными ниже данными, спланируйте свои действия и представьте свой план на утверждение.
• Размер комнаты : длина 8 метров, ширина 4 метра и высота 3 м.
• В наличии : 4 кг банок краски.
• Расход краски на 1   :  250 г.
• Из этого кейса учащиеся самостоятельно выводят проблему – не можем покрасить комнату, так как не знаем, сколько потребуется краски и будет ли имеющихся банок достаточно. Выведут цель. Далее идёт разбиение этой цели на задачи.
• 1. Узнать, сколько литров краски уйдёт на покраску всей комнаты.

Не хватает данных: площадь всей комнаты.

• 1.1 Рассчитать площадь всей комнаты.

= 72 - площадь всей комнаты.

• 1.2 Рассчитать, сколько уйдёт литров краски.

= 18 кг – уйдёт на покраску комнаты.

• 2. Выяснить, достаточно ли имеющегося количества .
• Имеется 4 пятилитровых банки, то есть 20 кг. Нужно 18 кг.
• Вывод: банок достаточно, и придётся использовать все имеющиеся банки, причём последняя останется незаконченной.

Преимущества использования активных методов обучения

• Повышают эффективность усвоения материала
• Повышают мотивацию учащихся
• Позволяют максимально учитывать индивидуальные особенности учащихся
• Возможно применение с любой возрастной группой
• Позволяют решать не только образовательные, но и воспитательные задачи
• Развивают психологические компетенции учащихся