Презентация "Четырёхугольники"

Четырехугольники

Фролова Ольга Александровна, учитель математики

МБОУ «Караваевская СОШ»

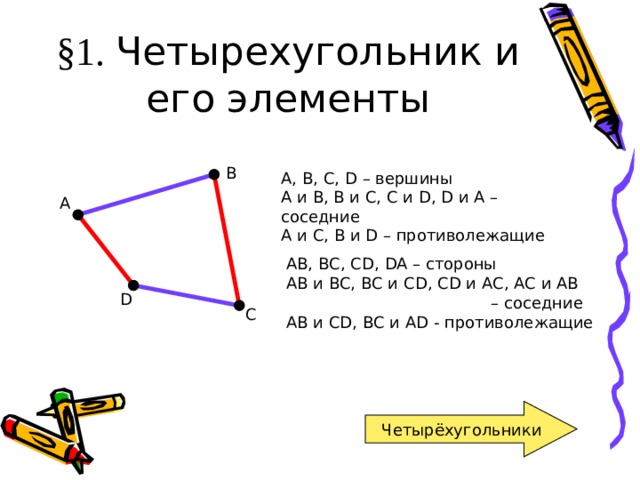
§ 1. Четырехугольник и его элементы

В

А, В, С, D – вершины

А и В, В и С, С и D , D и А – соседние

А и С, В и D – противолежащие

А

АВ, ВС, С D , DA – стороны

АВ и BC , ВС и CD , С D и АС, АС и АВ

– соседние

АВ и С D , В C и AD - противолежащие

D

С

Четырёхугольники

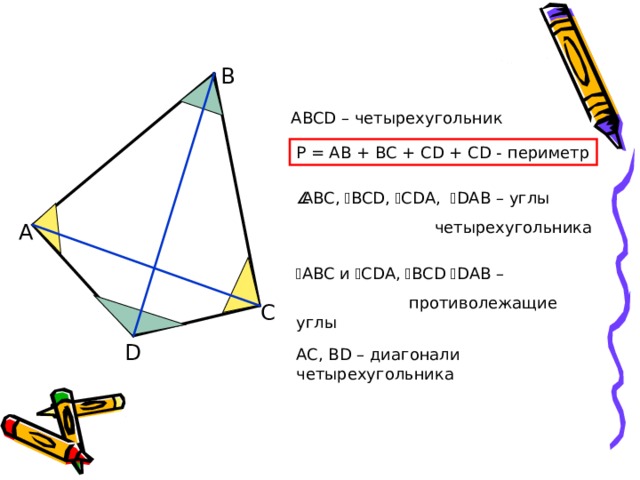
В

ABCD – четырехугольник

P = AB + BC + CD + CD - периметр

 ABC ,  BCD ,  CDA ,  DAB – углы

четырехугольника

А

 ABC и  CDA ,  BCD  DAB –

противолежащие углы

С

D

AC , В D – диагонали четырехугольника

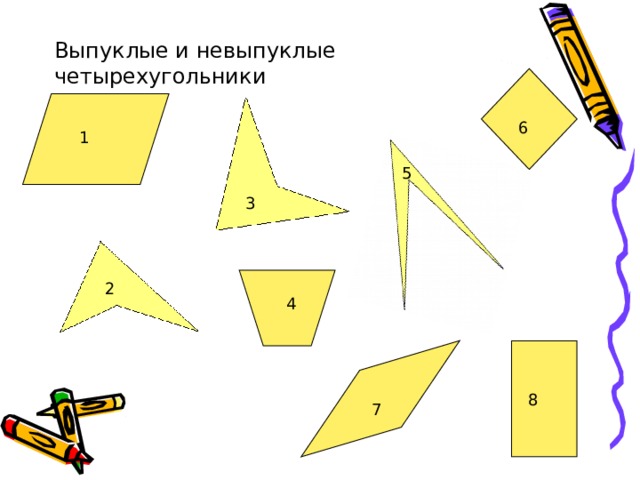
Выпуклые и невыпуклые четырехугольники

6

1

5

3

2

4

8

7

Теорема 1.1

Сумма углов четырехугольника равна 360 º .

Следствие

В четырехугольнике только один из углов может быть больше развёрнутого.

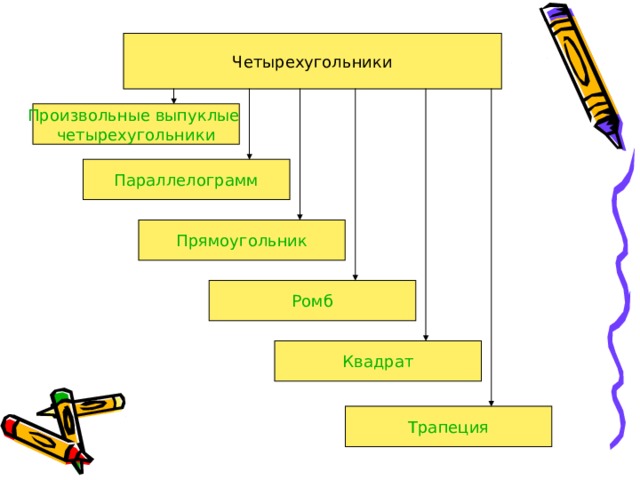
Четырехугольники

Произвольные выпуклые

четырехугольники

Параллелограмм

Прямоугольник

Ромб

Квадрат

Трапеция

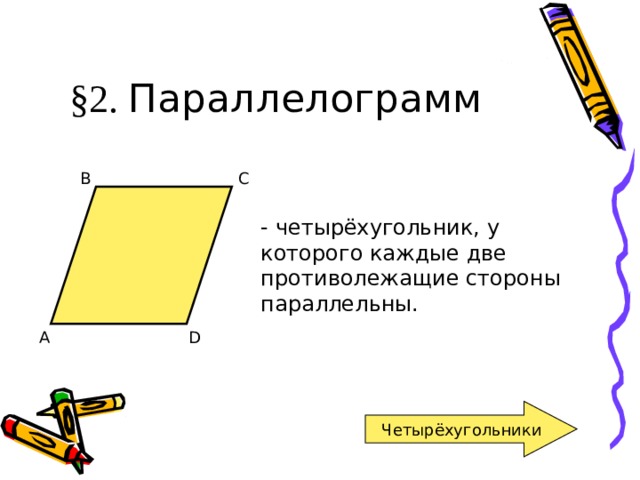
§ 2. Параллелограмм

В

С

- четырёхугольник, у которого каждые две противолежащие стороны параллельны.

А

D

Четырёхугольники

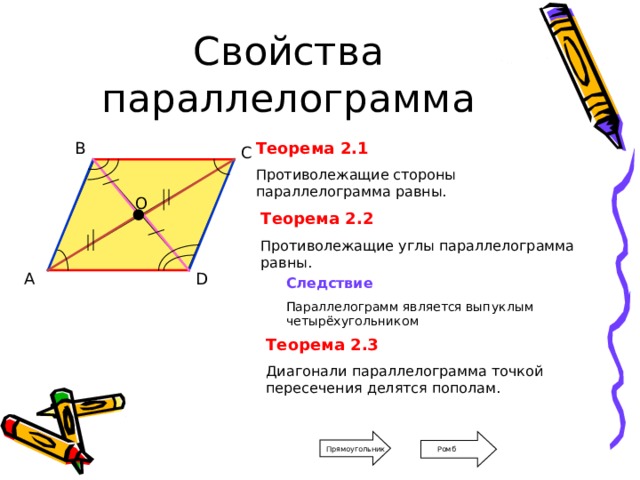
Теорема 2.1

B

Противолежащие стороны параллелограмма равны.

C

O

Теорема 2.2

Противолежащие углы параллелограмма равны.

A

D

Следствие

Параллелограмм является выпуклым четырёхугольником

Теорема 2.3

Диагонали параллелограмма точкой пересечения делятся пополам.

Прямоугольник

Ромб

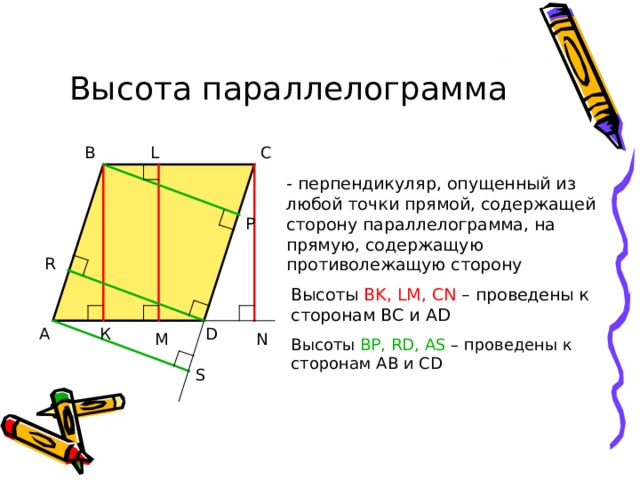
Высота параллелограмма

С

L

В

- перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону

P

R

Высоты BK , LM , CN – проведены к сторонам ВС и AD

Высоты BP , RD , AS – проведены к сторонам A В и CD

К

D

А

M

N

S

§ 3. Признаки параллелограмма

Теорема 3.1 (обратная теореме 2.1)

Если в четырёхугольнике каждые две противолежащие стороны равны, то этот четырёхугольник – параллелограмм.

Теорема 3.2

Если в четырёхугольнике две противолежащие стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Теорема 3.3 (обратная теореме 2.3)

Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Параллелограмм

Свойства

Признаки

Противолежащие стороны параллелограмма равны.

Если в четырёхугольнике каждые две противолежащие стороны равны , то этот четырёхугольник – параллелограмм.

Противолежащие углы параллелограмма равны.

Если в четырёхугольнике две противолежащие стороны равны и параллельны , то этот четырёхугольник – параллелограмм.

Диагонали параллелограмма точкой пересечения делятся пополам.

Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Ключевые задачи

• Докажите, что длина любой стороны четырёхугольника меньше суммы длин трёх остальных его сторон.
• Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке.
• Докажите, что сумма любых двух соседних углов параллелограмма равна 180 º (№43).
• Докажите, что угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма (№69).
• Докажите, что угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма (№70).
• Докажите, что если в четырёхугольнике каждые два противолежащих угла равны, то этот четырёхугольник – параллелограмм.
• Докажите, что если сумма углов, прилежащих к любой из двух соседних сторон четырёхугольника, равна 180 º , то этот четырехугольник – параллелограмм (№90).
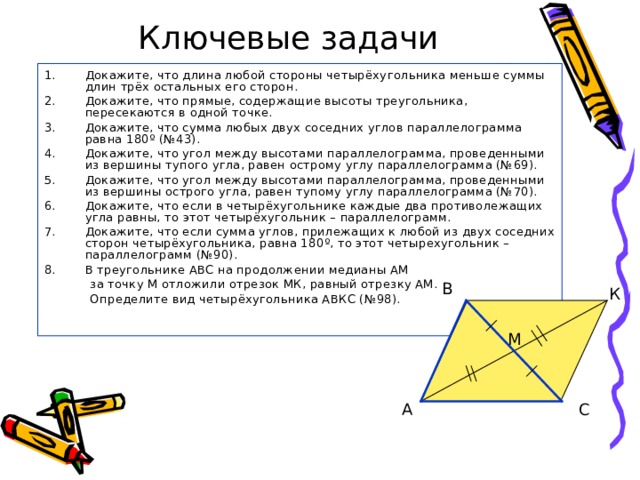
• В треугольнике АВС на продолжении медианы АМ

за точку М отложили отрезок МК, равный отрезку АМ.

Определите вид четырёхугольника АВКС (№98).

В

К

М

С

А

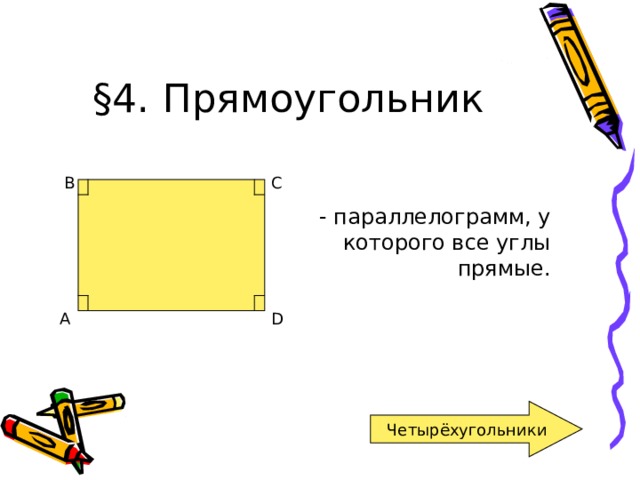
§ 4. Прямоугольник

С

В

- параллелограмм, у которого все углы прямые.

А

D

Четырёхугольники

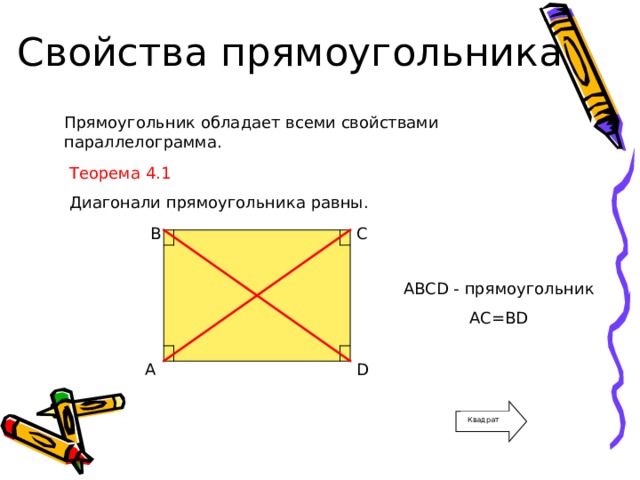
Свойства прямоугольника

Прямоугольник обладает всеми свойствами параллелограмма.

Теорема 4.1

Диагонали прямоугольника равны.

С

В

ABCD - прямоугольник

AC=BD

D

А

Квадрат

Признаки прямоугольника

Теорема 4.2

Если один из углов параллелограмма прямой, то этот паралеллограмм – прямоугольник .

Теорема 4.3

Если диагонали параллелограмма равны, то этот паралеллограмм – прямоугольник .

Ключевые задачи

1. Докажите, что четырёхугольник, все углы которого прямые, является прямоугольником (№122).

2. Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине (№124).

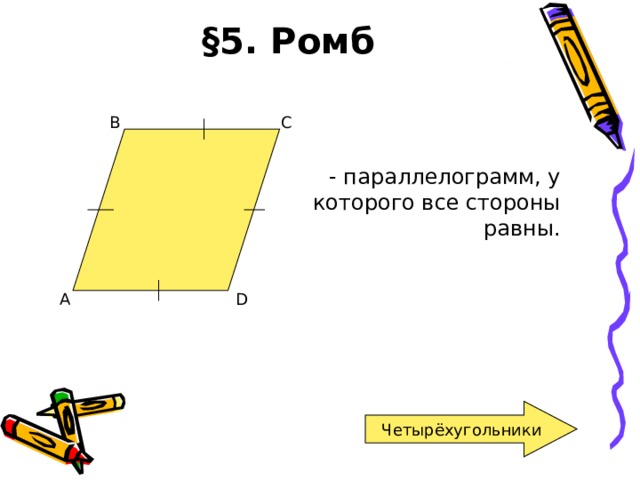
§ 5. Ромб

В

С

- параллелограмм, у которого все стороны равны.

А

D

Четырёхугольники

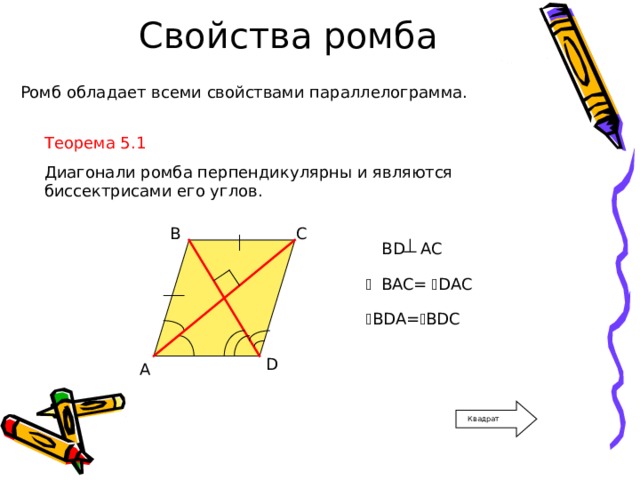
Свойства ромба

Ромб обладает всеми свойствами параллелограмма.

Теорема 5.1

Диагонали ромба перпендикулярны и являются биссектрисами его углов.

B

C

BD AC

 BAC=  DAC

 BDA=  BDC

D

A

Квадрат

Теорема 5 .2

Если диагонали параллелограмма перпендикулярны, то данный параллелограмм - ромб .

Теорема 5 .3

Если диагональ параллелограмма является биссектрисой его угла, то данный параллелограмм - ромб.

Ключевые задачи

1. Докажите, что если две соседние стороны параллелограмма равны, то этот параллелограмм является ромбом (№137).

2. Докажите, что четырехугольник, у которого все стороны равны, является ромбом (№138).

3. Докажите, что высоты ромба равны (№148).

Квадраты

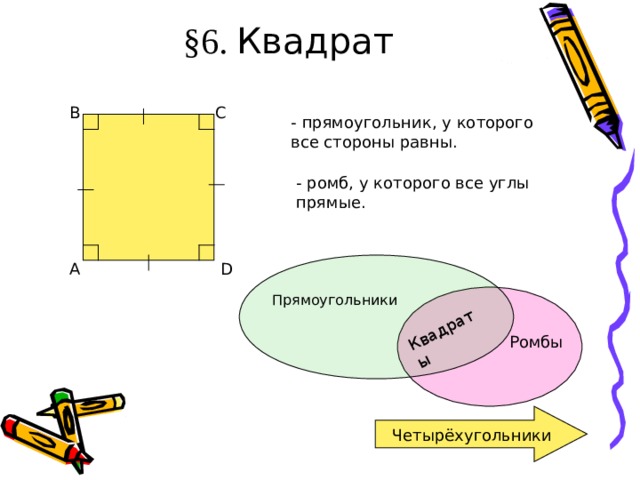
§ 6. Квадрат

B

C

- прямоугольник, у которого все стороны равны.

- ромб, у которого все углы прямые.

D

A

Прямоугольники

Ромбы

Четырёхугольники

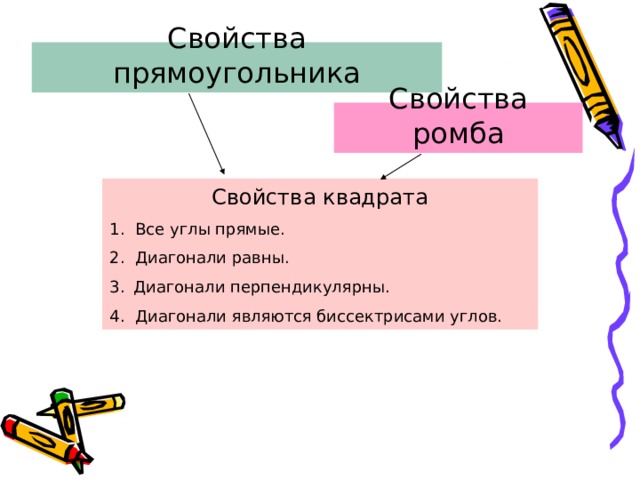
Свойства прямоугольника

Свойства ромба

Свойства квадрата

1. Все углы прямые.

2. Диагонали равны.

• Диагонали перпендикулярны.

4. Диагонали являются биссектрисами углов.

Ключевые задачи

1. Докажите, что если один из углов ромба прямой, то этот ромб является квадратом (№165).

2. Докажите, что если две соседние стороны прямоугольника равны, то этот прямоугольник является квадратом (№166).

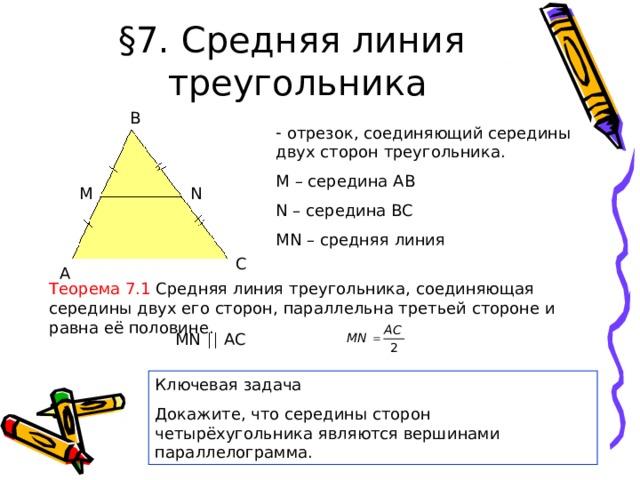
§ 7. Средняя линия

треугольника

В

• отрезок, соединяющий середины двух сторон треугольника.

M – середина АВ

N – середина ВС

MN – средняя линия

M

N

С

А

Теорема 7.1 Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.

MN  AC

Ключевая задача

Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма.

боковая сторона

боковая сторона

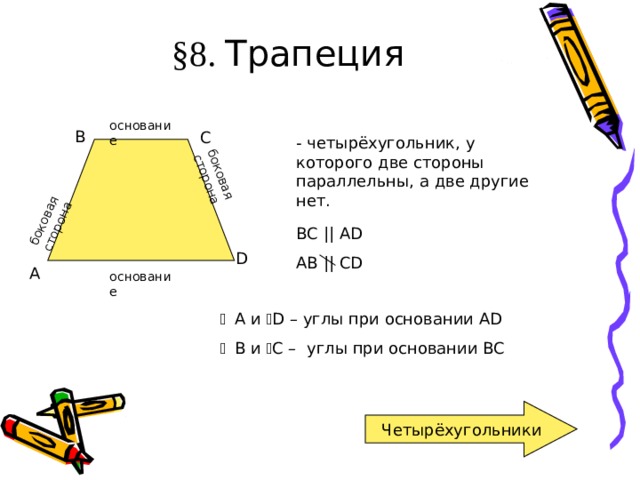
§ 8. Трапеция

B

основание

C

- четырёхугольник, у которого две стороны параллельны, а две другие нет.

ВС || AD

AB || CD

D

A

основание

 A и  D – углы при основании AD

 B и  C – углы при основании BC

Четырёхугольники

C

B

M

L

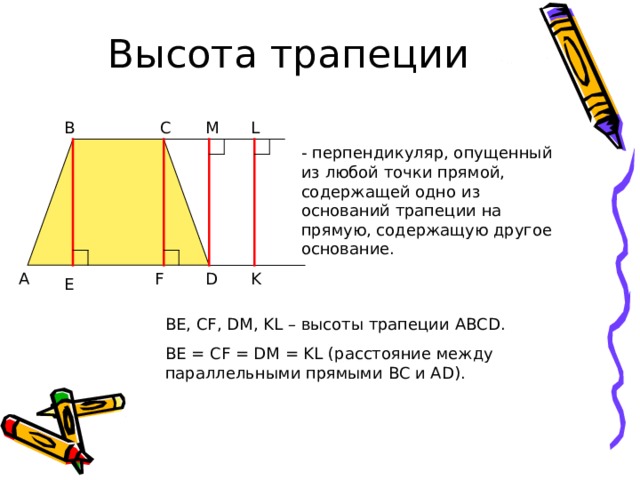
- перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований трапеции на прямую, содержащую другое основание.

А

D

F

K

E

BE, CF, DM, KL – высоты трапеции ABCD .

BE = CF = DM = KL ( расстояние между параллельными прямыми BC и AD) .

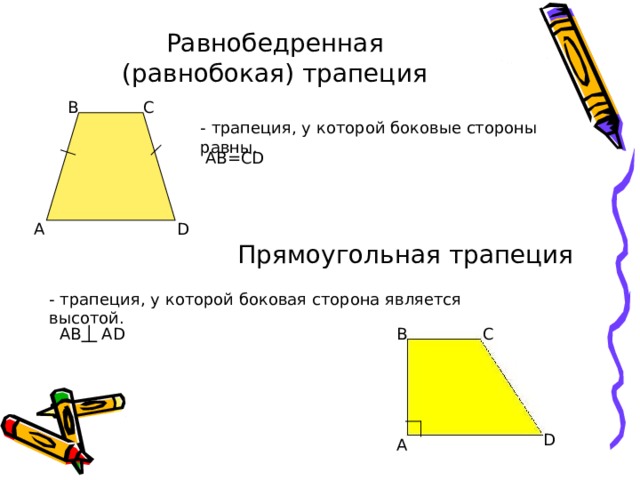
Равнобедренная (равнобокая) трапеция

C

B

- трапеция, у которой боковые стороны равны.

AB=CD

D

A

Прямоугольная трапеция

- трапеция, у которой боковая сторона является высотой.

С

AB AD

В

D

А

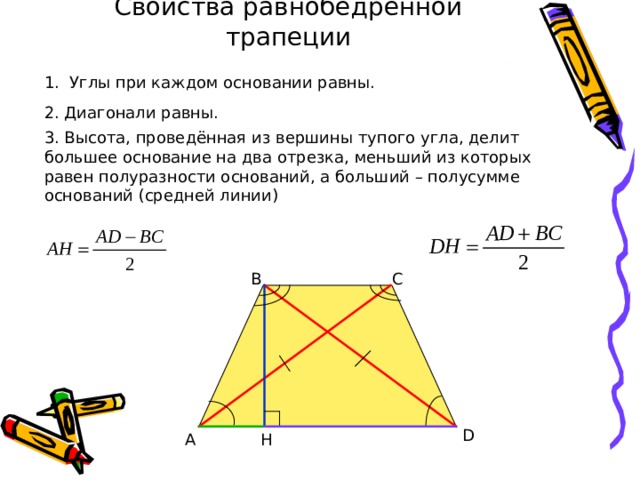
Свойства равнобедренной трапеции

1. Углы при каждом основании равны.

2. Диагонали равны.

3. Высота, проведённая из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований (средней линии)

C

B

D

A

H

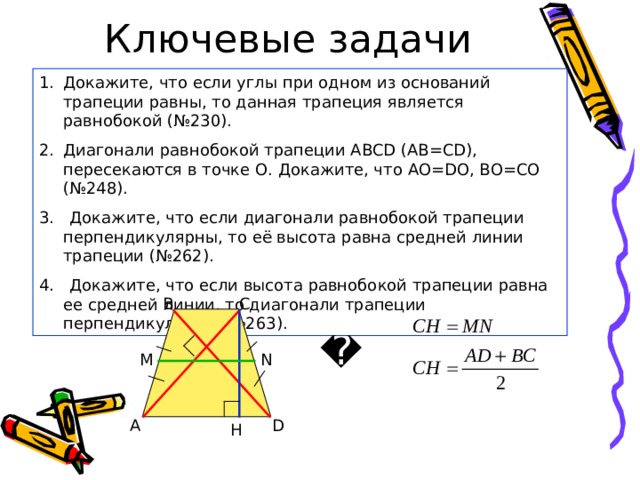
• Докажите, что если углы при одном из оснований трапеции равны, то данная трапеция является равнобокой (№230).

• Диагонали равнобокой трапеции ABCD ( AB=CD ), пересекаются в точке О. Докажите, что AO=DO, BO=CO ( №248) .

3. Докажите, что если диагонали равнобокой трапеции перпендикулярны, то её высота равна средней линии трапеции (№262).

4. Докажите, что если высота равнобокой трапеции равна ее средней линии, то диагонали трапеции перпендикулярны (№263).

B

C

M

N

D

A

Н

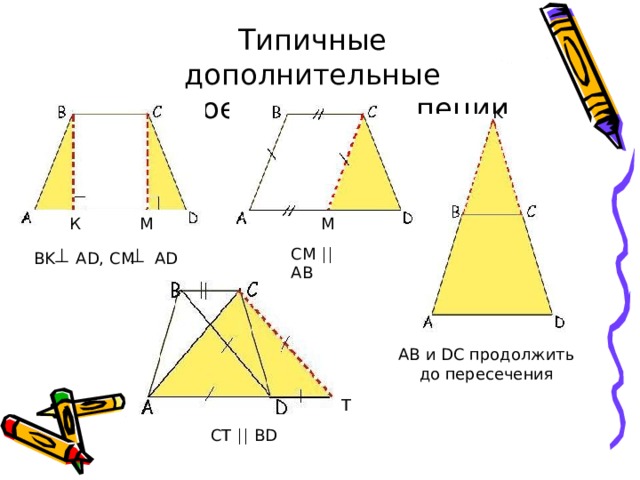
Типичные дополнительные построения для трапеции

K

К

М

M

CM  AB

BK AD, CM AD

AB и DC продолжить до пересечения

Т

CT  BD

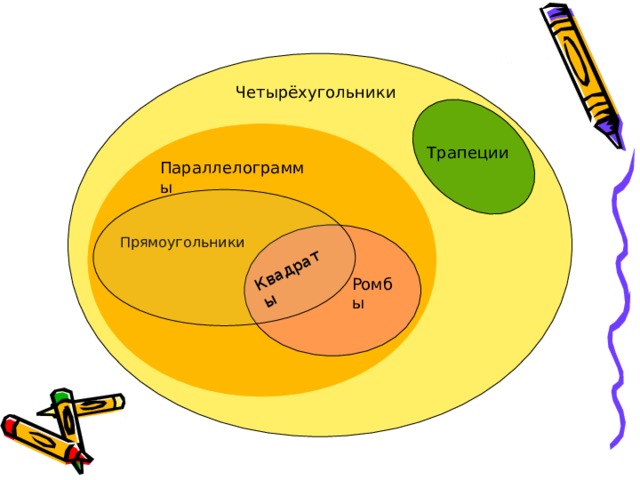
Квадраты

Четырёхугольники

Трапеции

Параллелограммы

Прямоугольники

Ромбы

Список использованных источников

• Мерзляк А.Г. Геометрия : 8 класс : учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В. Б. Полонский, М.С. Якир. – М. : Вентана-Граф, 2018. – 208 с.

• Нелин Е. Геометрия. 7-11 классы. Определения, свойства,

методы решения задач - в таблицах. /  Е. П. Нелин. - 2-е

изд., испр. - Москва : Илекса, 2019. - 80 с.