Россия, Джанкой
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.05.2025 10:30
Левченко Людмила Валентиновна
учитель математики и физики
57 лет
2 794
21 224 
Местоположение
Специализация
Презентация функции и их графики
Категория:
Математика
05.03.2019 19:12
Просмотр содержимого документа
«Презентация функции и их графики»
Функции и их свойства
y
y = f( x )
x
0
Понятие функции
Если каждому значению х из некоторого множества чисел поставлено в соответствие число у , то говорят, что на этом множ е стве задана функция у(х) .
При этом х называют независимой переменной или аргументом ,
а у – зависимой переменной или функцией .
y = f(x)
Область определения и
множество значений функции
Областью определения функции называют множество всех значений, которые может принимать ее аргумент.
Обозначается D(y)
Множество значений (или область значений) функции – это множество всех значений переменной у.
Обозначается E(y)
Способы задания функции:
- аналитический (с помощью формулы);
- графический (с помощью графика);
- табличный (с помощью таблицы значений);
- словесный (правило задания функции описывается словами).
f(x 2 ) . (Функцию называют убывающей, если большему значению аргумента соответствует меньшее значение функции) " width="640"
Свойства функций:
монотонность
Функцию y = f(x) называют возрастающей на множестве Х, если для любых двух элементов из этого множества, таких, что х 1 2 , выполняется условие f(x 1 ) 2 ) .
(Функцию называют возрастающей, если большему значению аргумента соответствует большее значение функции)
Функцию y = f(x) называют убывающей на множестве Х, если для любых двух элементов из этого множества, таких, что х 1 2 , выполняется условие f(x 1 ) f(x 2 ) .
(Функцию называют убывающей, если большему значению аргумента соответствует меньшее значение функции)
m . Функцию y = f(x) называют ограниченной сверху на множестве Х, если существует число M , такое, что для любого значения х ∊ Х, выполняется неравенство f(x) M . Если функция ограничена и снизу и сверху, то ее называют ограниченной " width="640"
Свойства функций:
ограниченность
Функцию y = f(x) называют ограниченной снизу на множестве Х, если существует число m , такое, что для любого значения х ∊ Х, выполняется неравенство
f(x) m .
Функцию y = f(x) называют ограниченной сверху на множестве Х, если существует число M , такое, что для любого значения х ∊ Х, выполняется неравенство
f(x) M .
Если функция ограничена и снизу и сверху, то ее называют ограниченной
Свойства функций:
наибольшее и наименьшее значения функции
Число m называют наименьшим значением функции y = f(x) на множестве Х, если:
существует число х о ∊ Х такое, что f( х o ) = m ;
для любого значения х ∊ Х выполняется неравенство
f(x) ≥ f(x o ) .
Число М называют наибольшим значением функции y = f(x) на множестве Х, если:
существует число х о ∊ Х такое, что f( х o ) = М ;
для любого значения х ∊ Х выполняется неравенство
f(x) ≤ f(x o ) .
Свойства функций:
четность или нечетность
Функцию y = f(x) , х ∊ Х называют четной , если для любого значения х из множества Х выполняется равенство f( - x) = f(x) .
График четной функции симметричен относительно оси ординат .
Функцию y = f(x) , х ∊ Х называют нечетной , если для любого значения х из множества Х выполняется равенство f( – x) = – f(x) .
График нечетной функции симметричен относительно начала координат .
f(x o ) . Точки максимума и минимума объединяют общим названием – точки экстремума " width="640"
Свойства функций:
точки экстремума
Точку х о называют точкой максимума функции y = f(x) , если у этой точки существует окрестность, для всех точек которой (кроме самой точки х о ) выполняется неравенство
f(x) f(x o ) .
Точку х о называют точкой минимума функции y = f(x) , если у этой точки существует окрестность, для всех точек которой (кроме самой точки х о ) выполняется неравенство
f(x) f(x o ) .
Точки максимума и минимума объединяют общим названием – точки экстремума
Свойства функций:
периодичность
Говорят, что функция y = f(x) , х ∊ Х имеет период Т , если для любого х ∊ Х выполняется равенство
f(x – Т ) = f(x) = f(x + T) .
Функцию, имеющую отличный от нуля период называют периодической .
Если функция y = f(x) , х ∊ Х имеет период Т, то любое число, кратное Т (т.е. число вида kT , k ∊ Z ), также является ее периодом.
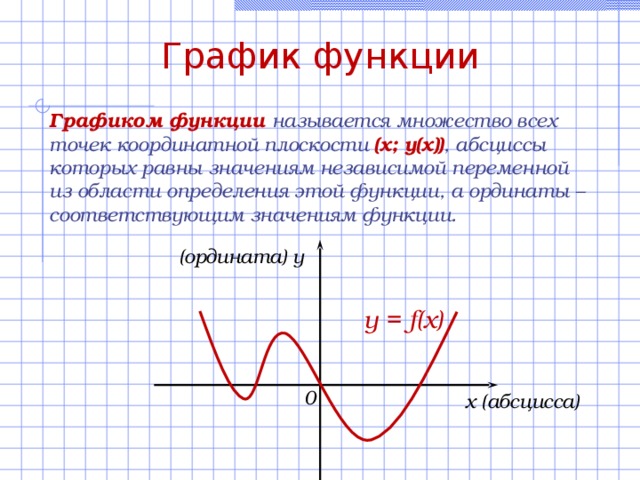
График функции
Графиком функции называется множество всех точек координатной плоскости (х; у(х)) , абсциссы которых равны значениям независимой переменной из области определения этой функции, а ординаты – соответствующим значениям функции.
(ордината) y
y = f( x )
0
x (абсцисса)
Основные элементарные
функции, их свойства
и графики
0 ; б) убывает , если k . Не ограничена ни снизу, ни сверху. Нет ни наибольшего, ни наименьшего значений. Функция непрерывна на множестве (– ; + ) . " width="640"
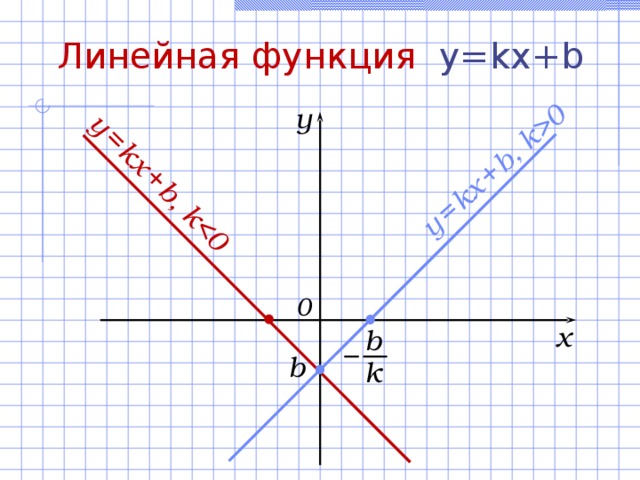
Линейная функция y=kx+b
Свойства линейной функции y = kx + b :
- D(f) = (– ; + ) .
- E(f) = (– ; + ) .
- Если b = 0 , то функция нечетная .
- а) Нули функции: ( – b/k; 0) ;
б) точка пересечения с Оу: (0; b) .
- а) возрастает , если k 0 ;
б) убывает , если k .
- Не ограничена ни снизу, ни сверху.
- Нет ни наибольшего, ни наименьшего значений.
- Функция непрерывна на множестве (– ; + ) .
0 y = kx + b , k Линейная функция y=kx+b y 0 x b b k " width="640"
y = kx + b , k0
y = kx + b , k
Линейная функция y=kx+b
y
0
x
b
b
k
0 , то (– ; 0) и (0; + ) – промежутки убывания функции. Не ограничена ни снизу, ни сверху. Нет ни наибольшего, ни наименьшего значений. Функция непрерывна на каждом из промежутков (– ; 0) и (0; + ) . " width="640"
k
у =
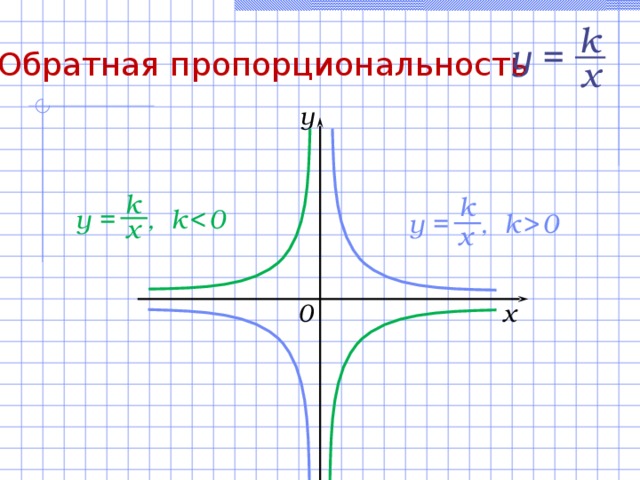
Обратная пропорциональность
x
Свойства функции y = k/x :
- D(f) = (– ; 0) (0; + ) .
- E(f) = (– ; 0) (0; + ) .
- Функция нечетная.
- а) Нули функции: нет ;
б) точка пересечения с Оу: нет .
- а) если k , то (– ; 0) и (0; + ) – промежутки возрастания функции ;
б) если k 0 , то (– ; 0) и (0; + ) – промежутки убывания функции.
- Не ограничена ни снизу, ни сверху.
- Нет ни наибольшего, ни наименьшего значений.
- Функция непрерывна на каждом из промежутков
(– ; 0) и (0; + ) .
0 x x x 0 " width="640"
k
у =
Обратная пропорциональность
x
y
k
k
у = , k 0
у = , k 0
x
x
x
0
0 : D(f) = (– ; + ) . E(f) = [0; + ) . Функция четная . а) Нули функции: (0; 0) ; б) точка пересечения с Оу: (0; 0) . а) [0; + ) – промежуток возрастания функции ; б) (– ; 0] – промежуток убывания функции. Ограничена снизу, не ограничена сверху. а) у наим. = 0; б) у наиб. – не существует. Непрерывна на множестве (– ; + ) . Выпукла вниз. " width="640"
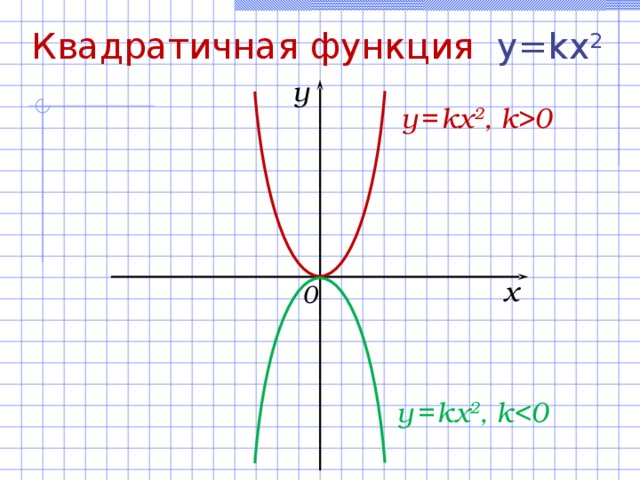
Квадратичная функция y= k x 2
Свойства функции y = kx 2 при k 0 :
- D(f) = (– ; + ) .
- E(f) = [0; + ) .
- Функция четная .
- а) Нули функции: (0; 0) ;
б) точка пересечения с Оу: (0; 0) .
- а) [0; + ) – промежуток возрастания функции ;
б) (– ; 0] – промежуток убывания функции.
- Ограничена снизу, не ограничена сверху.
- а) у наим. = 0;
б) у наиб. – не существует.
- Непрерывна на множестве (– ; + ) .
- Выпукла вниз.
![Квадратичная функция y= k x 2 Свойства функции y = kx 2 при k : D(f) = (– ; + ) . E(f) = (– ; 0] . Функция четная . а) Нули функции: (0; 0) ; б) точка пересечения с Оу: (0; 0) . а) [0; + ) – промежуток убывания функции ; б) (– ; 0] – промежуток возрастания функции. Ограничена сверху, не ограничена снизу. а) у наиб. = 0; б) у наим. – не существует. Непрерывна на множестве (– ; + ) . Выпукла вверх.](https://fsd.multiurok.ru/html/2019/03/05/s_5c7e9f5f83ab7/img17.jpg)
Квадратичная функция y= k x 2
Свойства функции y = kx 2 при k :
- D(f) = (– ; + ) .
- E(f) = (– ; 0] .
- Функция четная .
- а) Нули функции: (0; 0) ;
б) точка пересечения с Оу: (0; 0) .
- а) [0; + ) – промежуток убывания функции ;
б) (– ; 0] – промежуток возрастания функции.
- Ограничена сверху, не ограничена снизу.
- а) у наиб. = 0;
б) у наим. – не существует.
- Непрерывна на множестве (– ; + ) .
- Выпукла вверх.
0 x 0 y = kx 2 , k " width="640"
Квадратичная функция y= k x 2
y
y = kx 2 , k0
x
0
y = kx 2 , k
Степенная функция y= x
Свойства функции y = x :
- D(f) = [0; + ) .
- E(f) = [0; + ) .
- Функция ни четная , ни нечетная .
- а) Нули функции: (0; 0) ;
б) точка пересечения с Оу: (0; 0) .
- [0; + ) – промежуток возрастания функции.
- Ограничена снизу, не ограничена сверху.
- а) у наим. = 0;
б) у наиб. – не существует.
- Непрерывна на множестве [0; + ) .
- Выпукла вверх.
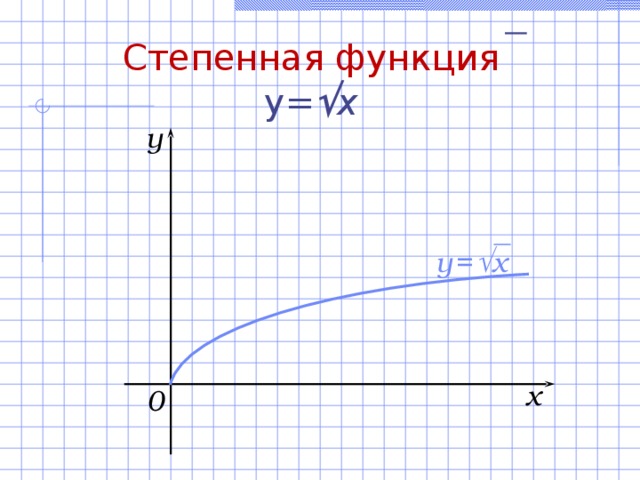
Степенная функция y= x
y
y = x
x
0
Кубическая функция y=x 3
Свойства кубической функции y = x 3 :
- D(f) = (– ; + ) .
- E(f) = (– ; + ) .
- Функция нечетная .
- а) Нули функции: ( 0 ; 0) ;
б) точка пересечения с Оу: (0; 0 ) .
- Возрастает на множестве (– ; + ) .
- Не ограничена ни снизу, ни сверху.
- Нет ни наибольшего, ни наименьшего значений.
- Функция непрерывна на множестве (– ; + ) .
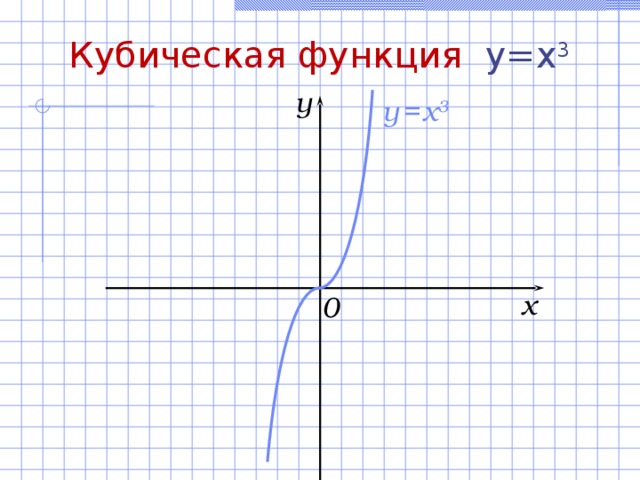
Кубическая функция y=x 3
y
y = x 3
x
0
п
Степенная функция y= x , х ≥ 0
n
Свойства функции y = x , х ≥ 0 :
- D(f) = [0; + ) .
- E(f) = [0; + ) .
- Функция ни четная , ни нечетная .
- а) Нули функции: (0; 0) ;
б) точка пересечения с Оу: (0; 0) .
- [0; + ) – промежуток возрастания функции.
- Ограничена снизу, не ограничена сверху.
- а) у наим. = 0;
б) у наиб. – не существует.
- Непрерывна на множестве [0; + ) .
- Выпукла вверх.
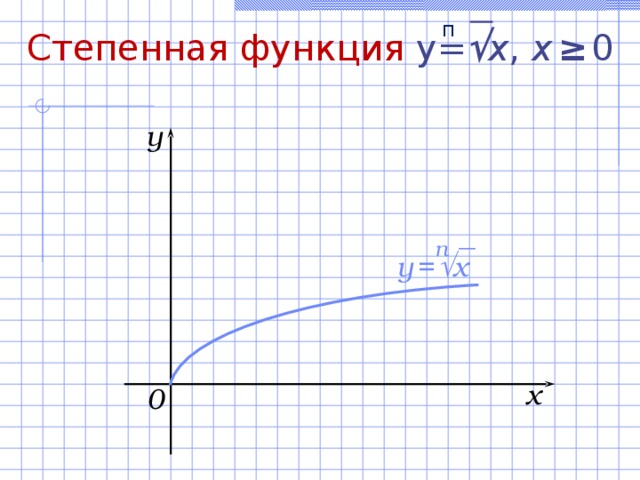
п
Степенная функция y= x , х ≥ 0
y
п
y = x
x
0
п
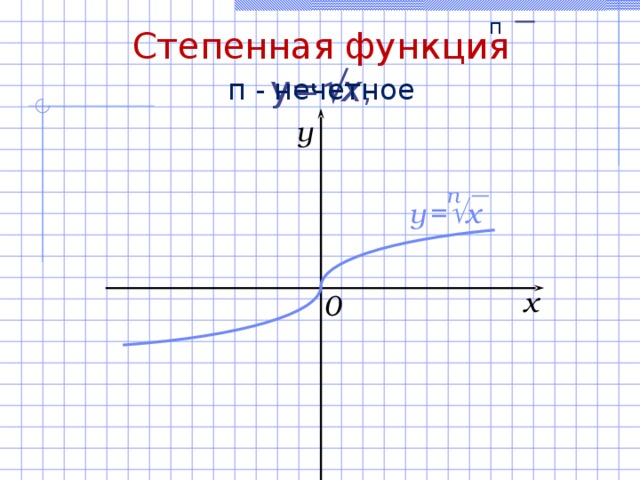
Степенная функция y= x ,
п - нечетное
n
Свойства функции y = x , n = 2k+1 :
- D(f) = (– ; + ) .
- E(f) = (– ; + ) .
- Функция нечетная .
- а) Нули функции: ( 0 ; 0) ;
б) точка пересечения с Оу: (0; 0 ) .
- Возрастает на множестве (– ; + ) .
- Не ограничена ни снизу, ни сверху.
- Нет ни наибольшего, ни наименьшего значений.
- Функция непрерывна на множестве (– ; + ) .
п
Степенная функция y= x ,
п - нечетное
y
п
y = x
x
0
© 2019, Левченко Людмила Валентиновна 2047 83
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
