Презентация к уроку алгебры "Функции. График функции"

Функция . График функции .

Линейные уравнения

• Задание: являются ли числа –1, 0, 2 корнями уравнения:

4х-8=х-2

• Найдите корень уравнения

– 0,3х = 6 1) 0,5; 2) -2; 3) – 20;

• Решите уравнение

а) 2х+3=0 1)1,5; 2) -2/3; 3) – 1,5;

б) 0,5(8х – 3) = -3(2,5 – х)

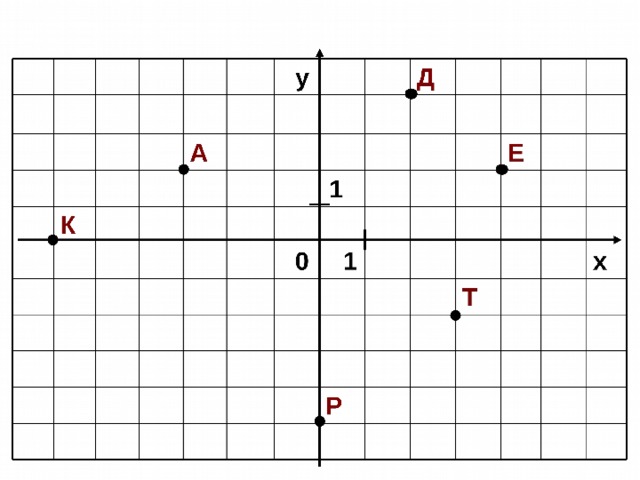
Теоретическая разминка

• Что такое функция?
• Приведите примеры функции.
• Что такое аргумент функции?
• Что такое область определения функции?
• Что такое область значения функции?
• Как можно задавать функции?
• Что такое график функции?

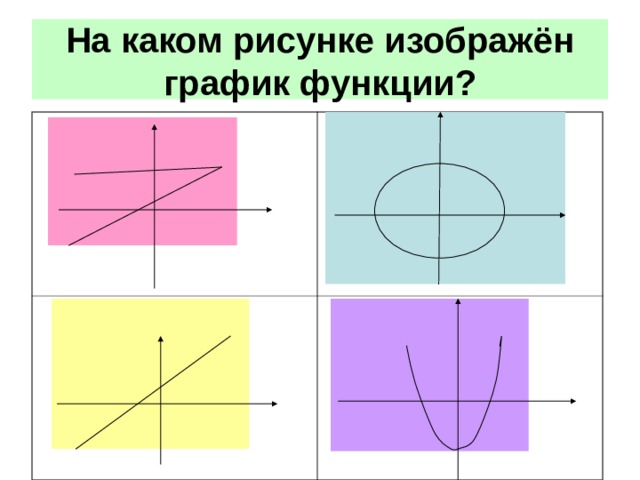
На каком рисунке изображён график функции?

Историческая пауза

Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции явно и вполне сознательно применяется.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.

Кроме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей “Геометрии” в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы.

Рене Декарт

Задание функции с помощью формулы

Формула позволяет для любого значения

аргумента находить соответствующее

значение функции путём вычислений.

Пример 1.

Найти значение функции y = x 3 + x

при х = - 2; х = 5; х = а; .

у = (-2) 3 + (-2) = -8 – 2 = -10

1.

у =

2.

у =

3.

Задание функции с помощью формулы

Формула позволяет для любого значения

аргумента находить соответствующее

значение функции путём вычислений.

Пример 1.

Найти значение функции y(x) = x 3 + x

при х = - 2; х = 5; х = а; х = 3а .

у = (-2) 3 + (-2) = -8 – 2 = -10

1.

у = 5 3 + 5 = 125 + 5 = 130

2.

у = а 3 + а

3.

у = (3 а ) 3 + 3 а = 27 а 3 + 3 а

4.

Машина движется по шоссе с постоянной скоростью

70 км/ч. За время t ч машина проходит путь

S = 70 · t км .

Легко вычислить пройденный путь за любое время:

Если t = 0,5 ,то

S =

S =

Если t = 1,5, то

S =

Если t = 2/7, то

S = 70 · t

Переменная - ?

Переменная -?

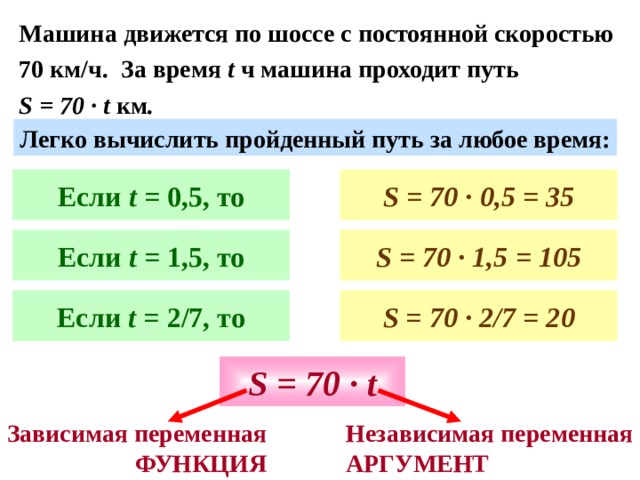
Машина движется по шоссе с постоянной скоростью

70 км/ч. За время t ч машина проходит путь

S = 70 · t км .

Легко вычислить пройденный путь за любое время:

Если t = 0,5, то

S = 70 · 0,5 = 35

Если t = 1,5, то

S = 70 · 1,5 = 105

Если t = 2/7, то

S = 70 · 2/7 = 2 0

S = 70 · t

Независимая переменная

АРГУМЕНТ

Зависимая переменная

ФУНКЦИЯ

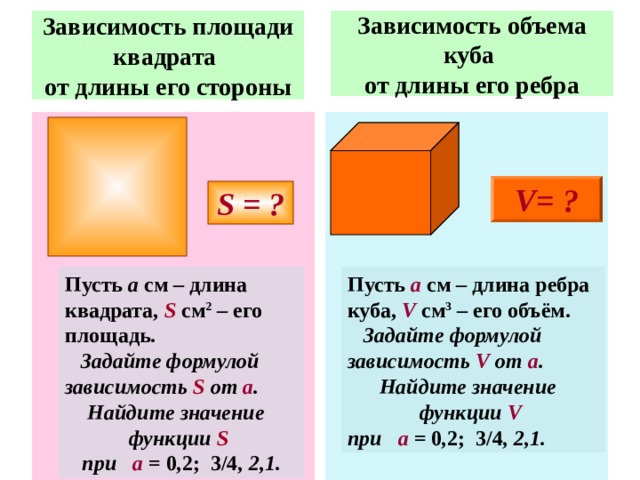
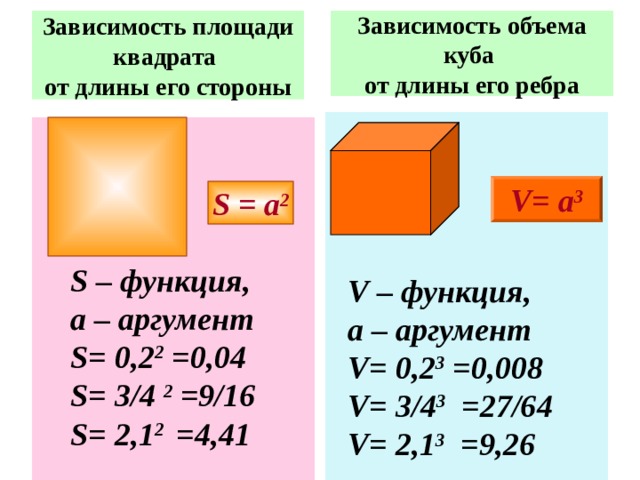
Зависимость площади квадрата от длины его стороны

Зависимость объема куба от длины его ребра

V= ?

S = ?

Пусть а см – длина ребра куба, V см 3 – его объём.

Задайте формулой зависимость V от а .

Найдите значение функции V

при а = 0 , 2; 3/4 , 2,1.

Пусть а см – длина квадрата, S см 2 – его площадь.

Задайте формулой зависимость S от а .

Найдите значение функции S

при а = 0 , 2; 3/4 , 2,1.

Зависимость площади квадрата от длины его стороны

Зависимость объема куба от длины его ребра

V= а 3

S = а 2

S – функция,

а – аргумент

S= 0 , 2 2 =0,04

S= 3/4 2 =9/16

S = 2,1 2 =4,41

V – функция,

а – аргумент

V= 0 , 2 3 =0,0 08

V= 3/4 3 = 27 /6 4

V = 2,1 3 = 9 , 26

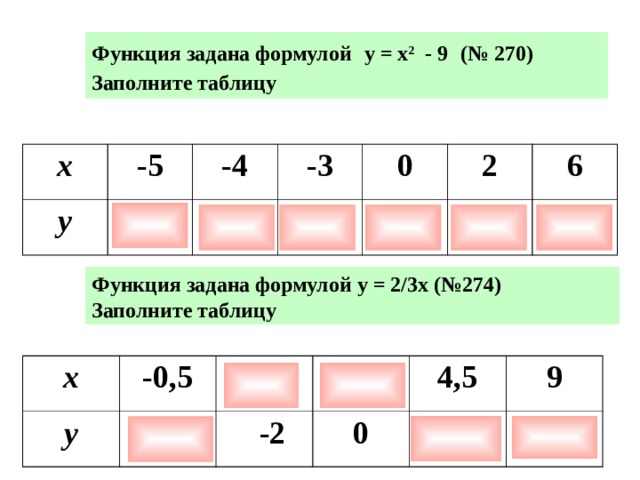
Функция задана формулой у = х 2 - 9 (№ 270)

Заполните таблицу

x

- 5

y

- 4

-3

0

2

6

Функция задана формулой у = 2/3х (№274)

Заполните таблицу

x

y

- 0,5

-2

4,5

0

9

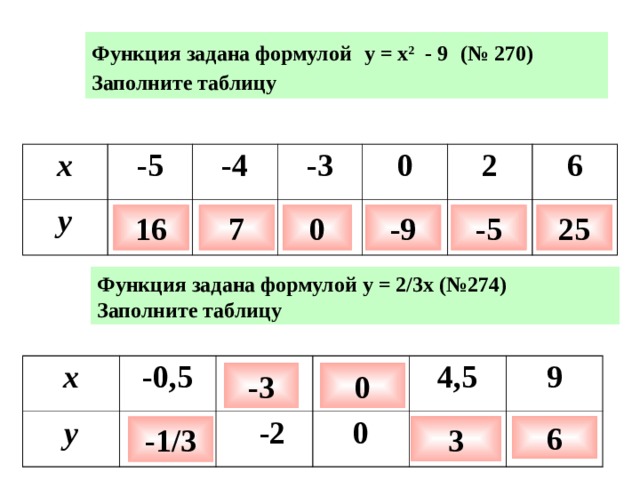
Функция задана формулой у = х 2 - 9 (№ 270)

Заполните таблицу

x

- 5

y

- 4

-3

0

2

6

-9

-5

25

0

7

16

Функция задана формулой у = 2/3х (№274)

Заполните таблицу

x

y

- 0,5

-2

4,5

0

9

0

-3

3

6

-1/3

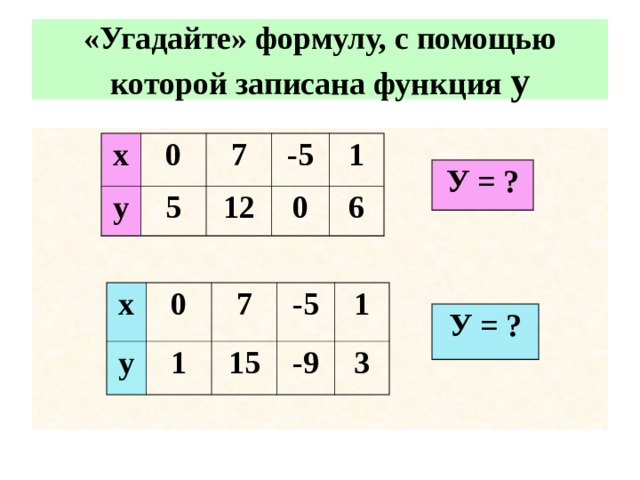
«Угадайте» формулу, с помощью которой записана функция у

х

0

у

7

5

-5

12

1

0

6

У = ?

х

у

0

7

1

-5

15

1

-9

3

У = ?

№ 273, стр. 57; № 276, стр. 57

Задайте формулой зависимость массы куска пробки от его объема, если известно, что плотность пробки равна 0, 18 г/см 3 . Найдите по формуле:

а) массу куска пробки, объем которого равен 240 см 3;

б)объем куска пробки, масса которого равна 64,8 г.

Формула у= -5х+6 задаёт некоторую функцию. При каком значении аргумента значение функции равно 6? 8?

№ 273, стр. 57; № 276, стр. 57

m = v * р :

а) m =240*0,18

m =43,2

б) 64,8= V *0,18

V =6 4 , 8 :0,18

V = 360

• х=6

-5х+6=6, -5х=6-6

- 5х=0, х=0

• х=8

-5х+6=8, - 5х=8-6,

-5х=2, х=-0,4

«В гостях у медиков»

Медики установили, что для нормального развития ребенок, младше 18 лет должен спать в сутки t часов,

t = 17 – T /2 , где T - возраст ребенка, T

• - Если считать что вам 13 лет. Сколько часов в сутки вы должны спать?

- А сколь лет школьнику, который спит 10 часов в сутки?

• Скажите, как называется зависимость между

t и T ?

«Сказочный мир»

Во дворце подводного царства очень много ( у) зеркал. В первом зале дворца в 4 раза больше, чем во втором (х), а в третьем на 40 зеркал больше, чем во втором. Задайте функцию формулой. Сколько зеркал в каждом зале, если у=280?

«Сказочный мир»

у = х+4х+(х+40)

280 = х+4х+(х+40)

х+4х+х+40 = 280

6х = 280, х=40

Ответ:

В первом – 160

Во втором - 40

В третьем – 80

Метеорология

Медицина

Сейсмология

Графики

вокруг

нас

Математика,

физика

Статистика

Экономика

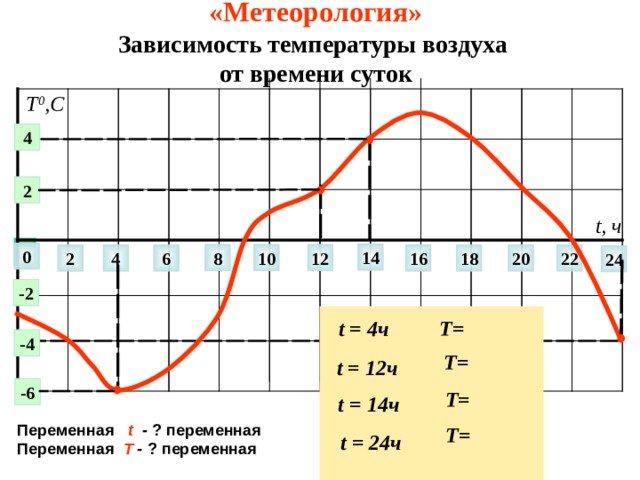
«Метеорология» Зависимость температуры воздуха от времени суток

Т 0 ,С

4

2

t , ч

0

14

8

10

12

20

18

16

22

6

4

2

24

-2

Т=

t = 4ч

-4

Т=

t = 12ч

-6

Т=

t = 14ч

Переменная t - ? переменная

Переменная T - ? переменная

Т=

t = 24ч

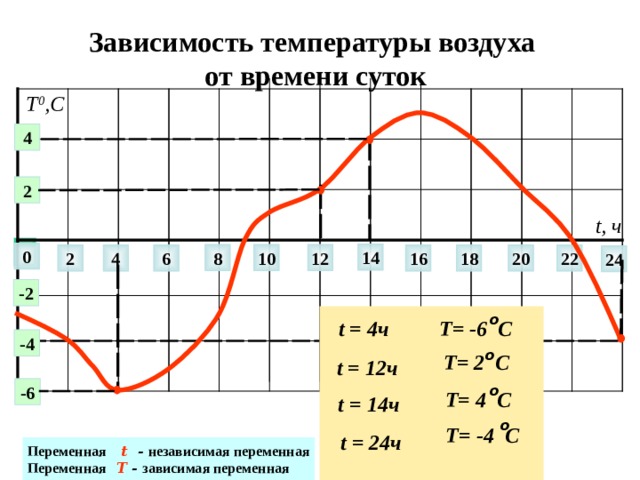
Зависимость температуры воздуха от времени суток

Т 0 ,С

4

2

t , ч

0

14

8

10

12

20

18

16

22

6

4

2

24

-2

о

Т= -6 С

t = 4ч

-4

о

Т= 2 С

t = 12ч

о

-6

Т= 4 С

t = 14ч

о

Т= -4 С

t = 24ч

Переменная t - независимая переменная

Переменная T - зависимая переменная

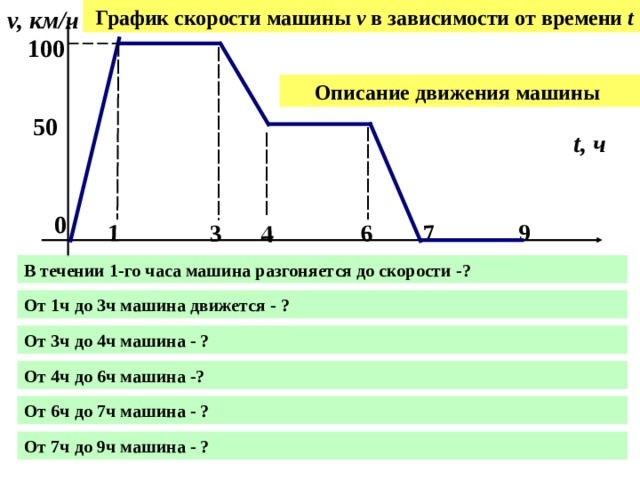
График скорости машины v в зависимости от времени t

v, км/ч

1

3

4

6

7

9

100

Описание движения машины

5 0

t, ч

0

В течении 1-го часа машина разгоняется до скорости -?

От 1ч до 3ч машина движется - ?

От 3ч до 4ч машина - ?

От 4ч до 6ч машина -?

От 6ч до 7ч машина - ?

От 7ч до 9ч машина - ?

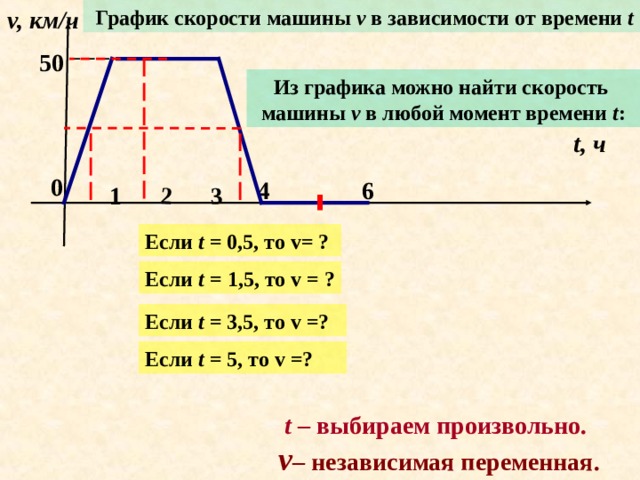
График скорости машины v в зависимости от времени t

v, км/ч

1

3

6

2

5 0

Из графика можно найти скорость

машины v в любой момент времени t :

t, ч

4

0

Если t = 0,5, то v= ?

Если t = 1,5, то v = ?

Если t = 3,5, то v =?

B Используется триггер. При нажатии на жёлтый прямоугольник – ответ на вопрос, какова скорость. При нажатии на розовый прямоугольник – проверка правильности ответа по графику

Если t = 5, то v =?

t – выбираем произвольно.

v – независимая переменная.

24

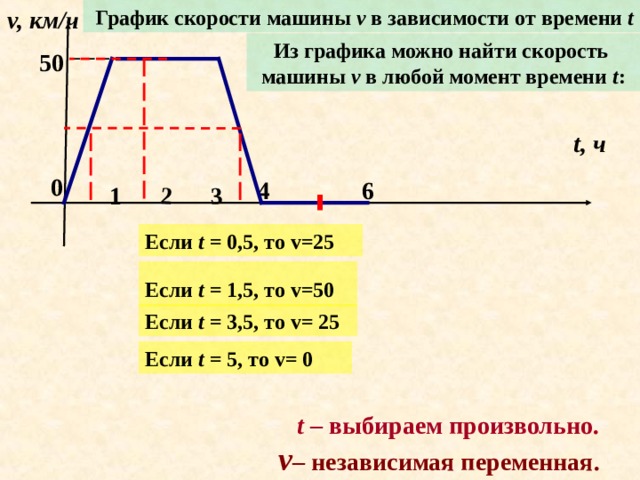
v, км/ч

График скорости машины v в зависимости от времени t

1

3

6

2

Из графика можно найти скорость

машины v в любой момент времени t :

5 0

t, ч

4

0

Если t = 0,5, то v=25

Если t = 1,5, то v=50

Если t = 3,5, то v= 25

B Используется триггер. При нажатии на жёлтый прямоугольник – ответ на вопрос, какова скорость. При нажатии на розовый прямоугольник – проверка правильности ответа по графику

Если t = 5, то v= 0

t – выбираем произвольно.

v – независимая переменная.

24

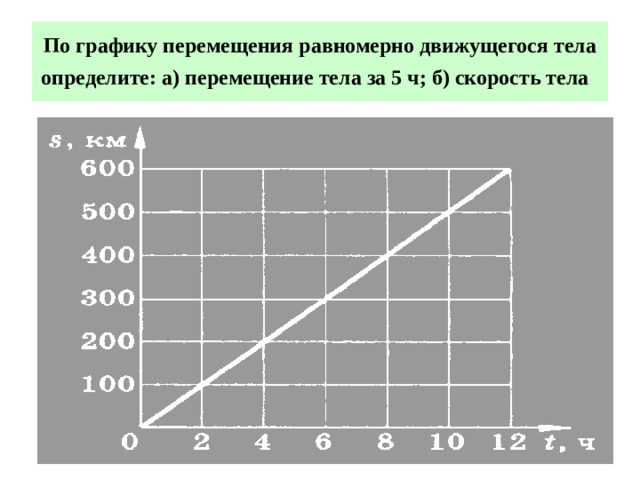
По графику перемещения равномерно движущегося тела определите: а) перемещение тела за 5 ч; б) скорость тела

Медицина. Кардиограмма работы сердца

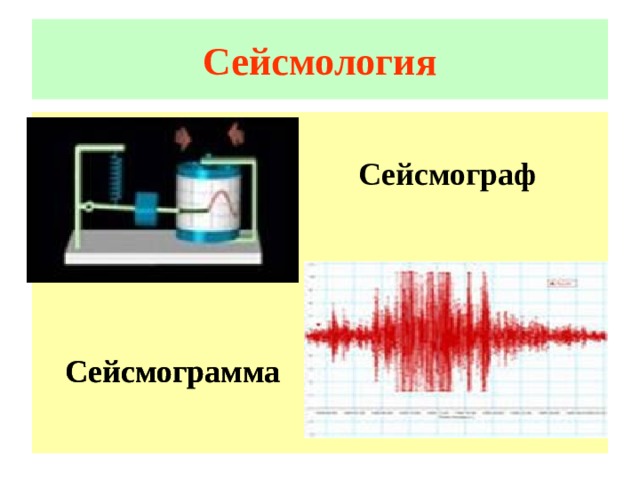
Сейсмология

Сейсмограф

Сейсмограмма

Сейсмограмма

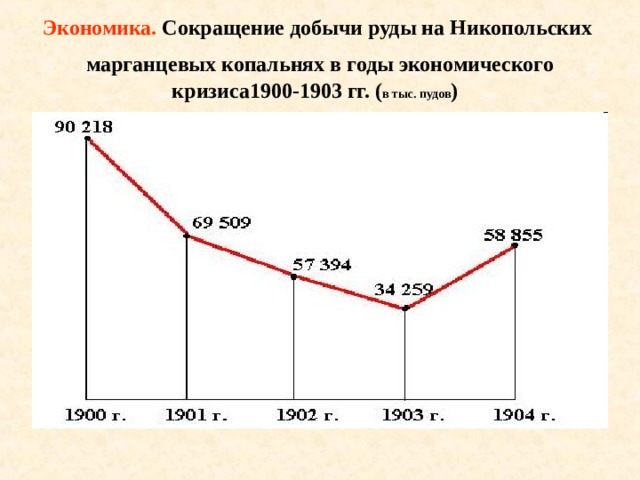
Экономика. Сокращение добычи руды на Никопольских марганцевых копальнях в годы экономического кризиса1900-1903 гг. ( в тыс. пудов )

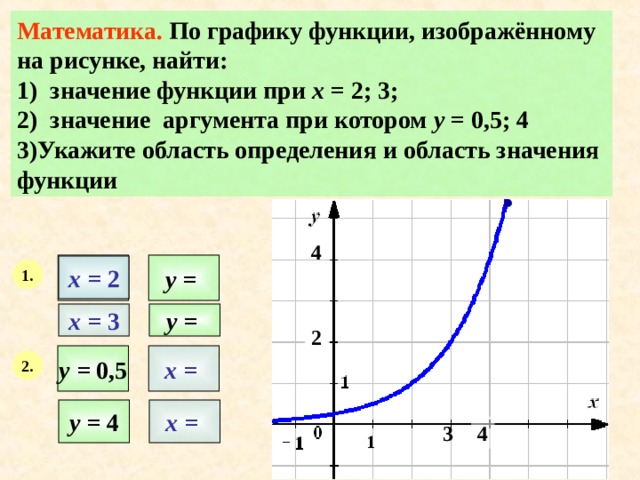
Математика. По графику функции, изображённому на рисунке, найти:

1) значение функции при х = 2; 3;

2) значение аргумента при котором у = 0,5; 4

3)Укажите область определения и область значения функции

.

4

х = 2

у =

х = 2

1.

х = 3

у =

2

х =

у = 0,5

2.

у = 4

х =

3

4

.

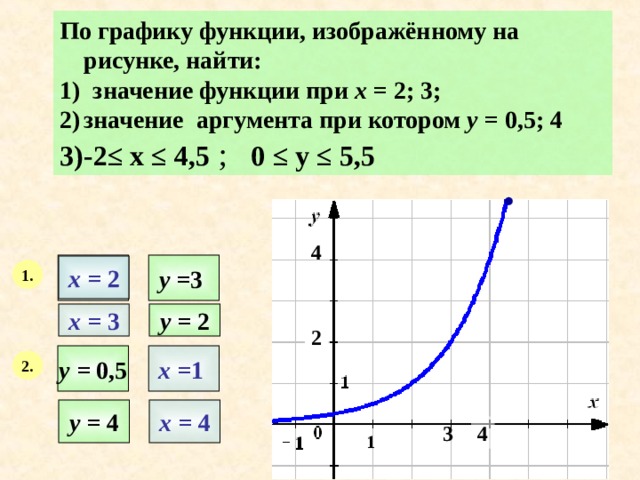
По графику функции, изображённому на рисунке, найти:

1) значение функции при х = 2; 3;

• значение аргумента при котором у = 0,5; 4
• -2≤ х ≤ 4,5 ; 0 ≤ у ≤ 5,5

4

х = 2

у = 3

х = 2

1.

у = 2

х = 3

2

у = 0,5

х = 1

2.

у = 4

х = 4

4

3

В рассмотренных примерах

каждому значению независимой

переменной соответствует

единственное значение

зависимой переменной.

Зависимость одной переменной

от другой называют

функциональной зависимостью

или функцией.

3. №287

Самостоятельная работа

• Найдите значение функции у = 3x + 1

1. Мама купила несколько конфет ( d ) по 5 рублей за конфету и одну шоколадку за 65 рублей. Сколько она заплатила за всю покупку ( n )? Найдите значение n , если d = 6

при х = - 1 .

а) 2, б) 4 , в) – 2 .

2. Функция задана формулой

у = - 2х + 3.

Найдите х, если у = 0.

а) х = 2/3, б) – 3/2, в) 3/2

3. № 285

а) 70 , б) 95 , в) 76 .

2. Функция задана

формулой у = - х/2 + 3. Заполнить

х

у

1

-3

0,5

-1

Итоги урока. Д/з.

• Итоги урока.

• Чему научились?
• Что показалось особенно трудным?
• Что понравилось?

• Д/з.

творческое задание : составить кроссворд по теме «Функция» (5-10 слов)