Презентация "Геометрические преобразования в пространстве"

Геометрические преобразования в пространстве

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• 1. Сколько плоскостей можно провести через три точки?
• 2. Сколько ребер у куба?
• 3. Сколько плоскостей можно провести через прямую и плоскость, не лежащую на данной прямой?
• 4. Сколько прямых, перпендикулярных к основанию куба?
• 5. Какими являются между собой два перпендикуляра к плоскости?
• 6. Как называются прямые, непараллельные и не пересекаются?
• 7. Сколько плоскостей можно провести через прямую?
• 8. Сколько плоскостей проходит через две пересекающиеся прямые?
• 9. Сколько вершин у куба?
• 10. Сколько параллельных пар плоскостей пар у куба?
• 11Как называются две плоскости, которые пересекаются под углом 90 градусов?
• 12. сколько плоскостей можно провести через точку?
• 13. Сколько плоских углов у куба?
• 14. Начертите куб. Обозначьте его.
• 15. Запишите примеры: параллельные прямые в кубе, скрещивающиеся прямые, параллельные плоскости, перпендикулярные плоскости.

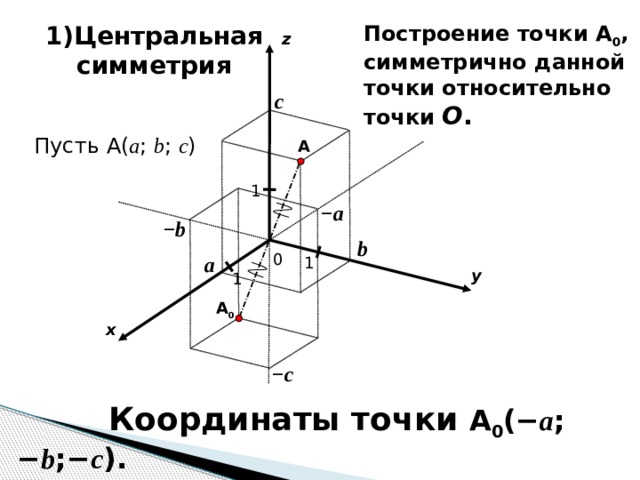
Построение точки A 0 , симметрично данной точки относительно точки O .

1)Центральная симметрия

z

c

Пусть A ( a ; b ; c )

A

1

− a

− b

b

0

a

1

y

1

A 0

x

− c

Координаты точки A 0 ( − a ; − b ;− c ).

2)Осевая симметрия

z

Построение точки A 1 , симметрично данной точки относительно оси Ox .

c

Пусть A ( a ; b ; c )

A

1

− b

b

0

a

1

y

1

x

− c

A 1

Координаты точки A 1 ( a ; − b ; − c ).

Осевая симметрия

z

Построим точку A 2 , симметричную данной точке относительно оси Oy .

c

Пусть A ( a ; b ; c )

A

1

− a

b

0

a

1

y

1

x

− c

A 2

Координаты точки A 2 (− a ; b ; − c ).

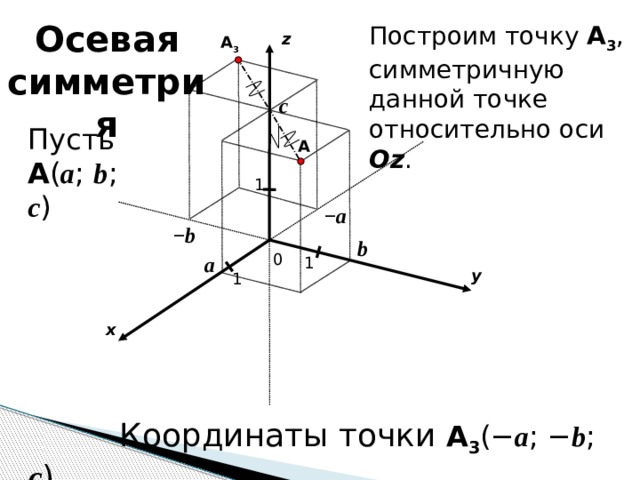
Осевая симметрия

Построим точку A 3 , симметричную данной точке относительно оси Oz .

z

A 3

c

Пусть A ( a ; b ; c )

A

1

− a

− b

b

0

a

1

y

1

x

Координаты точки A 3 (− a ; − b ; c ).

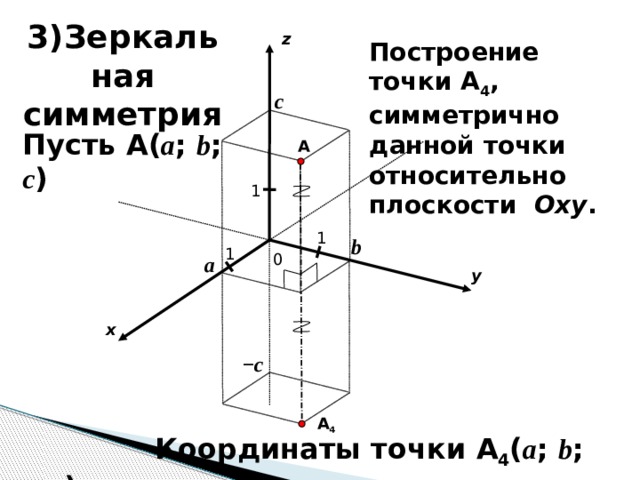
3)Зеркальная симметрия

z

Построение точки A 4 , симметрично данной точки относительно плоскости Oxy .

c

Пусть A ( a ; b ; c )

A

1

1

b

1

0

a

y

x

− c

A 4

Координаты точки A 4 ( a ; b ; − c ).

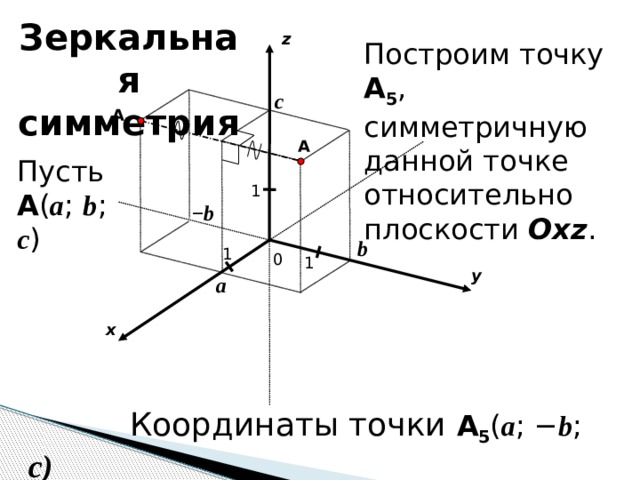
Зеркальная симметрия

z

Построим точку A 5 , симметричную данной точке относительно плоскости Oxz .

c

A 5

A

Пусть A ( a ; b ; c )

1

− b

b

1

0

1

y

a

x

Координаты точки A 5 ( a ; − b ; c)

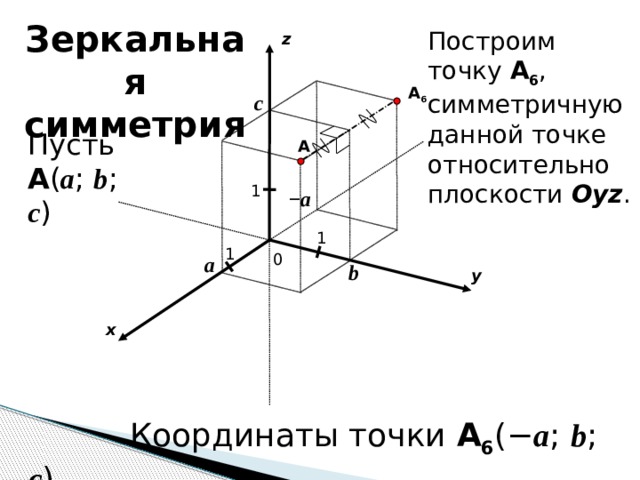
Зеркальная симметрия

Построим точку A 6 , симметричную данной точке относительно плоскости Oyz .

z

A 6

c

Пусть A ( a ; b ; c )

A

1

− a

1

1

0

a

b

y

x

Координаты точки A 6 (− a ; b ; c ).

Отражение в воде – хороший пример зеркальной симметрии играет ро о Отражение в воде – хороший пример зеркальной симметрии в природе.

Мы любуемся пейзажами художников, удачными снимками. Горы красиво отражаются на поверхности озера, придавая снимку законченность. Поверхность озера играет роль зеркала, и воспроизводит отражение с геометрической точностью. Поверхность воды есть плоскость симметрии...

с геометрической точностью. Поверхность

снимку законченность. Поверхность озера

Примерами зеркальных отражений одна другой могут служить рука человека .

4) Движение в пространстве

• Движением называется преобразование, при котором сохраняются расстояния между точками.

Основные свойства движения в пространстве

• Прямые переходят в прямые
• Полупрямые переходят в полупрямые
• Отрезки переходят в отрезки
• Сохраняются углы между полупрямыми
• Движение переводит плоскости в плоскости ( новое свойство )

Две фигуры называются равными , если они совмещаются движением

5) Параллельный перенос

Параллельный перенос в пространстве

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка ( x; y; z ) фигуры переходит в точку ( x + a; y + b; z + c ), где числа a, b, с одни и те же для всех точек ( x; y; z ). 

Параллельный перенос в пространстве обладает следующими свойствами :

1. Параллельный перенос есть движение. 

2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние. 

3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя. 

4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'. 

5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

6)Подобие пространственных фигур

Определение

• Преобразование фигуры F называется преобразованием подобия , Если при этом преобразовании расстояние между точками изменяется в одно и то же число раз .
• т. е. для любых двух точек X и У фигуры F и точек X', У фигуры F', в которые они переходят, X'Y' = k * XY.
• Две фигуры называются подобными , если они переводятся одна в другую преобразованием подобия.

Простейшим преобразованием подобия в пространстве является

Спасибо за урок!