Презентация «Готовимся к ОГЭ по информатике. Задание 8»

ОГЭ по информатике

Часть 1. Задание 8

Справочная информация

Для поиска информации существуют специальные поисковые службы, называемые поисковые серверы . Наиболее известные из них – yandex.ru, google.ru и другие.

Текст, который пользователь печатает в поле поиска, называется поисковым запросом .

Поисковая система анализирует слова в поисковом запросе, выделяет из них важные (ключевые) слова и по ним уже осуществляет поиск в собственных хранилищах. Ссылки на найденные страницы выдаются в качестве результата поискового запроса.

Чтобы поиск был более продуктивным, поисковые серверы позволяют указывать ключевые слова с использованием различных логических операций.

• логическое ИЛИ (дизъюнкция) , обозначаемая в поисковых запросах символом «|»;
• логическое И (конъюнкция) , обозначаемая в поисковых запросах символом «&».

Рассмотрим поисковый запрос на примере двух ключевых слов – «красный» и «синий».

Запрос по каждому из этих слов по отдельности выдаёт ссылки на страницы, которые содержат только одно соответствующее слово. Но есть и такие страницы, которые содержат и то, и другое слово вместе.

Справочная информация

Изобразим множества этих страниц при помощи диаграммы ( кругов Эйлера ). Множества страниц, содержащих слова «красный» и «синий», частично пересекаются.

синий

красный

Рассмотрим запрос « красный & синий ». Это те страницы, которые одновременно содержат слова и «красный» и «синий». На диаграмме это будет область, соответствующая пересечению множеств.

синий

красный

Операция логическое И (&) приводит к уменьшению количества найденных страниц.

Рассмотрим запрос «красный | синий» . Это те страницы, которые содержат или только слово «красный», или только слово «синий», или слова «красный» и «синий» одновременно. На диаграмме это будет область, соответствующая объединению множеств.

синий

красный

Операция логическое ИЛИ ( | ) приводит к увеличению количества найденных страниц.

8-1

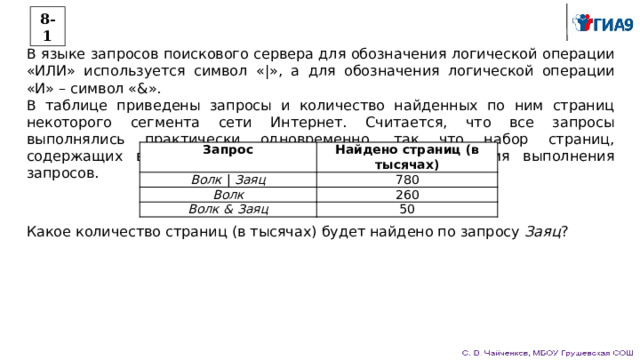
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Запрос

Найдено страниц (в тысячах)

Волк | Заяц

780

Волк

260

Волк & Заяц

50

Какое количество страниц (в тысячах) будет найдено по запросу Заяц ?

8-1

Запрос

Найдено страниц (в тысячах)

Волк | Заяц

780

Волк

260

Волк & Заяц

50

Какое количество страниц (в тысячах) будет найдено по запросу Заяц ?

Решение.

Используем графический способ решения с помощью кругов Эйлера.

Обозначим части кругов буквами и запишем соответствующие им значения по данным таблицы.

Волк | Заяц = a + b + c = 780

Волк = a + b = 260

Волк & Заяц = b = 50

Найти: Заяц = b + c = ?

Волк

Заяц

c

a

b

c = (a + b + c) – (a + b) = 780 – 260 = 520

b + c = 50 + 520 = 570

Ответ: 570.

8-2

Запрос

Найдено страниц (в тысячах)

Сканер | Принтер

140

Сканер

89

Принтер

65

Какое количество страниц (в тысячах) будет найдено по запросу Сканер & Принтер ?

Решение.

Используем графический способ решения с помощью кругов Эйлера.

Сканер | Принтер = a + b + c = 140

Сканер = a + b = 89

Принтер = b + c = 65

Найти: Сканер & Принтер = b = ?

Сканер

Принтер

c

a

b

c = (a + b + c) – (a + b) = 140 – 89 = 51

b = (b + c) – c = 65 – 51 = 14

Ответ: 14.

8-3

Запрос

Найдено страниц (в тысячах)

Футбол & Хоккей

120

Футбол

170

Хоккей

135

Какое количество страниц (в тысячах) будет найдено по запросу Футбол | Хоккей ?

Решение.

Используем графический способ решения с помощью кругов Эйлера.

Футбол

Футбол & Хоккей = b = 120

Хоккей

Футбол = a + b = 170

Хоккей = b + c = 135

Найти: Футбол | Хоккей = a + b + c = ?

c

a

b

c = (b + c) – b = 135 – 120 = 15

a + b + c = (a + b) + c = 170 + 15 = 185

Ответ: 185.

8-4

Запрос

Найдено страниц (в тысячах)

Лебедь & Рак

295

Лебедь & Щука

310

Лебедь & (Рак | Щука)

510

Какое количество страниц (в тысячах) будет найдено по запросу Лебедь & Рак & Щука ?

Решение.

Используем графический способ решения с помощью кругов Эйлера для трёх множеств.

Лебедь

Рак

Лебедь & Рак = b + e = 295

Лебедь & Щука = d + e = 310

Лебедь & (Рак | Щука) = b + d + e = 510

Найти: Лебедь & Рак & Щука = e = ?

c

a

b

e

f

d

d = (b + d + e) – (b + e) = 510 – 295 = 215

e = (d + e) – d = 310 – 215 = 95

g

Щука

Ответ: 95.