Презентация к уроку: "Экстремумы функции".

Тема : «Экстремумы функции».

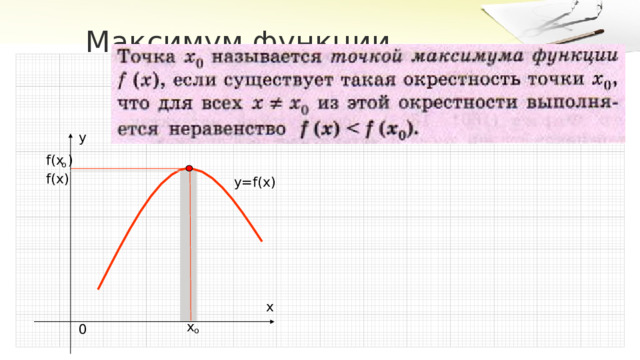
Максимум функции

y

f(х )

о

f(х)

y=f(x)

x

х

0

о

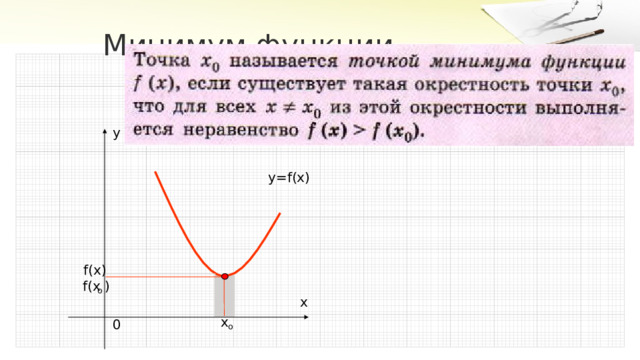
Минимум функции

y

y=f(x)

f(х)

f(х )

о

x

х

0

о

Точки минимума и максимума

называются точками экстремума функции.

Если х 0 - точка экстремума

дифференцируемой функции f(х),

то производная функции в

этой точке f ' (х 0 ) = 0.

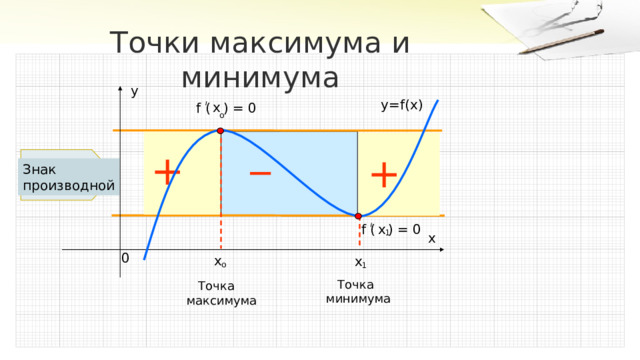
Точки максимума и минимума

y

y=f(x)

х

f ( ) = 0

о

_

+

+

Знак

производной

f ( ) = 0

х

1

x

0

х

х

о

1

Точка

минимума

Точка

максимума

Точки, в которых производная функции равна 0, называют стационарными точками .

х=0 – точка , в которой производная равна 0, но она не является точкой экстремума.

Точки, в которых функция имеет производную, равную 0 или не имеет производной, называют критическими точками.

х=0 – точка минимума, а производной в этой точке нет.

Задания ЕГЭ

На рисунке изображён график дифференцируемой функции  y = f ( x ) , определённой на интервале  (2 ; 13) .

Найдите точку из отрезка  [8 ; 12] ,  в которой производная функции  f ( x )  равна 0.

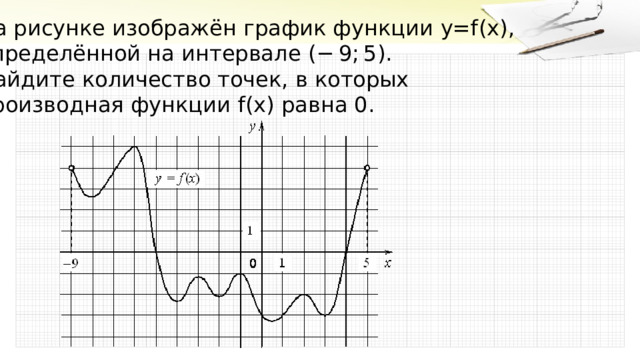
На рисунке изображён график функции  y = f ( x ) ,

определённой на интервале  (− 9; 5) .

Найдите количество точек, в которых

производная функции  f ( x )  равна 0.

На рисунке изображён график  y = f ′( x )   —  

производной функции  f ( x ) , определённой

на интервале  (−9; 8) . Найдите точку экстремума

функции  f ( x )  на отрезке  [−3; 3] .

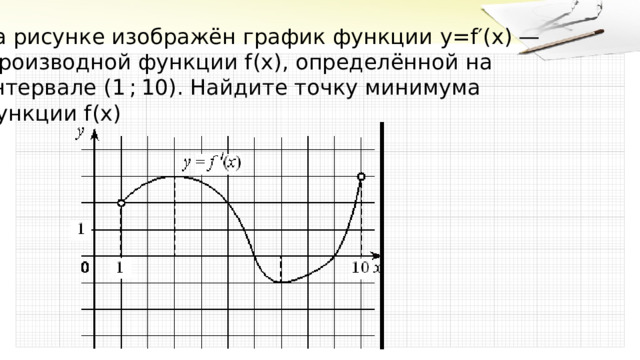
На рисунке изображён график функции  y = f ′( x )   —

  производной функции  f ( x ) , определённой на

интервале  (1 ; 10) . Найдите точку минимума  функции  f ( x )

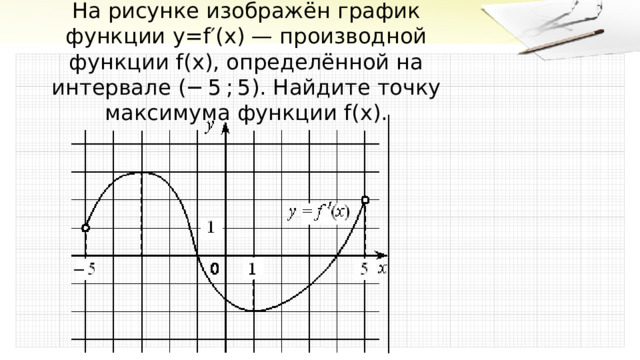
На рисунке изображён график функции  y = f ′( x )   —  производной функции  f ( x ) , определённой на интервале  (− 5 ; 5) . Найдите точку максимума функции  f ( x ) .

На рисунке изображён график функции  y = f ( x ) ,

определённой на интервале  (− 6 ; 6) . Найдите количество решений уравнения  f  '( x )=0  на отрезке  [− 4,5 ; 2,5] .

На рисунке изображён график  y = f  '( x )   —  

производной функции  f ( x ) , определённой на

интервале  (− 11 ; 6) . Найдите количество точек

минимума функции  f ( x ) , принадлежащих

отрезку  [− 6 ; 4] .

На рисунке изображён график  y = f  '( x )   —  

производной функции  f ( x ) , определённой на

интервале  (− 3 ; 19) . Найдите количество точек

максимума функции  f ( x ) , принадлежащих

отрезку  [− 2 ; 15] .

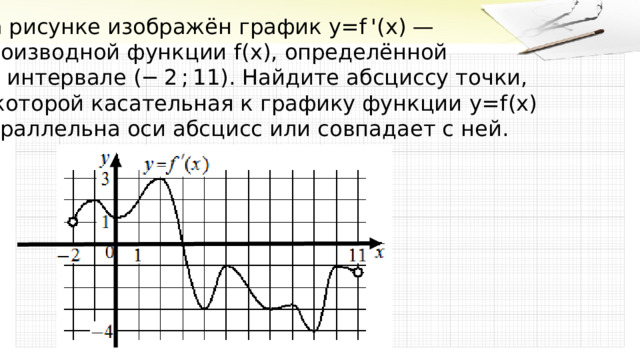
На рисунке изображён график  y = f  '( x )   —  

производной функции  f ( x ) , определённой

на интервале  (− 2 ; 11) . Найдите абсциссу точки,

в которой касательная к графику функции  y = f ( x )  

параллельна оси абсцисс или совпадает с ней.

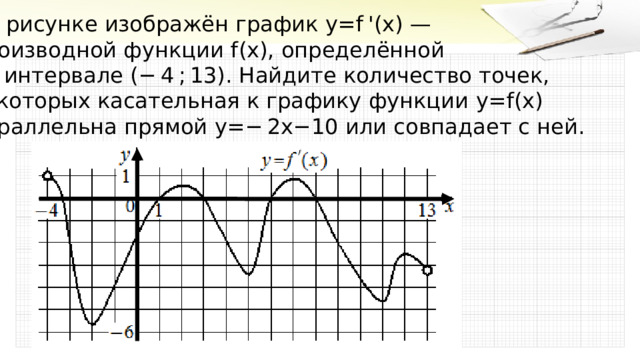
На рисунке изображён график  y = f  '( x )   —  

производной функции  f ( x ) , определённой

на интервале  (− 4 ; 13) . Найдите количество точек,

в которых касательная к графику функции  y = f ( x )  

параллельна прямой  y =− 2 x −10  или совпадает с ней.

Установите соответствие между графиками функций и характеристиками этих функций на отрезке [ − 1; 1 ] .

А)

Б)

1)функция возрастает на отрезке  [− 1; 1]

2)функция убывает на отрезке  [− 1; 1]

3)функция имеет точку минимума на отрезке  [− 1; 1]

4)функция имеет точку максимума на отрезке  [− 1; 1]

Г)

В)

Выполни!

Найдите точку максимума функции 

y = 10⋅ln( x −2) − 10 x + 11 .

Найдите точку максимума функции 

y = − 6 + 9 x + 5 .

Найдите точку минимума функции 

y = −28 x + 96⋅ln x + 31 .

Найдите точку минимума функции  y = 

Найдите точку минимума функции

y =(1−2 x )cos x + 2sin x + 7 , принадлежащую промежутку  ( 0 ;  ) .

Найдите точку минимума функции 

y = 1,5 − 30 x + 48⋅ln x + 4 .

Найдите точку максимума функции 

y = ​ ⋅ .

Найдите точку минимума функции 

y = ​ ⋅ ( x + 4) + 2 .

Найдите точку минимума функции 

y = () ⋅ .

Найдите точку максимума функции

y = ln −7x − 9.

Самостоятельная работа

1 вариант

1.Найдите точку минимума функции y =− 4 + 4x + 17

2.Найдите точку максимума функции y =11⋅ln(x+4) −11x − 5

3.Найдите точку максимума функции y =

1.Найдите точку максимума функции у =+ + 36x +20

2.Найдите точку минимума функции y = 4x − ln(x+5) + 2

3.Найдите точку минимума функции y = (x + 7) 2 ​⋅(x +1) − 6

2 вариант