Презентация к уроку геометрии

ЧТОБЫ ПЕРЕВАРИВАТЬ ЗНАНИЯ, НАДО ПОГЛОЩАТЬ ИХ С АППЕТИТОМ» Анатоль Франс

«Призма»

№

1

Веришь ли ты, что

  1

многогранник, составленный из двух равных многоугольников А 1 А 2 …А п и В 1 В 2 …В п расположенных в параллельных плоскостях, и n параллелограммов, называется призмой. 

2

боковые ребра призмы равны и параллельны 

2 

3

4

  3

высота призмы равна ее боковому ребру 

призма называется правильной, если ее основания правильные многоугольники. 

5

у прямой призмы боковые ребра перпендикулярны основаниям

6

в наклонной призме боковые грани- прямоугольники

Е 1

D 1

А 1

С 1

В 1

Призма -многогранник, две грани которого

являются равными многоугольниками,

лежащими в параллельных плоскостях, а остальные

грани - параллелограммами, имеющими общие

стороны с этими многоугольниками.

Е

D

А

С

В

Е 1

D 1

А 1

С 1

В 1

Основания

Боковая грань

Е

D

А

С

В

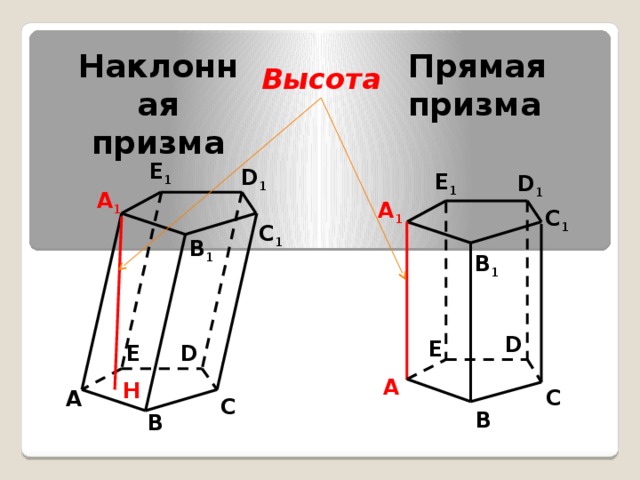
Наклонная призма

Прямая призма

Высота

Е 1

D 1

Е 1

D 1

А 1

А 1

С 1

С 1

В 1

В 1

D

Е

Е

D

А

H

С

А

С

В

В

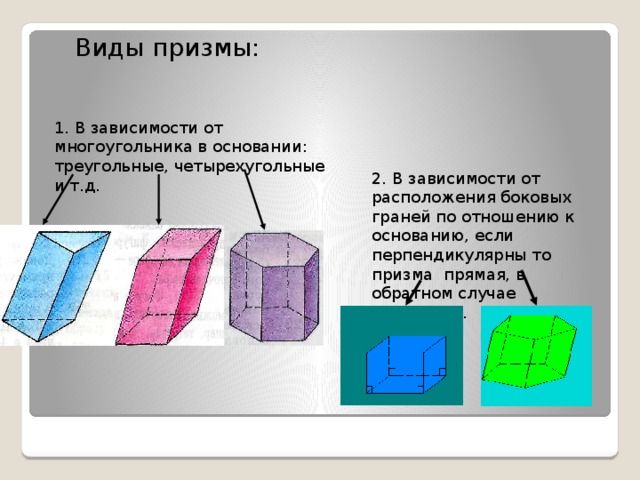
Виды призмы:

1. В зависимости от многоугольника в основании: треугольные, четырехугольные и т.д.

2. В зависимости от расположения боковых граней по отношению к основанию, если перпендикулярны то призма прямая, в обратном случае наклонная.

Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

Параллелепипед

(частный случай призмы)

Прямой

Наклонный

(боковое ребро перпендикулярно плоскости основания)

(боковое ребро не перпендикулярно плоскости основания)

Прямоугольный

( - прямой параллелепипед;

- основание – прямоугольник )

Куб

Задание 2. На столах модели призм. Измерить их элементы линейкой и заполнить таблицу:

Элементы:

Модель №1

a

Модель №2

b

h

P осн.

S осн.

S б.п.

S п.п.

Задание 2. Проверим задание:

Элементы:

Модель №1

a

Модель №2

4 см

b

4 см

4 см

h

4 см

8 см

P осн.

12 см

S осн.

8 см

16 см

7 см 2

S б.п.

96 см 2

16 см 2

S п.п.

128 см 2

110 см 2

160 см 2

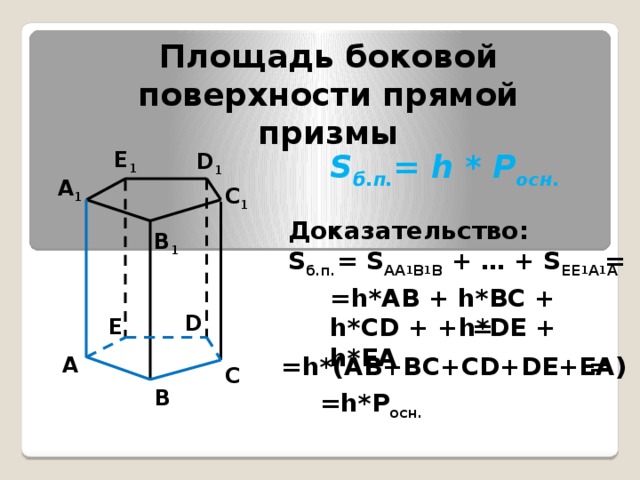
Площадь боковой поверхности прямой призмы

S б.п. = h * P осн.

Е 1

D 1

А 1

С 1

Доказательство:

S б.п. = S AA 1 B 1 B + … + S EE 1 A 1 A

В 1

=

=h*AB + h*BC + h*CD + +h*DE + h*EA

D

=

Е

=h*(AB+BC+CD+DE+EA)

=

А

С

В

=h*Р осн.

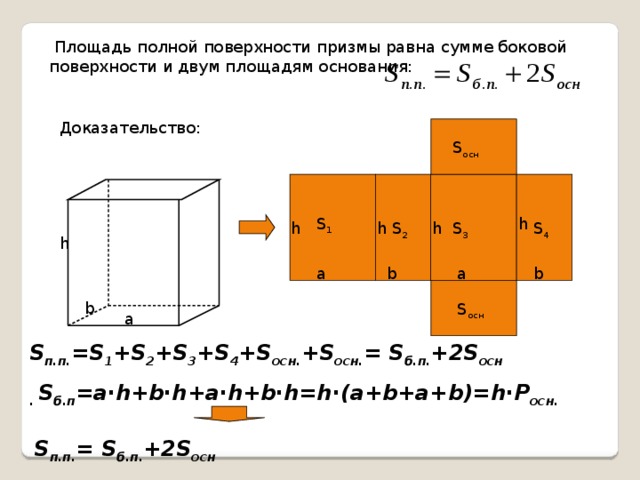
Площадь полной поверхности призмы равна сумме боковой поверхности и двум площадям основания:

Доказательство:

S осн

h

S 1

h

h

h

S 2

S 3

S 4

h

а

а

b

b

b

S осн

а

S п.п. =S 1 +S 2 +S 3 +S 4 +S осн. +S осн. = S б.п. +2S осн

. S б.п =a ∙h+b∙h+a∙h+b∙h=h∙(a+b+a+b)=h∙P осн.

S п.п. = S б.п. +2S осн

• Что нового вы узнали на уроке?

2. Что использовали для «открытия»

новых знаний?

3. Вы достигли поставленной цели?

4. Как вы оцените свою работу на уроке?

Спасибо за урок!