Презентация к уроку геометрии на тему "Свойства высот треугольника"

Тема урока: «Серединный перпендикуляр к отрезку. Свойство серединного перпендикуляра к отрезку

Презентация выполнена учителем математики МОАУ «СОШ № 27 г.Орска»

Левшиной О.А.

Тема урока : Серединный перпендикуляр к отрезку. Свойство серединного перпендикуляра к отрезку.

• Цели урока :
• Предметные   - ввести понятие серединного перпендикуляра к отрезку; рассмотреть теорему о серединном перпендикуляре и следствие из него.
• Личностные   - формировать интерес к изучению темы и желание применять приобретённые знания и умения.
• Метапредметные  -формировать умение использовать приобретённые знания в практической деятельности.
• Задачи: 1) Развивать критичность мышления, способность к эмоциональному восприятию математических задач, решений, рассуждений;
• 2) доказать теорему о серединном перпендикуляре;
• 3) показать применение теоремы о серединном перпендикуляре при решении задач.
•  

Решить устно:

1 ) Найти: S АВЕ .

) ВМ = m ,

АВС = α.

Найти расстояние от точки М до прямой АС .

• Геометрия - удивительная наука. Её история насчитывает не одно тысячелетие, но каждая встреча с ней способна одарить и обогатить волнующей новизной маленького открытия, изумляющей радостью творчества. Действительно, любая задача элементарной геометрии является, по существу, теоремой, а ее решение – скромной (а иногда и огромной) математической победой.
• Сегодня мы продолжим изучение темы «Замечательные точки треугольника» и познакомимся с серединным перпендикуляром к отрезку.

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему .

• a

• A

• B

• O

• a

Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Дано: М - произвольная точка а,

а- серединный перпендикуляр к отрезку АВ.

Доказать:

МА=МВ

Доказательство:

• Если М  АВ, то М совпадает с

точкой О  МА=МВ.

2) Если М  АВ, то  АМО=  ВМО по двум катетам (АО=ВО, МО- общий катет)  МА=МВ.

• М

• B

• А

• O

• O

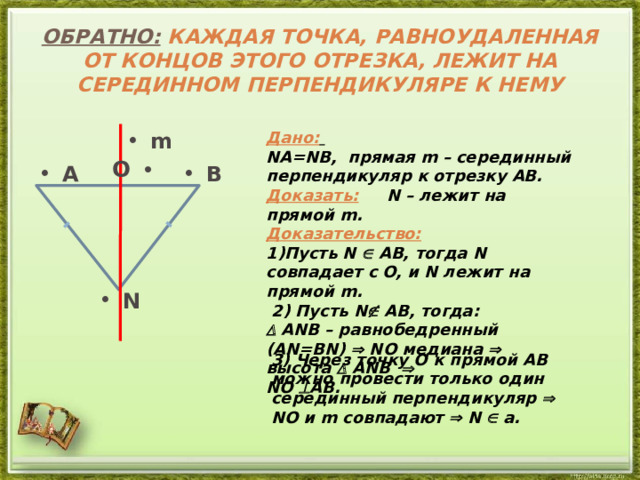
Обратно: Каждая точка, равноудаленная от концов этого отрезка, лежит на серединном перпендикуляре к нему

Дано:

• m

NА=NВ, прямая m – серединный перпендикуляр к отрезку АВ.

Доказать: N – лежит на прямой m.

Доказательство:

1)Пусть N  АВ, тогда N совпадает с O, и N лежит на прямой m.

2) Пусть N  АВ, тогда:

 АNВ – равнобедренный (AN=BN)  NO медиана  высота  АNВ 

NO  AB.

• B

• А

• N

3) Через точку О к прямой АВ можно провести только один серединный перпендикуляр 

NO и m совпадают  N  а.

Следствие: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Дано:

m  AC, n  BC, AM=MC, CN=NB.

Доказать: O= m  n  p.

Доказательство:

1) Предположим: m║n,

тогда: AC  m и AC  n,

что невозможно.

2) По доказанному:

OC=OA и OC=OB 

OA=OB,  т.O  p 

O= m  n  p.

• С

• m

• n

• М

• N

• О

• В

• А

• P

• p

• Домашнее задание: вопросы 17–19, с. 187–188; №№ 680 (б), 681, 686 (задача решена в учебном пособии).
•