Презентация к уроку геометрии "Решение треугольников"

Решение треугольников

Геометрия 9 класс

Цель урока:

• научиться решать произвольные треугольники

Вопросы

• 1. Какую фигуру называют треугольником?
• 2. Перечислите элементы треугольника.
• 3. Назовите виды треугольников по углам.
• 4. Назовите виды треугольников по сторонам.
• 5. Как построить единичную полуокружность?
• 6. Объясните, что такое синус угла α из промежутка 0 0 ≤ α ≤ 180 0
• 7. Объясните, что такое косинус угла α из промежутка 0 0 ≤ α ≤ 180 0
• 8. Что называется тангенсом угла α?
• 9. Для какого значения тангенс α не определен и почему?
• 10. Назовите основное тригонометрическое тождество.
• 11. Сформулируйте теорему о площади треугольника.
• 12. Сформулируйте теорему синусов.
• 13. Сформулируйте теорему косинусов.
• 14. Сформулируйте теорему о сумме углов треугольника.
•  

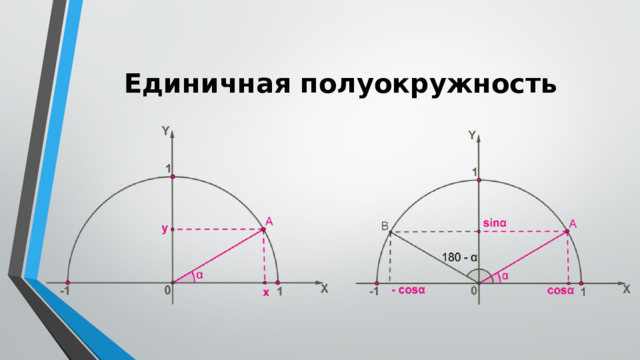
Единичная полуокружность

Определение

Решением треугольника называется нахождение всех его шести элементов (то есть трёх сторон и трёх углов) по каким-нибудь трём данным элементам.

В

c

a

С

А

b

Для этого вспомним

Решение данных задач основано на использовании теорем синуса и косинуса, теоремы о сумме углов треугольника и следствии из теоремы синусов: в треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.

Причем, при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов.

Соотношения между сторонами и углами в треугольнике

Сумма углов треугольника

Сумма углов треугольника равна 180 º

В

С

А

РЕШЕНИЕ ТРЕУГОЛЬНИКОВ

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов

В

c

a

С

А

b

9

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

В

c

a

С

А

b

Три задачи на решение треугольника

Рассмотрим 3 задачи на решение треугольника:

• решение треугольника по двум сторонам и углу между ними;
• решение треугольника по стороне и прилежащим к ней углам;
• решение треугольника по трем сторонам.

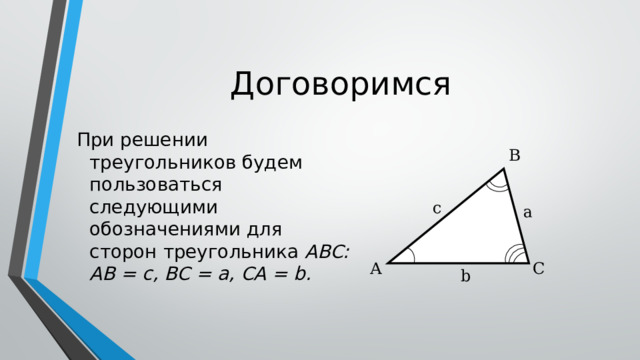
Договоримся

При решении треугольников будем пользоваться следующими обозначениями для сторон треугольника ABC: АВ = с, ВС = а, СА = b.

В

c

a

А

С

b

B

Решение треугольников

c

a

По двум сторонам

и углу между ними

Дано :

Найти:

Решение:

1.

2.

3.

Или

2.

3.

C

A

b

По трем сторонам

Дано :

Найти:

Решение:

1.

2.

3.

По стороне и

прилежащим к ней углам

Дано :

Найти:

Решение:

1.

2.

3.

Или

3.

1. Найти: BC

B

?

6

120 0

C

A

6

Ответ:

2 . Найти:

B

?

4

2

C

A

Ответ:

3.Найти: BС

B

60 0

?

45 0

C

A

4

Ответ:

4. Найти :

B

135 0

?

C

A

2

Ответ:

Найти:

cos

12

5

13

cos

Ответ:

Самостоятельная работа

Ответы к задачам самостоятельной работы

Из истории математики

• Термин «тригонометрия» дословно означает «измерение треугольников». Его ввел в употребление в 1595 году немецкий математик и богослов Питиск, автор учебника по тригонометрии и различных таблиц.
• Тригонометрия – раздел математики, который изучает зависимость между углами и сторонами треугольника.
• Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. А в Древней Греции во 2 веке до н.э. астроном Гиппарх из Никеи составил таблицу для определения соотношений между элементами треугольника. По существу это была первая таблица синусов.

Из истории математики

• К концу 13 века ученые исламского мира уже оперировали тригонометричес-кими функциями, открыли и доказали несколько важных теорем, использовали окружность единичного радиуса. Арабские математики составили исключительно точные таблицы синусов и тангенсов с шагом в 1′.
• Особенно большое влияние на развитие тригонометрии оказал «Трактат о полном четырех-угольнике» астронома

Насир ад-Дин ат-Туси.

• Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная наука.

Насир ад-Дин ат-Туси

( 1201 -1274)

Из истории математики

• Трактат Ат-Туси произвел огромное впечатление на немецкого астронома и математика Иоганна Мюллера (1436-1476). Современники больше знали его под другим именем. Это имя переводится на латинский язык как название его родного города Кёнигсберга.
• Иоганн Мюллер – автор первых печатных астро-номических таблиц, где применялись триго-нометрические знания, которыми пользовались Васко да Гама, Христофор Колумб и другие мореплаватели.

Иоганн Мюллер

(1436—1476)

• Труд Региомонтана «О треугольниках всех родов пять книг» сыграл в европейской математике огромную роль – дал толчок к бурному развитию тригонометрии в Европе. Дальнейшее ее развитие пошло по пути накопления и систематизации формул, уточнение основных понятий, становления терминологии и обозначений.
• Региомонтан основал одну из первых астрономических обсерваторий в Европе (г. Нюрнберг, 1471г.)

Измерительные работы

Тригонометрические функции могут быть использованы для проведения различных измерительных работ на местности.

Об этом мы поговорим на следующем уроке.

Решение задачи с практическим содержанием.

• На судна “Стремительный” и “Быстрый” поступил сигнал бедствия с судна “Звезда” .Радиопеленгатор судна “Стремительный” определил пеленг в 55 0 , а судна “Быстрый” - 100 0 .Кто первым придет на помощь “Звезде”, если скорость “Стремительного” равна
• 60 км/ч, а “Быстрого”- 45 км/ч?

Проведение спасательных операций

Звезда

С

sos

sos

Стремительный

60 км/ч

Быстрый

А

45 км/ч

20 км

Закончим урок словами великого итальянского ученого Галилео Галилея:

• “ Геометрия является самым могущественным средством

для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать”.

Синквейн

• 1.Треугольник
• 2.Остроугольный, тупоугольный
• 3. Строим, решаем, анализируем.
• 4.Любовный треугольник
• 5. Геометрическая фигура

Дополнительные задачи

№ 1

Найдите ВС

Какую теорему использовали?

D

8

0

45

B

Ответ:

?

0

30

теорема синусов

C

№ 2

Найдите АВ

Какую теорему использовали?

B

5

?

о

60

10

Е

А

Ответ:

теорема косинусов

Найдите Sinβ -?

Какую теорему использовали?

№ 3

К

9

45 о

Ответ:

12

С

А

теорема синусов

Sinβ -?