© 2021 1473 215
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 13.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Презентация "Логарифмическая функция"
Категория:
Математика
11.01.2021 13:26
Просмотр содержимого документа
«Презентация "Логарифмическая функция"»
Логарифмическая функция
0 и а ≠ 1), называют логарифмической функцией с основанием а " width="640"
Определение логарифмической функции
Функцию, заданную формулой
y = log a x (где а 0 и а ≠ 1),
называют логарифмической функцией с основанием а
Построить графики функций
y = log 2 x и y = log 1/2 x
x
¼
y = log 2 x
½
-2
1
-1
2
0
4
1
2
8
3
x
y = log 1/2 x
¼
½
2
1
1
0
2
-1
4
-2
8
-3
y
3
2
1
x
0
4
1
2
- 1
8
- 2
- 3
1. у 1. D(f) =(0;+∞) 2. E(f) =R 3. Функция является ни четной, ни нечетной 4. Проходит через точку (1;0) 5. Промежутки знакопостоянства: у 0 при x € (1; +∞) у 6. Функция возрастает при x € (0; +∞). 7. Функция непрерывна. х 1 " width="640"
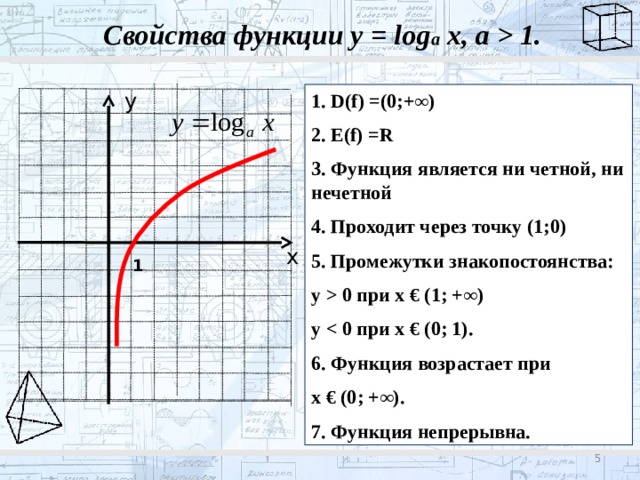
Свойства функции у = log a x, a 1.
у
1. D(f) =(0;+∞)
2. E(f) =R
3. Функция является ни четной, ни нечетной
4. Проходит через точку (1;0)
5. Промежутки знакопостоянства:
у 0 при x € (1; +∞)
у
6. Функция возрастает при
x € (0; +∞).
7. Функция непрерывна.
х
1
0 при x € (0; 1) у 6. Функция убывает при x € (0; +∞). 7. Функция непрерывна. х 1 5 " width="640"
Свойства функции у = log a x, 0
у
1. D (f) =(0;+∞)
2. E (f) =R
3. Функция является ни четной, ни нечетной
4. Проходит через точку (1;0)
5. Промежутки знакопостоянства:
у 0 при x € (0; 1)
у
6. Функция убывает при
x € (0; +∞).
7. Функция непрерывна.
х
1
5
Определите, какие из перечисленных ниже функций являются возрастающими, а какие убывающими:
1) y = log 3 x;
2) y = log 2 x;
3) y = log 0,2 x;
4) y = log 0,5 (2x+5);
5) y = log 3 (x+2)
6
физкультминутка
6
6
Используя свойства
логарифмической функции, сравнить:
а) lоg 2 3 и log 2 5;
б) log 2 1/3 и log 2 1/5;
в)log 1/2 3 и log 1/2 5;
г)log 1/2 1/3 и log 1/2 1/5.
6
Блиц - опрос
1. Область определения логарифмической функции – вся числовая прямая, а область значений этой функции – промежуток (0, + ∞).
2. Монотонность логарифмической функции зависит от основания логарифма.
3. Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
4. Логарифмическая функция является ни чётной, ни нечётной.
5. Логарифмическая функция непрерывна.
6
Взаимопроверка :
1
2
нет
3
да
4
нет
5
да
да
6
Рефлексия
Вы считаете, что урок прошел плодотворно, с пользой.
Вы научились и можете помочь другим.
Я доволен
Вы считаете, что научились, но вам еще нужна помощь.
собой!
Я вполне
Вы считаете, что было трудно на уроке.
доволен
Мне нужна
собой!
помощь!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
