Презентация "Методы решения экономических задач"

Цель проекта: Классифицировать и систематизировать виды экономических задач.

Научиться решать экономические задачи.

Создать методическое пособие для учащихся 10-11 классов при подготовке к ЕГЭ.

Задачи проекта:

• Изучить теоретический материал в рамках

подготовки ЕГЭ.

• Проанализировать виды экономических задач,

которые встречаются в ЕГЭ.

• Развить умение применять полученные знания

при решении экономических задач

Объект исследования: КИМы из сборников для подготовки к ЕГЭ 2015-2018 учебные года.

Предмет исследования:

экономические задачи

Методы исследования: анализ литературы, анкетирование, обобщение, синтез.

Актуальность работы заключается в том,

что благодаря грамотной классификации

и знаниям основных формул и приемов

практически каждый выпускник сможет

Решить экономическую задачу на ЕГЭ.

План работы:

• Работа с литературой
• Провести анкетирование учащихся
• Изучение видов задач на проценты
• Изучение способов решения задач

• Составить сборник экономических задач и задач на оптимизацию по математике

•   Выводы

Итоги анкетирования

1.Плохое знание теоретического материала

- 7 человек

2. Недостаточность навыка решения

экономических задач

- 6 человек

3. Большая затрата времени на решение

экономических задач

-12 человек

4. Малое количество часов на изучение этой

темы в школе

- 5 человек

5.Трудность задач - 15 человек

Гипотеза:

Результаты анкетирования позволяют мне предположить, что если мне удастся изложить теоретический и практический материал, необходимый для решения экономических задач, в доступной для каждого выпускника форме, количество учащихся справившихся с этим видом задач возрастет.

Основные ошибки:

• – неверное составление модели;

• – вычислительные (арифметические);
• – прекращение решения без доведения ответа

до числового значения;

• – не доведение решения до конца из-за невнимательного прочтения вопроса;
• – решение методом подбора без обоснования;
• – применение готовых формул для задач о кредитовании, отсутствующих в учебниках

3 правила, упрощающие решение

3 правила, упрощающие решение

1. Для упрощения записей и вычислений при решении задач о вкладах, кредитах и оптимизацию производства переходить от «языка процентов» к десятичным дробям . Например, «увеличение величины на 15%» равносильно её умножению на число 1,15 (так как 100% + 15% = 115% = 1,15); «уменьшение величины на 24%» равносильно её умножению на число 0,76 (так как 100% - 24% = 76% = 0,76).

3 правила, упрощающие решение

3 правила, упрощающие решение

2. Для правильного выбора способа решения необходимо уметь выделять основные типы задач :

• задачи о вкладах;
• задачи о кредитах (аннуитетные и дифференцированные)
• задачи на оптимизацию

3 правила, упрощающие решение

3. Большинство задач следует сначала решать «в общем виде» , вводя следующие обозначения:

• S – сумма вклада или кредита;
• x – ежемесячный вклад или ежемесячная выплата;
• n – срок (количество месяцев или лет);
• r % - процентная ставка;
• – множитель для вычисления процентных начислений ;

числовые данные подставлять только по окончании всех преобразований

Предположим, кто то взял кредит на 1 млн руб под 30% годовых

Долг % Долг с %

1 000 000 + 300 000 = 1 300 000

100% 30% 130%

Если долг увеличивается на 30%, это значит, что он становится равен 130% от суммы до начисления. Значит чтобы найти сумму после начисления надо сумму до начисления умножить на 1,3

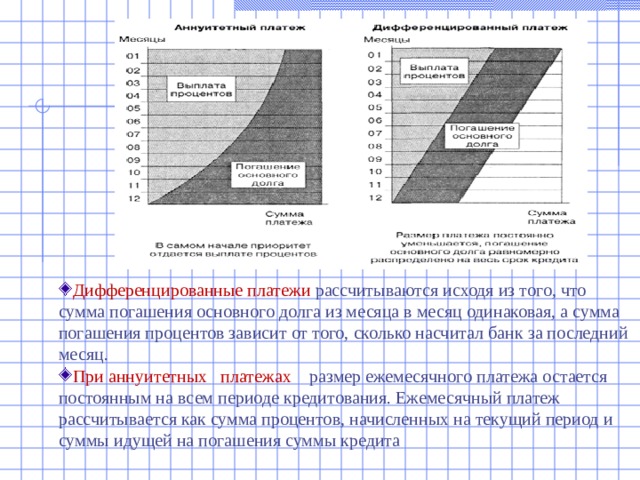
• Дифференцированные платежи  рассчитываются исходя из того, что сумма погашения основного долга из месяца в месяц одинаковая, а сумма погашения процентов зависит от того, сколько насчитал банк за последний месяц.
• При аннуитетных платежах размер ежемесячного платежа остается постоянным на всем периоде кредитования. Ежемесячный платеж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита

Задача 1 (дифференнцированный)

• Допустим, что в банке взят кредит 1200 рублей на 12 месяцев. Причем, каждый платежный период долг сначала возрастает на 10% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же величину меньше долга на конец предыдущего платежного периода. Необходимо ответить на вопросы: Какую сумму нужно вернуть банку за весь платежный период? Какова сумма переплаты?

Долг перед банком по состоянию на конец года должен уменьшаться до нуля равномерно, то есть последовательность долгов перед банком такова:

1200;1100; 1000; 900;800; 700; 600; 500; 400; 300; 200;100.

Первого числа каждого месяца долг возрастает на 10% . Тогда последовательность долгов будет такова:

1200∙1.1; 1100∙1.1; 1000∙1.1; 900∙1.1; 800∙1.1; 700∙1.1; 600∙1.1; 500∙1.1; 400∙1.1; 300∙1.1; 200∙1.1;100∙1.1.

или

1320; 1210; 1100;990; 880; …110.

Обращаем внимание на то, разница между долговыми суммами равна 110 рублей . (1320-1210=110)

Теперь найдем ежемесячные выплаты:

1 месяц- 1320-1100=220

2 месяц- 1210-1000=210

3 месяц- 1100- 900=200

4 месяц- 990- 800=190

5 месяц – 880-700=180 и так далее. И последняя наименьшая выплата равна 110 рублей . Замечаем, что выплаты уменьшаются ежемесячно на 10 рублей .

Такова схема дифференцированного платежа.

Далее можно найти сумму всех выплат. Она равна: 220+210+200+…+110 = 1980 (рублей).

Таким образом, переплата составляет 65%. ((1980*100):1200=165%)

В общем виде задача формулируется так: 31 декабря 2014 года Андрей взял в банке S рублей в кредит под a процентов годовых. Схема выплаты кредита следующая: 1 числа каждого следующего года банк начисляет a процентов на оставшуюся сумму долга. Затем Андрей переводит в банк сумму X ежегодного платежа (транш). Весь долг Андрей должен выплатить за n лет, то есть за n равных платежей. Необходимо найти одну из неизвестных величин: S , a , X, или n .

Задача 2 (аннуитетный)

• 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:

-1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего года.

-со 2го по 14е число каждого месяца необходимо выплатить часть долга.

-15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей

дата

15.01

Долг(млн в рублей)

15.02

1

15.03

0,6

15.04

0,4

15.05

0,3

15.06

0,2

15.07

0,1

0

• Найдите наибольшее значение r , при котором общая сумма выплат будет составлять менее 1,2 млн рублей .

Долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом: 1; 0.6; 0.4; 0.3; 0.2; 0.14; 0. Обозначим k = 1+ Тогда долг на 1-е число каждого месяца равен: 1к; 0.6к; 0.4к; 0.3к; 0.2к; 0.1к; 0к Найдем теперь выплаты со 2-е по 14-е число каждого месяца: 1к-0.6; 0.6к-0.4; 0.4к-0.3; 0.3к-0.2; 0.2к-0.1; 0.1к-0; Общая сумма выплат составляет: 1к-0.6+ 0.6к-0.4+0.4к-0.3+ 0.3к-0.2+ 0.2к-0.1+0.1к-0=2.6к-1.6 По условию, общая сумма выплат будет меньше 1,2 млн руб. Значит, составляем неравенство: 2.6к-1.6≤ 1.2 . Отсюда к ≤ Подставляя вместо k выражение 1+ и решая неравенство, получим, что r ≤ 7 Наибольшее целое решение этого неравенства – число 7. Значит, искомое число процентов - 7%.

• Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров . Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров . Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

1-й способ – с помощью логики и арифметических действий.

Найдем стоимость 1 номера стандартного:

2000:21=95 (рублей).

Найдем стоимость 1 номера «люкс»:

4500: 49 =91 (рублей).

Так как стоимость 1 стандартного номера дороже, то выгоднее разместить на этой площади больше номеров стандартных, и как можно меньше номеров «люкс».

Начнем перебор количества номеров «люкс» с наименьшей цифры.

Пусть номеров «люкс» будет 0. Тогда число 1099 не делится нацело на 21. Далее.

Допустим, что номеров «люкс» будет 1. Тогда: 1099- 49=1050 ;

1050: 21 = 50 (номеров стандартных). Значит, на площади 1050 можно разместить 50 стандартных номеров. Тогда в сутки отель может заработать: 50∙ 2000 + 1∙ 4500=104500 (р.)

2-й способ – с помощью составления опорной линейной функции.

Пусть х – количество стандартных номеров,

у- количество номеров «люкс».

Они занимают площадь 21х+49у.

Составим равенство: 21х+49у = 1099.

Выразим из этого равенства у = .

Составим функцию заработанных денег:

S ( x , y ) =2000∙ x + 4500∙ y .

Далее подставим в эту функцию выражение для у.

Получим S ( x ) =71 ∙х + 4500∙22 .

Это возрастающая линейная функция.

Свое наибольшее значение она принимает при наибольшем значении х и наименьшем значении у.

По условию х и у – натуральные числа.

Значит, у=1 (это наименьшее натуральное число) и х=50. Значит, S = 2000∙50 + 4500∙ 1=104500.

Заключение

В результате данной работы я:

– смогла все экономические задачи разбить на три основных группы;

– решила ряд экономических задач;

– создала методическое пособие для учащихся 10-11 классов при подготовке к ЕГЭ.

Для успешной сдачи надо помнить, что все экономические задачи в вариантах ЕГЭ вычислительные, поэтому для их успешного решения должен быть отработан аппарат стандартных вычислений.

Благодаря полученным знаниям в процессе моей работы, экономические задачи стали для меня не проблемой. Теперь я с легкостью смогу решить экономическую задачу на ЕГЭ и получить 3 балла, ведь для математики 3 балла – это очень много.

Экономические задачи – это не просто задачи из математики, это часть нашей жизни в современном мире. Умение их решать будет полезно как для проверки банковских операций, так и в простых жизненных ситуациях.

Спасибо за внимание !