Презентация на тему : Методы решений тригонометрических уравнений.

Методы решения тригонометрических уравнений

Содержание

• Метод замены переменной
• Метод разложения на множители
• Однородные тригонометрические уравнения
• С помощью тригонометрических формул:

• Формул сложения
• Формул приведения
• Формул двойного аргумента

Метод замены переменной

С помощью замены t = sinx или t = cosx, где t ∈ [−1;1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения.

См. примеры 1 – 3

Иногда используют универсальную тригонометрическую подстановку: t = tg

x

2

Пример 1

Пример 2

Пример 3

Метод разложения на множители

Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл:

f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0

и т.д. при условии существования каждого из сомножителей

См. примеры 4 – 5

Пример 4

Пример 5

Однородные тригонометрические уравнения

Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени .

: cos x

a sin x + b cos x = 0

a sin x b cos x 0

=

+

cos x

cos x

cos x

a tg x + b = 0

b

tg x = –

a

Замечание.

Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0 .

Однородные тригонометрические уравнения

Уравнение вида a sin 2 x + b sin x cos x + c cos 2 x = 0 называют однородным тригонометрическим уравнением второй степени .

: cos 2 x

a sin 2 x + b sin x cos x + c cos 2 x = 0

a sin 2 x b sin x cos x c cos 2 x 0

+

=

+

cos 2 x

cos 2 x

cos 2 x

cos 2 x

a tg 2 x + b tg x + c = 0

Далее, вводим новую переменную tg x = t и решаем методом замены переменной.

Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения

на множители.

Пример 7

Пример 6

Пример 8

Пример 9

Пример 10

Пример 11

С помощью тригонометрических формул

1. Формулы сложения :

sin (x + y) = sinx cosy + cosx siny

sin (x − y) = sinx cosy + cosx siny

cos (x + y) = cosx cosy − sinx siny

cos (x − y) = cosx cosy + sinx siny

tgx + tgy

сtgx сtgy − 1

сtg (x + y) =

tg (x + y) =

сtgу + с tgх

1 − tgx tgy

tgx − tgy

сtgx сtgy + 1

tg (x − y) =

сtg (x − y) =

сtgу − с tgх

1 + tgx tgy

Пример 12

Пример 13

С помощью тригонометрических формул

2. Формулы приведения:

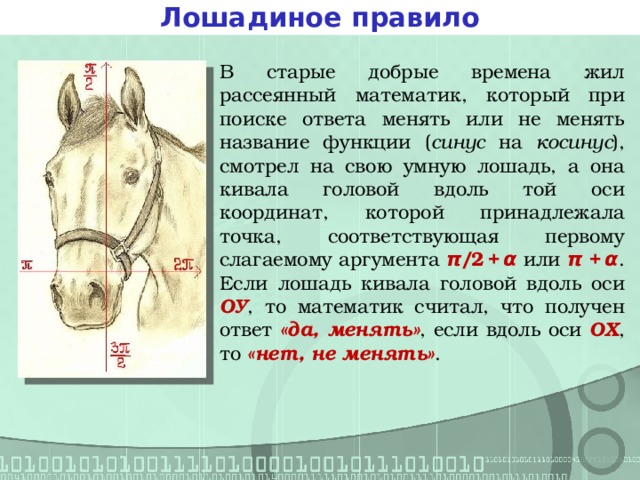
Лошадиное правило

В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции ( синус на косинус ), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α .

Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять» .

С помощью тригонометрических формул

3. Формулы двойного аргумента :

sin 2x = 2sinx cosx

cos 2x = 2cos 2 x – 1

cos 2x = cos 2 x – sin 2 x

cos 2x = 1 – 2sin 2 x

2tgx

tg 2x =

1 – tg 2 x

ctg 2 x – 1

ctg 2x =

2ctgx

Пример 14

С помощью тригонометрических формул

4 . Формулы понижения степени:

5. Формулы половинного угла:

С помощью тригонометрических формул

6. Формулы суммы и разности :

С помощью тригонометрических формул

7. Формулы произведения :

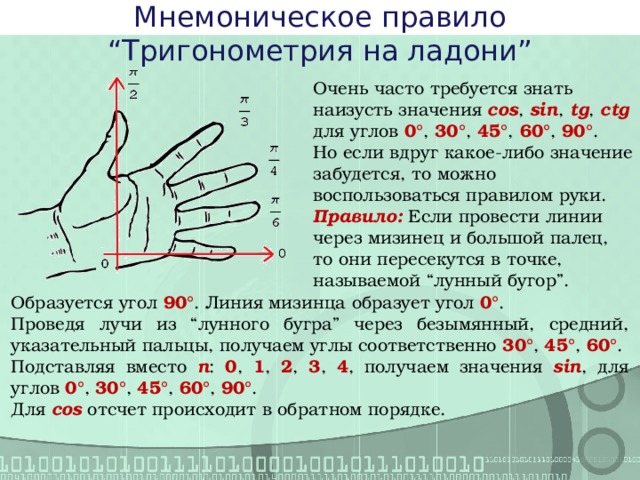
Мнемоническое правило “Тригонометрия на ладони”

Очень часто требуется знать наизусть значения cos , sin , tg , ctg для углов 0° , 30° , 45° , 60° , 90° .

Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки.

Правило: Если провести линии через мизинец и большой палец,

то они пересекутся в точке, называемой “лунный бугор”.

Образуется угол 90° . Линия мизинца образует угол 0° .

Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30° , 45° , 60° .

Подставляя вместо n : 0 , 1 , 2 , 3 , 4 , получаем значения sin , для углов 0° , 30° , 45° , 60° , 90° .

Для cos отсчет происходит в обратном порядке.

22