Презентация по алгебре на тему "Линейная функция и её график". 1 урок.

Линейная функция и её график

0; при k" width="640"

1) Что является графиком функции у=кх ?

2) Что называют угловым коэффициентом прямой у=кх?

3) Какой угол с осью х образует прямая у=кх при к0; при k

1 . Какие из функций являются прямой пропорциональностью.

4) y=-5x

5) y=

6) y =

1) y=17x

2) y=

3) y =

2. В каких координатных четвертях проходит график функции

3) у= -7,8х

4) y=

1) y= 50x

2) y= -

Функция вида y = kx +b , где k и b числа, а x и y переменные, называется линейной функцией.

x – независимая переменная (аргумент)

y – зависимая переменная (функция)

Графиком линейной функции y = kx + b является прямая линия

x

-2

Y

-1

0

1

2

4

1

7

-5

-2

y = 3x + 1

Через две точки можно провести только одну прямую линию

Для построения графика линейной функции достаточно двух точек!

«в горку»

«с горки»

Рассмотрим графики функций, изображенные на рисунках

y=kx+m

y=kx+m

(k  0)

(k  0)

Если k  0, то линейная функция

y = k x + m возрастает

Если k  0, то линейная функция y = k x + m убывает

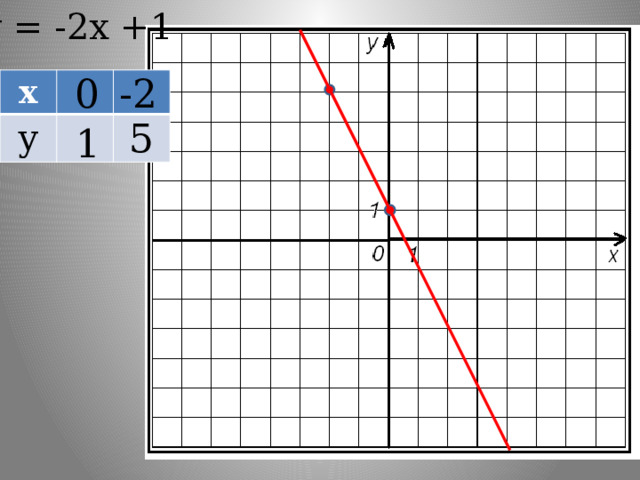
у = -2х +1

0

-2

х

у

5

1

у = 2х - 5

0

3

х

у

-5

1

y= 0,5 х +2

k = 1

0

4

х

у

k = 4

2

4

k = 0,5

y= 4 х +2

1

0

х

у

6

2

y= х +2

3

0

х

у

Чем больше угловой коэффициент k , тем больше угол, образованный графиком функции с осью ОХ

2

5

Построим несколько графиков линейных функций, у которых одинаковые угловые коэффициенты.

у = -х + 4

-2

0

х

у

4

6

у = -х

0

-3

х

у

3

0

у = -х - 5

-6

0

х

у

Если у линейных функций угловой коэффициент одинаковый, то их графики параллельны !

-5

1

у = -3х + 4

0

-1

х

у

4

7

4

у = х + 4

0

2

х

у

4

6

у = 2х + 4

0

1

х

у

График линейной функции пересекает

ось OY в точке (0;b).

6

4

Домашнее задание:

П.6.3 стр.138;

Решить №384, 385 стр.140.