Презентация по теме "Элементарные функции и их графики"

ФУНКЦИИ И ИХ ГРАФИКИ

у х , х у.

х

Виды функций и построение графических образов:

1. Виды функций

• Степенная
• Показательная
• Логарифмическая
• Тригонометрическая

2. Построение графических образов

3. Тест

Виды функций

Y=x n

n – любое число

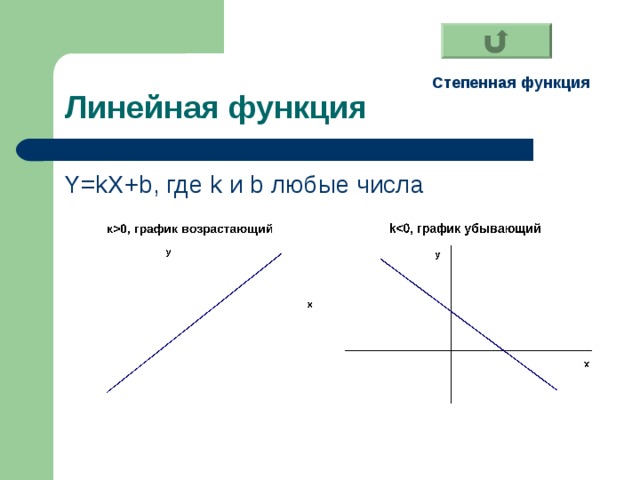
• Линейная
• Квадратичная
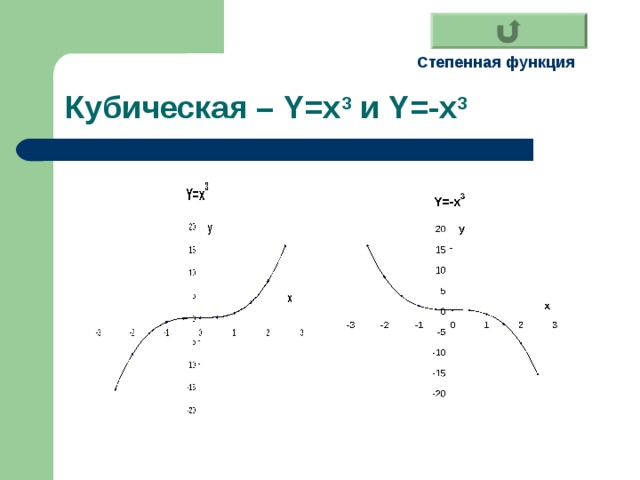
• Кубическая
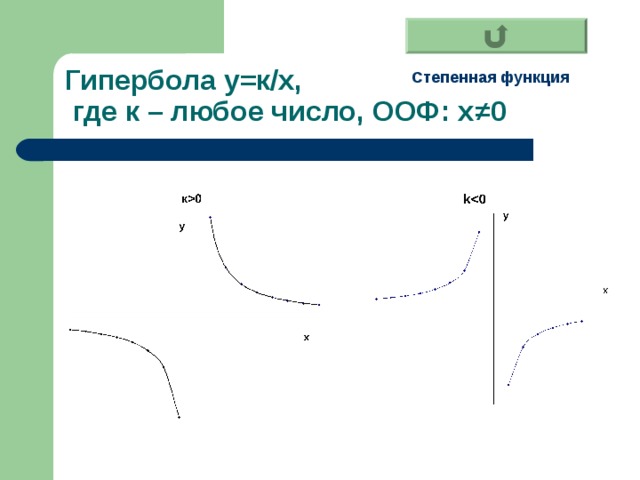
• Гипербола
• Y=X 1/2 и Y=-X 1/2
• Y=X 1/3 и Y=-X 1/3

Степенная функция

Y=kX+b , где k и b любые числа

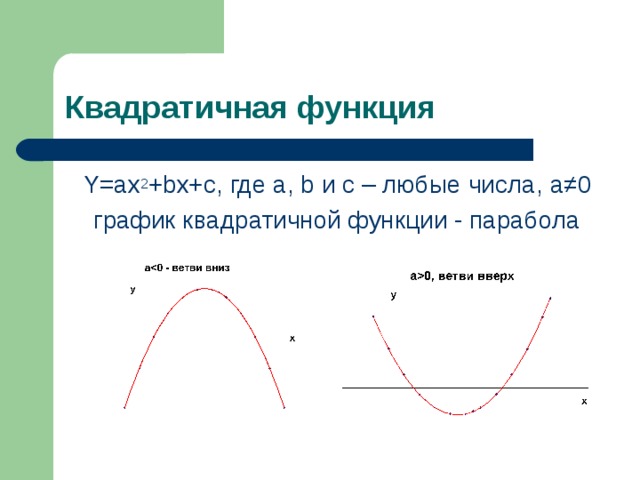
Y=ax 2 +bx+c , где a , b и с – любые числа, a ≠0

график квадратичной функции - парабола

Свойства функции Y=X 2 и Y= - X 2

• ООФ: (- ∞:∞)
• ОЗФ: [ 0;∞)
• Функция возрастает на промежутке [0 ;∞); функция убывает на промежутке (-∞;0 ]
• Нули функции: Y=0 при х=0
• Y наим =0 при х=0

1. ООФ: (- ∞:∞)

2. ОЗФ: ( -∞;0 ]

3. Функция возрастает на промежутке ( - ∞;0 ] ; функция убывает на промежутке [0 ;-∞ )

4. Нули функции: Y=0 при х=0

5. Y наиб =0 при х=0

0 – ветви вверх, aНаходим вершину параболы: х 0 =- b/2a , подставляем x 0 в формулу параболы и находим y 0 - (x 0 ;у 0 ) Находим точки пересечения параболы с осями координат: с Ох: у=0, решаем уравнение ах 2 + b х+с =0 и находим корни этого уравнения х 1 и х 2 – (х 1 ;0) и (х 2 ;0) с Оу: х=0, у=с – (0;с) Если необходимо находим дополнительные точки " width="640"

Построение параболы: y=ax 2 +bx+c

Парабола строится по пяти точкам

• Определить направление ветвей: a0 – ветви вверх, a
• Находим вершину параболы: х 0 =- b/2a , подставляем x 0 в формулу параболы и находим y 0 - (x 0 ;у 0 )
• Находим точки пересечения параболы с осями координат: с Ох: у=0, решаем уравнение ах 2 + b х+с =0 и находим корни этого уравнения х 1 и х 2 – (х 1 ;0) и (х 2 ;0) с Оу: х=0, у=с – (0;с)
• Если необходимо находим дополнительные точки

0) , функция отрицательна (у Наибольшее или наименьшее значение функции " width="640"

План исследование квадратичной функции

Степенная функция

• Находим ООФ – это те значения х при которых функция существует
• Находим ОЗФ – это те значения которые принимает функция (значения у)
• Промежутки возрастания и убывания функции
• Нули функции – это те х, когда у=0
• Промежутки, где функция положительна (у 0) , функция отрицательна (у
• Наибольшее или наименьшее значение функции

a ед.

Степенная функция

Кубическая – Y=x 3 и Y=-x 3

a ед.

a ед.

Гипербола у=к/х, где к – любое число, ООФ: х ≠0

Степенная функция

a ед.

a ед.

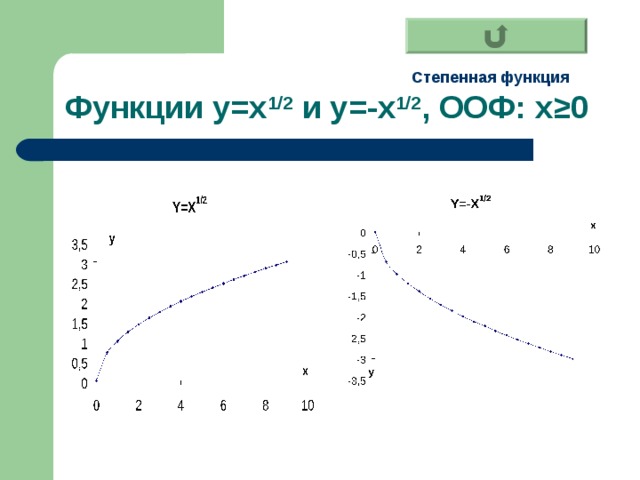
Функции y=x 1/2 и y= - x 1/2 , ООФ: х ≥0

Степенная функция

a ед.

a ед.

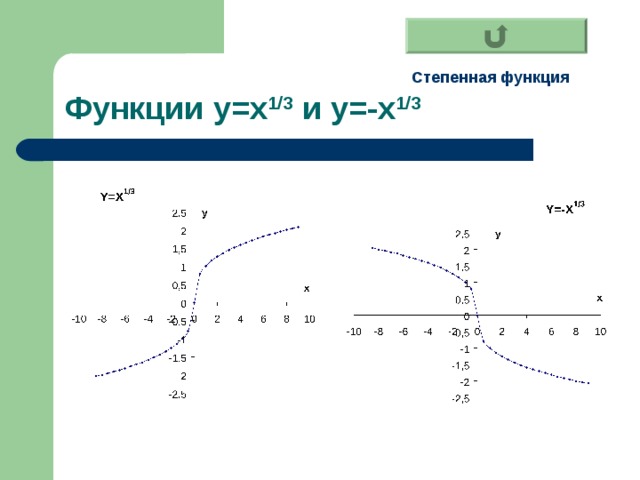
Функции y=x 1/3 и y= - x 1/3

Степенная функция

a ед.

a ед.

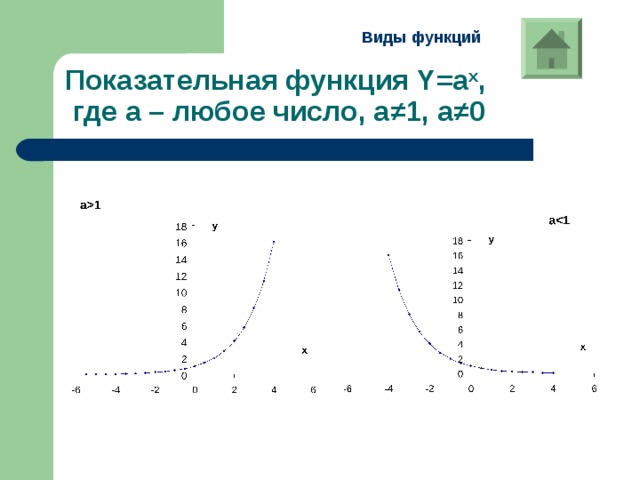
Виды функций

Показательная функция Y=a x , где а – любое число, а ≠1, а≠0

0 и а ≠1; ООФ: x0 " width="640"

a ед.

a ед.

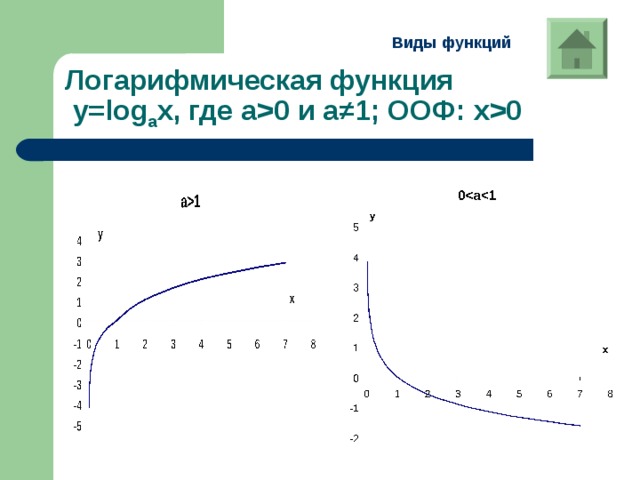
Виды функций

Логарифмическая функция y=log a x , где а 0 и а ≠1; ООФ: x0

Виды функций

Сдвиг графика в право и в лево на а единиц, где а - любое число

Виды функций

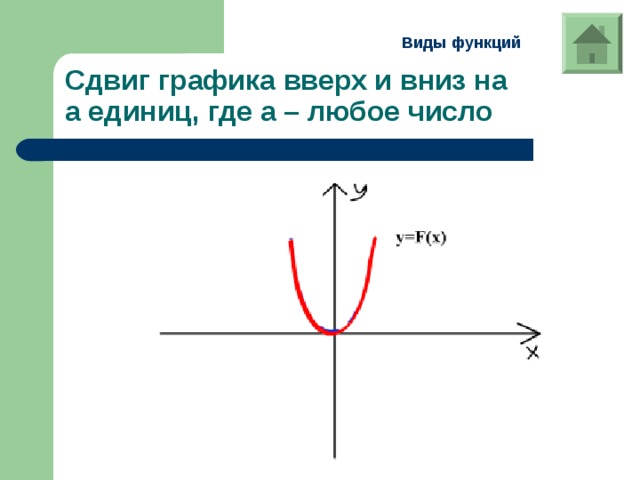
Сдвиг графика вверх и вниз на а единиц, где а – любое число

Виды функций

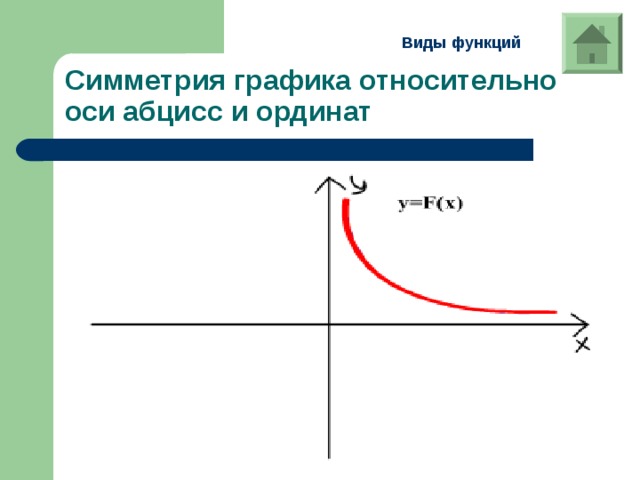
Симметрия графика относительно оси абцисс и ординат

Виды функций

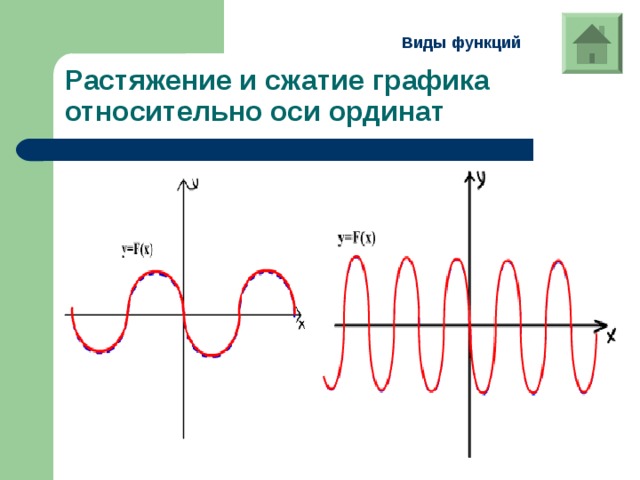
Растяжение и сжатие графика относительно оси ординат

Виды функций

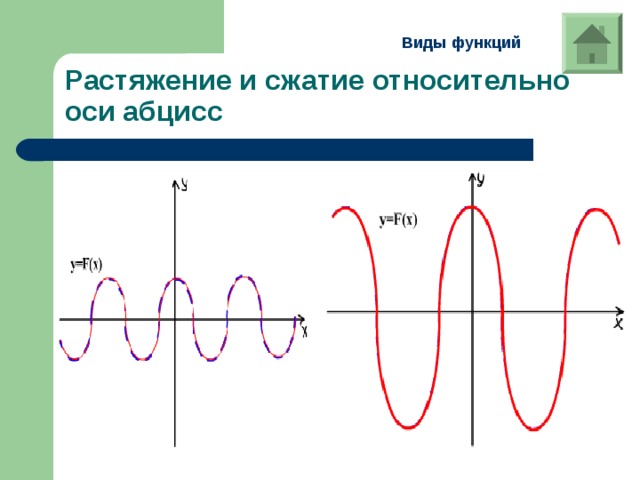
Растяжение и сжатие относительно оси абцисс