Презентация по теме "Параллелограмм" (6 класс)

Глава 12. Урок 150

ПАРАЛЛЕЛОГРАММ И ЕГО СВОЙСТВА

Далее

Устная работа.

Устная работа.

Вычислите:

а) 0,5 · 8;

е) 1,3 · 4;

б) 6 · 0,9;

ж) 6 : 1,2;

в) 1,8 : 0,3;

з) 4,5 · 0,1;

г) 247 · 0,01;

и) 3,6 : 9;

д) 1,19 : 0,1;

к) 0,8 : 0,02.

Далее

Объяснение нового материала.

– Какая фигура изображена на рисунке?

(Четырехугольник.)

– Что интересного вы замечаете в этом четырехугольнике?

(У него противоположные стороны параллельны.)

Такая фигура называется параллелограммом .

Определение.

Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны.

Далее

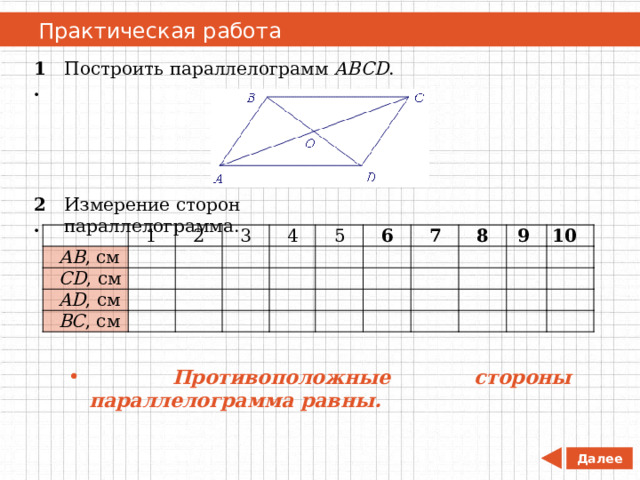
Практическая работа

1.

Построить параллелограмм ABCD .

Измерение сторон параллелограмма.

2.

АВ , см

1

2

CD , см

3

AD , см

ВС , см

4

5

6

7

8

9

10

• Противоположные стороны параллелограмма равны.

Далее

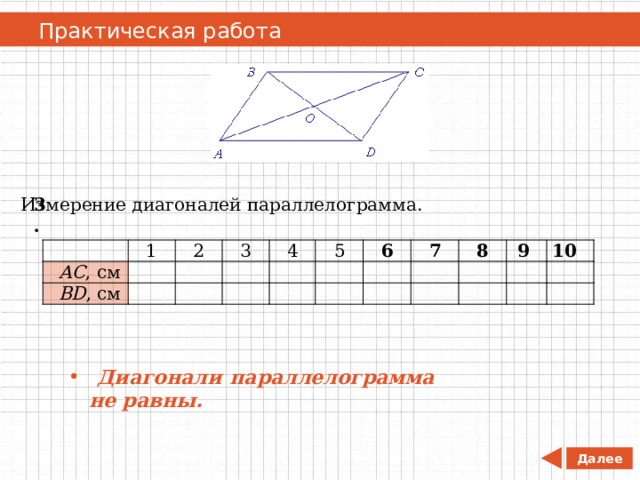
Практическая работа

3.

Измерение диагоналей параллелограмма.

АC , см

1

BD , см

2

3

4

5

6

7

8

9

10

• Диагонали параллелограмма не равны.

Далее

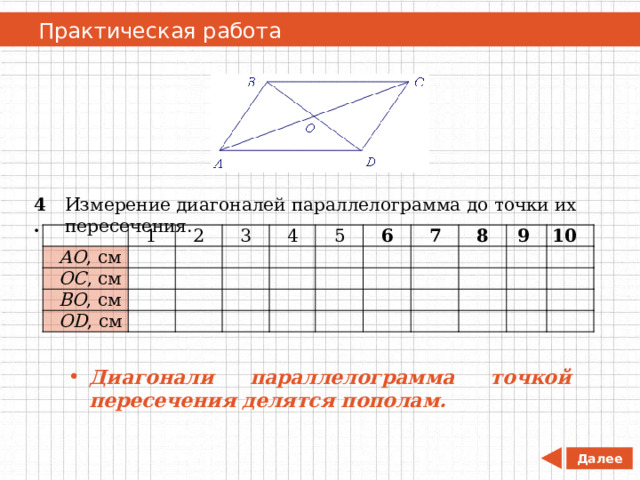
Практическая работа

Измерение диагоналей параллелограмма до точки их пересечения.

4.

АO , см

1

OC , см

2

BO , см

3

OD , см

4

5

6

7

8

9

10

• Диагонали параллелограмма точкой пересечения делятся пополам.

Далее

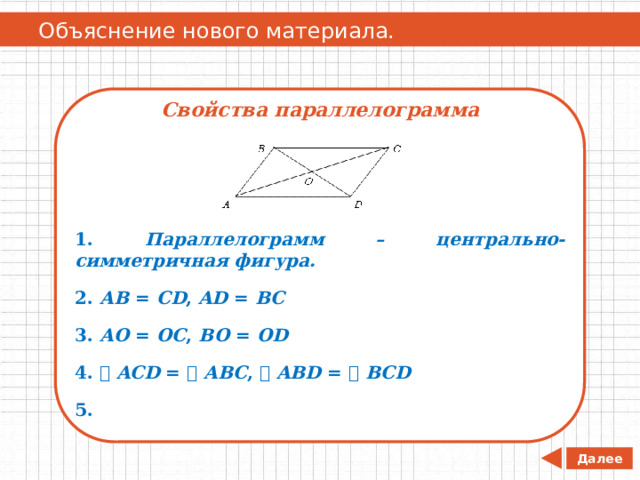
Объяснение нового материала.

Свойства параллелограмма

1. Параллелограмм – центрально-симметричная фигура.

2. АВ = СD , AD = BC

3. АO = OC , BO = OD

4.  ACD =  ABC ,  ABD =  BCD

5.

Далее

Объяснение нового материала.

Частные случаи параллелограмма.

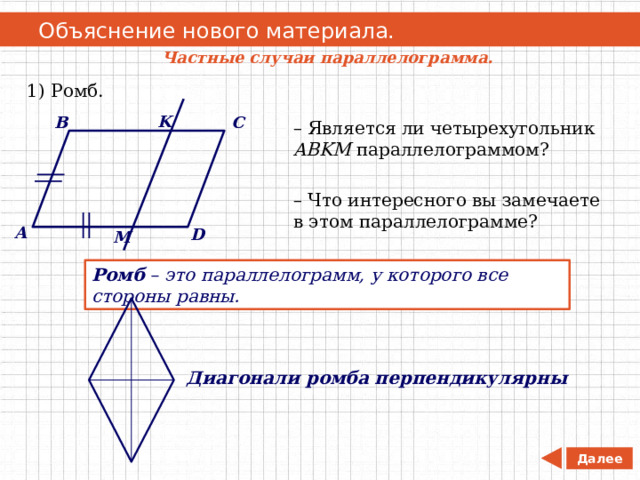
1) Ромб.

K

C

B

– Является ли четырехугольник ABKM параллелограммом?

– Что интересного вы замечаете в этом параллелограмме?

A

D

M

Ромб – это параллелограмм, у которого все стороны равны.

Диагонали ромба перпендикулярны

Далее

Объяснение нового материала.

Частные случаи параллелограмма.

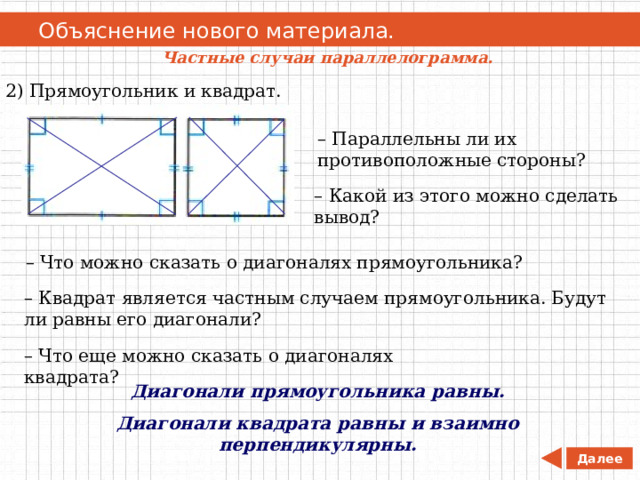
2) Прямоугольник и квадрат.

– Параллельны ли их противоположные стороны?

– Какой из этого можно сделать вывод?

– Что можно сказать о диагоналях прямоугольника?

– Квадрат является частным случаем прямоугольника. Будут ли равны его диагонали?

– Что еще можно сказать о диагоналях квадрата?

Диагонали прямоугольника равны.

Диагонали квадрата равны и взаимно перпендикулярны.

Далее

Формирование умений и навыков.

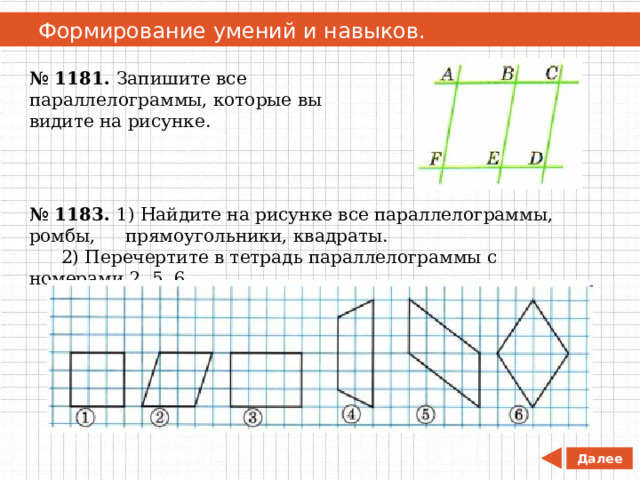
№ 1181. Запишите все параллелограммы, которые вы видите на рисунке.

№ 1183. 1) Найдите на рисунке все параллелограммы, ромбы, прямоугольники, квадраты.

2) Перечертите в тетрадь параллелограммы с номерами 2, 5, 6.

Далее

Формирование умений и навыков.

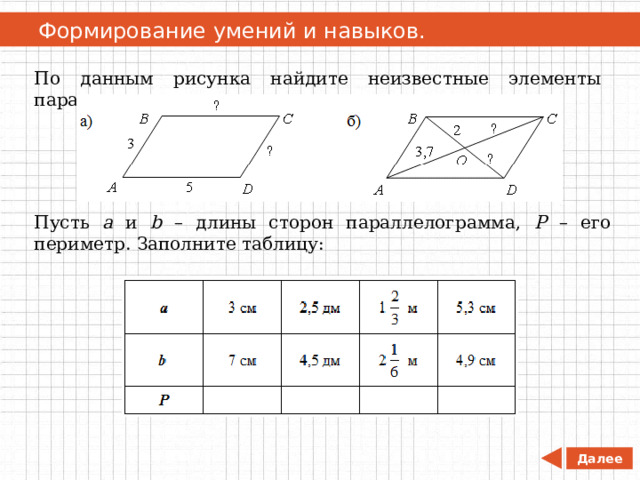
По данным рисунка найдите неизвестные элементы параллелограмма.

Пусть а и b – длины сторон параллелограмма, Р – его периметр. Заполните таблицу:

Далее

Формирование умений и навыков.

№ 1187. Обозначьте длины сторон параллелограмма буквами и составьте формулу для вычисления периметра параллелограмма. Составьте формулу для вычисления периметра ромба.

Периметр параллелограмма равен 28 см, а одна из его сторон равна 6 см. Найдите остальные стороны параллелограмма.

Далее

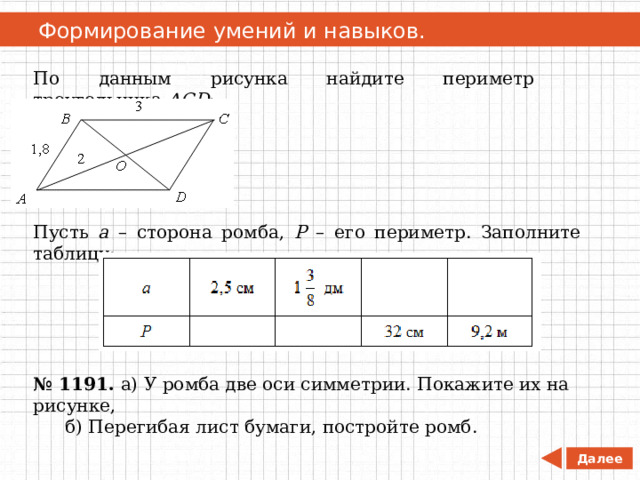
Формирование умений и навыков.

По данным рисунка найдите периметр треугольника АСD :

Пусть а – сторона ромба, Р – его периметр. Заполните таблицу:

№ 1191. а) У ромба две оси симметрии. Покажите их на рисунке,

б) Перегибая лист бумаги, постройте ромб.

Далее

Итоги урока.

– Какая фигура называется параллелограммом?

– Перечислите основные свойства параллелограмма.

– Что такое ромб?

– Какое у ромба есть отличительное свойство?

– Какими свойствами обладают диагонали прямоугольника и квадрата?

– Назовите формулу, по которой можно вычислить периметр параллелограмма; ромба.

Домашнее задание.

№ 1184; 1186; 1188.

Далее