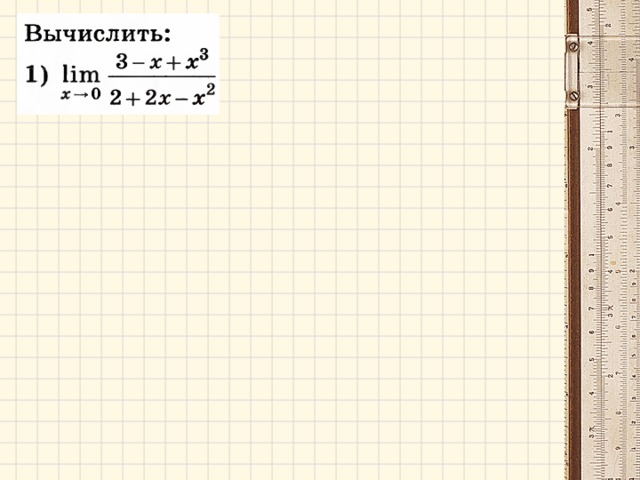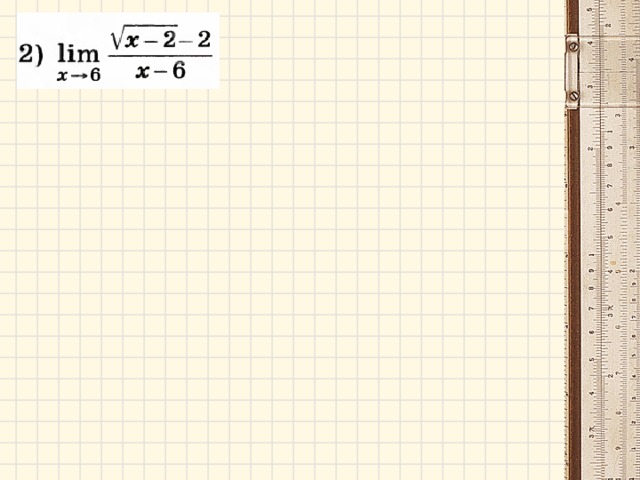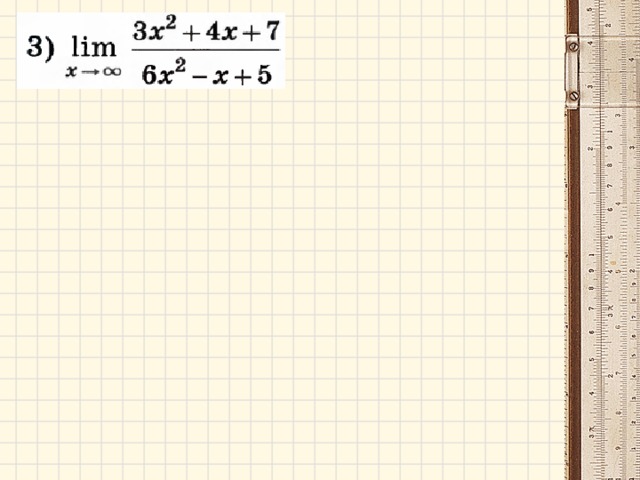19.12.19
Предел последовательности
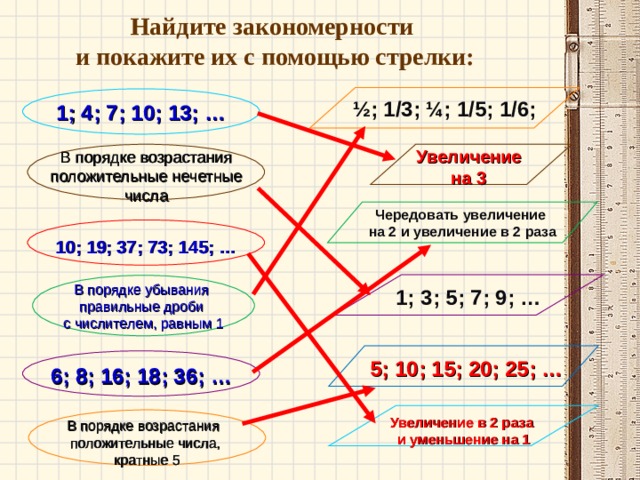
Найдите закономерности и покажите их с помощью стрелки:
½; 1/3; ¼; 1/5; 1/6;
1; 4; 7; 10; 13; …
Увеличение
на 3
В порядке возрастания
положительные нечетные
числа
Чередовать увеличение
на 2 и увеличение в 2 раза
10; 19; 37; 73; 145; …
1; 3; 5; 7; 9; …
В порядке убывания
правильные дроби
с числителем, равным 1
5; 10; 15; 20; 25; …
6; 8; 16; 18; 36; …
Увеличение в 2 раза
и уменьшение на 1
В порядке возрастания
положительные числа,
кратные 5

Что такое числовая последовательность?
- Если каждому натуральному числу п поставлено в соответствие некоторое действительное число х п , то говорят,
что задана числовая последовательность .
Числовая последовательность – это функция ,
область определения которой есть множество N
всех натуральных чисел. Множество значений этой функции – совокупность чисел х п , п ϵ Ν , называют множеством значений последовательности.
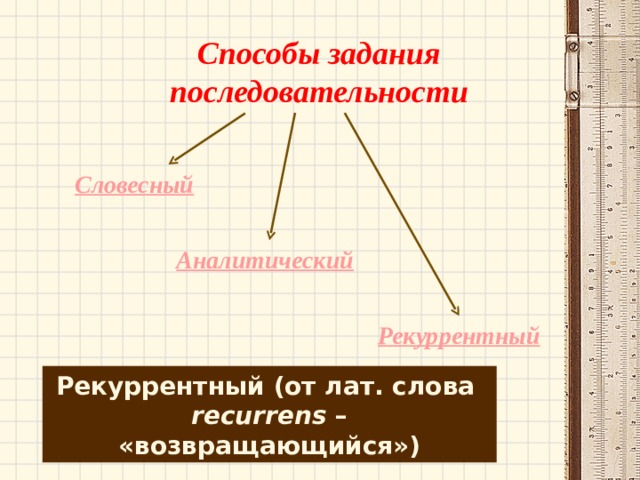
Способы задания последовательности
Словесный
Аналитический
Рекуррентный
Рекуррентный (от лат. слова
recurrens – «возвращающийся»)

Словесный способ.
Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.
- Пример 1. Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .
- Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, ... .
- Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, ... .

Аналитический способ .
- Пример 1. Последовательность чётных чисел: y = 2 n ;
- 2, 4, 6, 8, …, 2п,… .
- Пример 2. Последовательность квадрата натуральных чисел: y = n 2 ;
- 1, 4, 9, 16, 25, ..., n 2 , ... .
- Пример 3. Последовательность y = 2 n ;
- 2, 22, 23, 24, ..., 2 n , ... .

Рекуррентный способ.
- Указывается правило, позволяющее вычислить n -й элемент последовательности, если известны её предыдущие элементы.
- Пример 1. a 1 = a , an +1= an + d , где a и d – заданные числа. Пусть a 1 =5, d =0,7, тогда последовательность будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; ... .
- Пример 2. b 1 = b , b n +1 = bn q , где b и q – заданные числа. Пусть b 1 =23, q =½, тогда последовательность будет иметь вид: 23; 11,5; 5,75; 2,875; ... .

Предел числовой последовательности
Рассмотрим две числовые последовательности:
: 2, 4, 6, 8, 10, …, 2п ,…;
: 1, , , , , … , …
Изобразим члены этих последовательностей точками на координатных прямых.
Обратите внимание как ведут себя члены
последовательности.

Замечаем, что члены последовательности у п как бы «сгущаются» около точки 0, а у последовательности х п таковой точки не наблюдается.
Но, естественно, не всегда удобно изображать члены последовательности, чтобы узнать есть ли точка «сгущения» или нет, поэтому математики придумали следующее…

Определение 1.
Пусть a - точка прямой, а r положительное число. Интервал (a-r, a+r) называют окрестностью точки a ,
а число r радиусом окрестности .
Геометрически это выглядит так:

Например
(-0.1, 0.5) – окрестность точки 0.2, радиус окрестности равен 0. 3.
Теперь можно перейти к определению точки
«сгущения», которую математики назвали
« пределом последовательности ».

Число b называется пределом последовательности { у п } если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера.
Пишут: .
Читают:
стремится к .
Либо пишут: .
Читают: предел последовательности у п при
стремлении п к бесконечности равен b .

Последовательность, имеющая предел, называется сходящейся ; в противном случае – расходящейся .
 1 , то последовательность у n = q n расходится " width="640"
1 , то последовательность у n = q n расходится " width="640"
Рассмотрим последовательность :
– гармонический ряд
Если m N, k R, то
Если │ q │ , то
Если │ q │ 1 , то последовательность у n = q n
расходится

Свойства пределов
Если , ,
- предел суммы равен сумме пределов:
- предел произведения равен произведению пределов:
- предел частного равен частному пределов:
- постоянный множитель можно вынести за знак
предела:

Примеры:
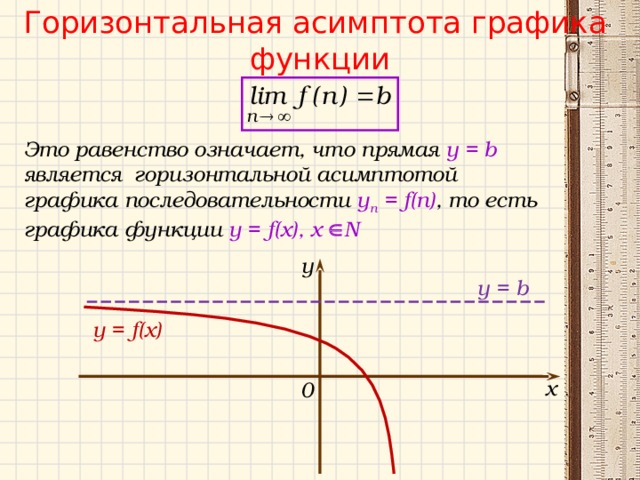
Горизонтальная асимптота графика
функции
Это равенство означает, что прямая у = b является горизонтальной асимптотой графика последовательности y n = f(n) , то есть графика функции y = f( х ) , х N
у
у = b
y = f(x)
х
0
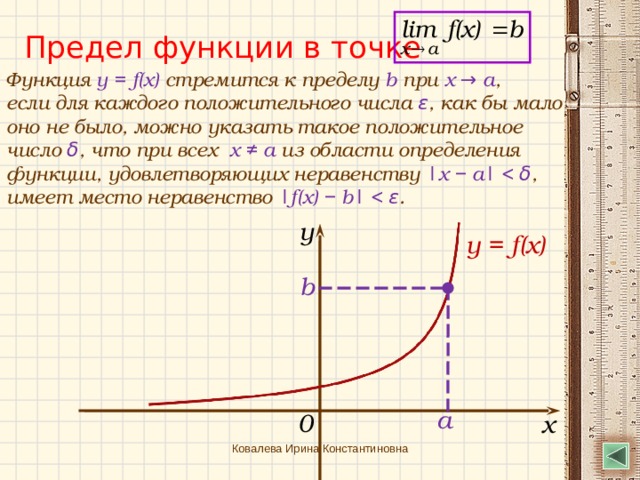
Предел функции в точке
Функция y = f(x) стремится к пределу b при x → a ,
если для каждого положительного числа ε , как бы мало оно не было, можно указать такое положительное число δ , что при всех x ≠ a из области определения функции, удовлетворяющих неравенству |x − a| ,
имеет место неравенство |f(x) − b| .
у
y = f(x)
b
а
0
х
Ковалева Ирина Константиновна

Непрерывность функции в точке
Функцию y = f(x) называют непрерывной в точке
x = a , если выполняется условие
Примеры:

Понятие непрерывности функции
На рисунке изображен график функции, состоящий из двух «кусков». Каждый из них может быть нарисован без отрыва от бумаги. Однако эти «куски» не соединены непрерывно в точке х =1.
Поэтому все значения х, кроме х =1, называют точками непрерывности функции у = f (х), а точку х =1 – точкой разрыва этой функции.
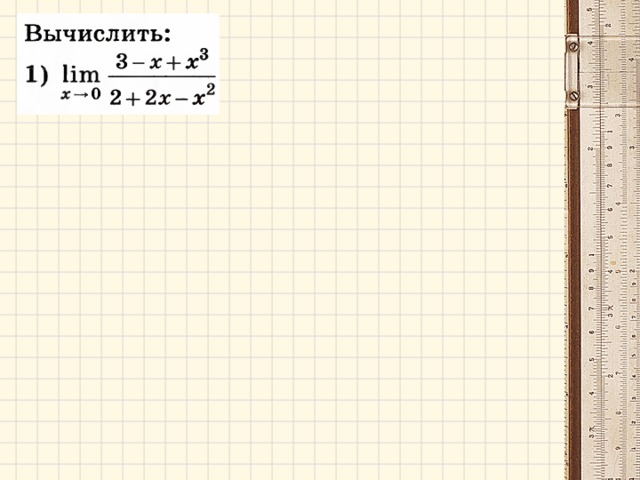
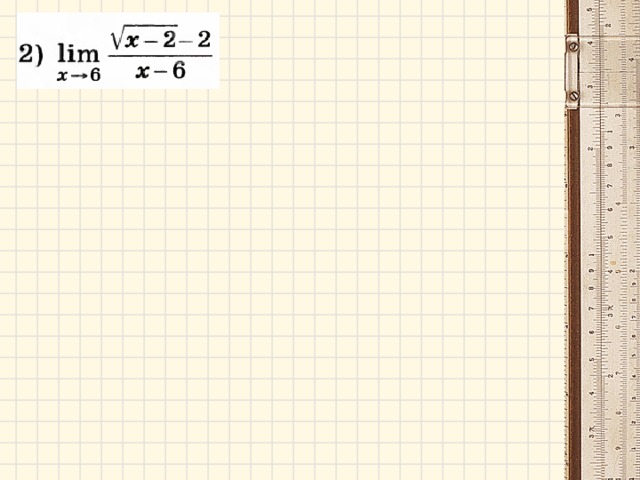
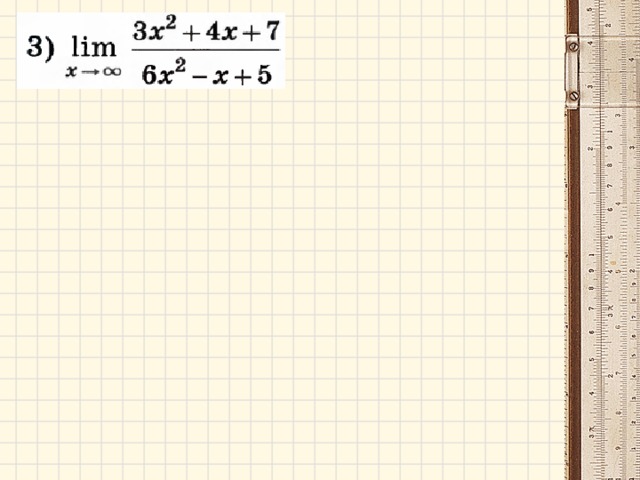





















 1 , то последовательность у n = q n расходится " width="640"
1 , то последовательность у n = q n расходится " width="640"