Презентация "Признаки параллельности двух прямых"

7 класс, геометрия

10.01.2023 Признаки параллельности двух прямых

7 класс, геометрия. Признаки параллельности двух прямых

Цель:

• повторить определение параллельных прямых, смежных и вертикальных углов;
• формировать понятие накрест лежащих, односторонних и соответственных углов;
• рассмотреть признаки параллельности прямых и первичное применение их при решении задач.

Тип урока: изучение нового материала

Ход урока: Изучить презентацию, разобрать решение задач.

Параллельные прямые

Определение

Две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные прямые имеют своё обозначение: a ║ b.

Параллельность двух лучей, отрезка и прямой, луча и прямой, луча и отрезка определяется аналогично.

Например, отрезок PQ параллелен прямой  n :

Отрезок ST параллелен лучу EF:

• Рассмотрим прямую с, пересекающую прямые а и b.
• Прямая  c  называется секущей по отношению к прямым  a  и  b , если она пересекает каждую из них (пересекает их в двух точках).
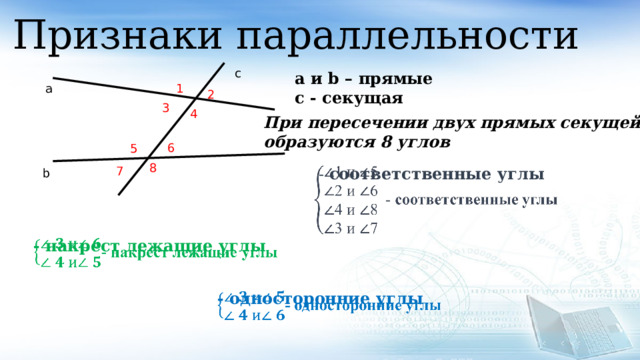
• Как видно из рисунка, при пересечении прямых а и b секущей c образуются 8 углов. Пронумеруем полученные углы.
• Некоторые пары образованных углов имеют свои названия.

• накрест лежащие углы: углы 3 и 5, 4 и 6.
• односторонние углы: углы 4 и 5 или 3 и 6.
• соответственные углы: углы 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Рассмотрим три признака параллельности двух прямых

Признаки параллельности

c

a и b – прямые

с - секущая

a

1

2

3

4

При пересечении двух прямых секущей

образуются 8 углов

6

5

8

7

- соответственные углы

b

- накрест лежащие углы

- односторонние углы

Признаки параллельности

c

c

Если накрест лежащие углы,

образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны

3

4

a

a

3

4

6

5

6

5

b

b

3 = 6

4 = 5

прямые параллельны

Теорема 1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые  a  и  b,  секущая  AB, ∠ 1 = ∠ 2 накрест лежащие.

Доказать:  a║b.

Доказательство:

1 случай:

∠ 1 = ∠2 = 90°

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠  1= ∠ 2 ≠ 90°

1) Из середины O отрезка  AB  проведём перпендикуляр OH к прямой  а.  На прямой  b  от точки B отложим отрезок BH 1 , равный отрезку AH и проведем отрезок OH 1 .

2) AO = OB т. к. O середина  AB ; AH = BH 1  по построению; ∠1 = ∠2 по условию.

Тогда ΔOHA = ΔOH 1 B по первому признаку равенства треугольников.

Далее из равенства треугольников следует равенство углов: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H 1  лежит на продолжении луча OH. Это значит, что точки H 1 , O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a   и  b  перпендикулярны к третьей НН 1 , а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Практическое задание №1

Будут ли прямые a и b параллельны, если:

c

3

4

a

нет

1) 3 = 86° и 6 = 87°

6

5

2) 4 = 119° и 5 = 119°

да

b

нет

3) 4 = 138° и 5 = 128°

да

4) 3 = 63° и 6 = 63°

Признаки параллельности

c

c

1

2

1

a

a

4

2

3

3

4

Если соответственные углы,

образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны

6

5

6

5

8

8

7

b

7

b

прямые параллельны

Теорема 2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны .

Дано: прямые  a  и  b, секущая AB, 

∠ 1 = ∠2 соответственные.

Доказать:  a ║b.

Доказательство:

∠ 1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно,  a║b  по Теореме 1.

Практическое задание №2

Будут ли прямые a и b параллельны, если:

c

1

2

a

4

3

1) 1 = 129° и 5 = 119°

нет

6

5

да

2) 4 = 163° и 8 = 163°

8

7

b

3) 2 = 65° и 6 = 75°

нет

да

4) 3 = 58° и 7= 58°

Признаки параллельности

c

c

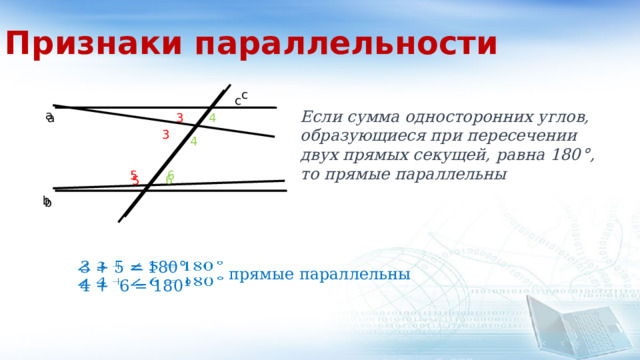
Если сумма односторонних углов,

образующиеся при пересечении двух прямых секущей, равна 180 ° , то прямые параллельны

a

4

3

a

3

4

6

5

6

5

b

b

3 + 5 = 180 °

4 + 6 = 180 °

прямые параллельны

Теорема 3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Дано:

Прямые  a  и  b, секущая AB,  ∠1 + ∠2 = 180° ‑ односторонние.

Доказать:  a║b.

Доказательство

∠ 3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠ 1 + ∠2 = 180 °  по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно,  a║b  по теореме 1.

Практическое задание №3

Будут ли прямые a и b параллельны, если:

c

4

a

3

нет

1) 3 = 25° и 5 = 125°

2) 4 = 147° и 6 = 33°

да

6

5

нет

3) 4 = 124° и 6 = 36°

b

да

4) 3 = 72° и 5 = 108°

Задача №1

Дано: ∠1= 60°, ∠2 = 120°.

Докажите:  a║b

Решение:

∠ 2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;

∠ 3 = ∠1, это накрест лежащие углы;

Значит, прямые  a и b  параллельны по 1 признаку параллельности прямых.

Ответ: прямые  a и b  параллельны по 1 признаку параллельности прямых.

Задача №2

Дано: ΔABC – равнобедренный,

∠ А = 60°. CD – биссектриса ∠BCK.

Докажите: AB ║ CD.

Доказательство:

∠ A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.

∠ BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.

∠ BCD = ∠DСK = 60° т. к. CD – биссектриса делит угол ∠BCK пополам.

Значит, ∠A = ∠DCK = 60° ‑ соответственные при пересечении прямых АВ и СD секущей АК. Следовательно, AB║CD по 2 признаку параллельности прямых.

Ответ: AB║CD по 2 признаку параллельности прямых.

Задача №3

Один из односторонних углов при двух параллельных прямых и секущей на 40  меньше другого. Найдите меньший угол.

Решение:

Пусть х – меньший из односторонних углов, тогда больший равен х + 40. Т. к. прямые параллельны, то сумма односторонних углов равна 180°, составим уравнение.

х + х + 40 = 180

2х + 40 = 180

2х = 180 – 40

х = 140:2

х = 70° – градусная мера меньшего угла.

Ответ: 70°.

Задача №4

По данным рисунка докажите, что АВ  DE

Задача №5

Подставьте названия углов к соответствующим изображениям.

Задача №6

Отметьте, на каких рисунках представлены пары параллельных прямых

Задача №7

Посмотрите на рисунок. Подчеркните верное утверждение.

Задание №8

Установите параллельны прямые или нет тремя различными способами

1

2

3

Задача №9

В четырёхугольнике ABCD все стороны равны. Укажите, из равенства каких углов можно сделать вывод о параллельности его сторон.

CAD

AD

CD

DCA

Практическое задание №4

Будут ли прямые a и b параллельны, если:

c

3

4

a

нет

1) 3 = 86° и 6 = 87°

да

6

5

2) 4 = 119° и 5 = 119°

b

нет

3) 4 = 138° и 5 = 128°

4) 3 = 63° и 6 = 63°

да

Домашнее задание:

Выучить формулировку и доказательство теорем: § 1, п.24, 25

Выполнить: № 186, №189 стр. 56

Успешного выполнения домашнего задания!