
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ШКОЛА № 1 Г.О. ЕНАКИЕВО» Тема урока: «Возрастание и убывание функции» 11 класс Учитель математики Фоменко Н.Г.

Немного повторения
- Понятия возрастающей и убывающей функций.
- Понятие монотонности функции.
 х 1 следует неравенство f(х 2 ) f(х 1 ). х 1 х 2 х f (х 1 ) " width="640"
х 1 следует неравенство f(х 2 ) f(х 1 ). х 1 х 2 х f (х 1 ) " width="640"
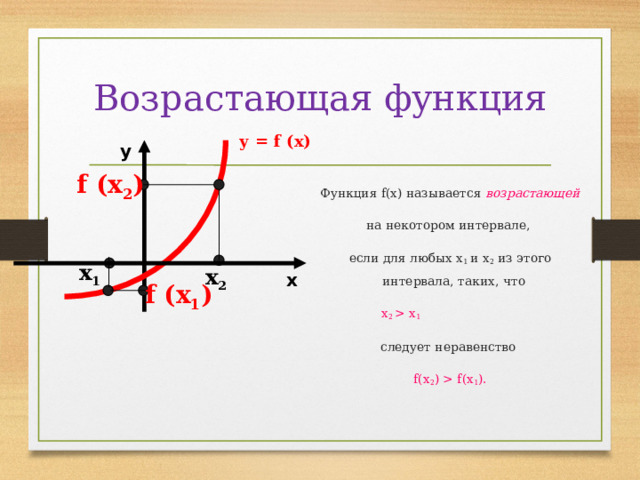
Возрастающая функция
у = f (х)
у
f (х 2 )
Функция f(х) называется возрастающей
на некотором интервале,
если для любых х 1 и х 2 из этого интервала, таких, что
х 2 х 1
следует неравенство
f(х 2 ) f(х 1 ).
х 1
х 2
х
f (х 1 )
 х 1 следует неравенство f(х 2 ) f(х 1 ). f (х 1 ) х 1 х 2 х " width="640"
х 1 следует неравенство f(х 2 ) f(х 1 ). f (х 1 ) х 1 х 2 х " width="640"
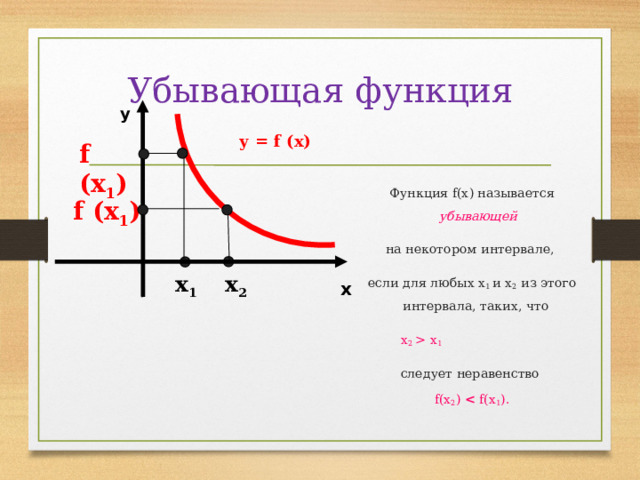
Убывающая функция
у
у = f (х)
f (х 1 )
Функция f(х) называется убывающей
на некотором интервале,
если для любых х 1 и х 2 из этого интервала, таких, что
х 2 х 1
следует неравенство
f(х 2 ) f(х 1 ).
f (х 1 )
х 1
х 2
х
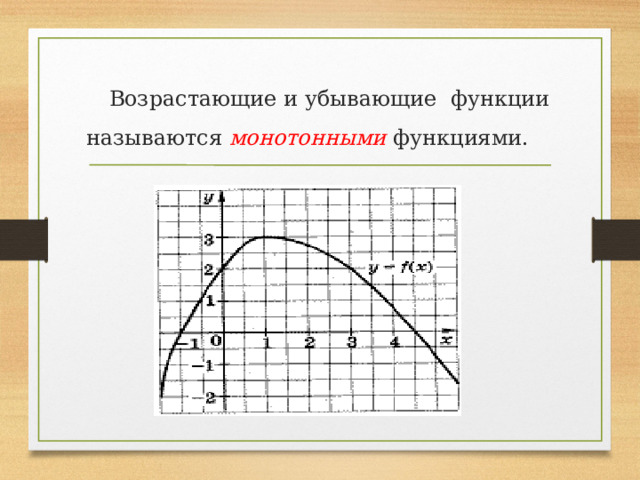
Возрастающие и убывающие функции называются монотонными функциями.

Способы исследования функций на монотонность
Способ 1. По определению возрастающей (убывающей) функции.
Способ 2. По графику функции.
 x 1 , тогда f(x 2 ) - f(x 1 ) = 1/ x 2 – 1/ x 1 = ( х 1 –х 2 )/ х 2 х 1 , значит данная функция убывает на каждом из двух промежутков своей области определения. " width="640"
x 1 , тогда f(x 2 ) - f(x 1 ) = 1/ x 2 – 1/ x 1 = ( х 1 –х 2 )/ х 2 х 1 , значит данная функция убывает на каждом из двух промежутков своей области определения. " width="640"
Пример №1. Исследуйте функцию f(x)= 1/х на
монотонность.
Решение.
D(f) : х ≠ 0
Пусть х 2 и x 1 - произвольные точки из D(f) такие, что х 2 x 1 , тогда f(x 2 ) - f(x 1 ) = 1/ x 2 – 1/ x 1 = ( х 1 –х 2 )/ х 2 х 1 , значит данная функция убывает на каждом из двух промежутков своей области определения.
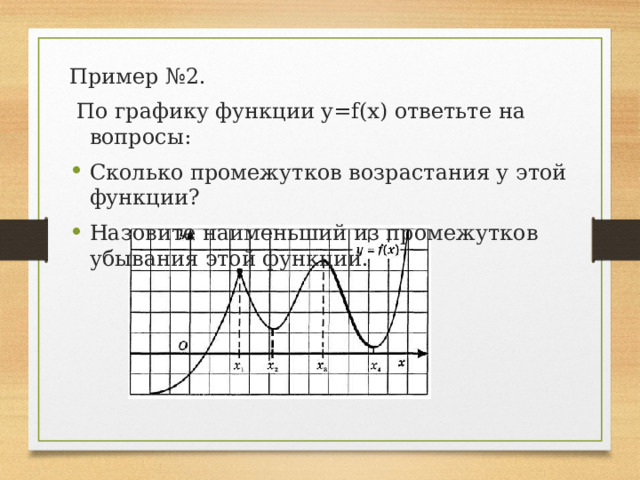
Пример №2.
По графику функции y=f(x) ответьте на вопросы:
- Сколько промежутков возрастания у этой функции?
- Назовите наименьший из промежутков убывания этой функции.
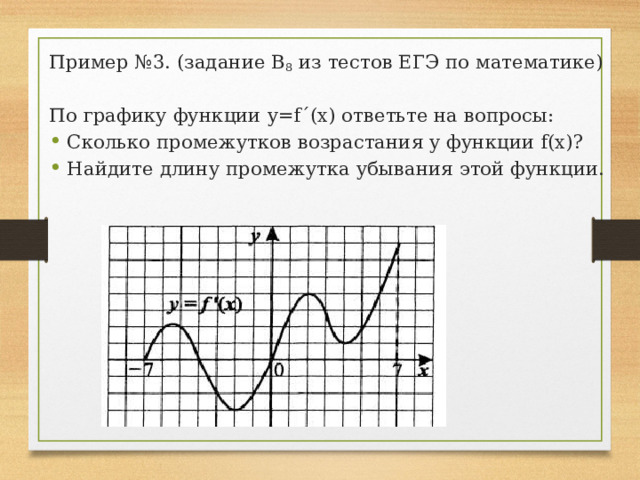
Пример №3. (задание В 8 из тестов ЕГЭ по математике)
По графику функции y=f´(x) ответьте на вопросы:
- Сколько промежутков возрастания у функции f(x)?
- Найдите длину промежутка убывания этой функции.

Наши цели
1. Найти связь между производной и свойством монотонности функции.
2. Создать алгоритм поиска промежутков монотонности функции с помощью производной.
 0 на некотором интервале, то функция возрастает на этом интервале. Если f / (x) " width="640"
0 на некотором интервале, то функция возрастает на этом интервале. Если f / (x) " width="640"
Гипотеза
- Если f / (x) 0 на некотором интервале, то функция возрастает на этом интервале.
- Если f / (x)

Достаточный признак возрастания(убывания) функции
 0 (график расположен выше оси Х) 3.2. f ’(x) 4. Определить промежутки монотонности. 4.1. Если f ’(x) 0 , то функция возрастает на данном промежутке. 4.2. Если f ’(x) " width="640"
0 (график расположен выше оси Х) 3.2. f ’(x) 4. Определить промежутки монотонности. 4.1. Если f ’(x) 0 , то функция возрастает на данном промежутке. 4.2. Если f ’(x) " width="640"
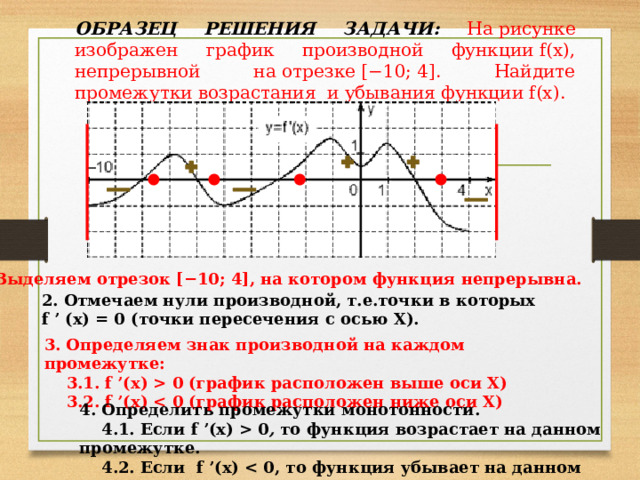
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ: На рисунке изображен график производной функции f(x), непрерывной на отрезке [−10; 4]. Найдите промежутки возрастания и убывания функции f(x).
1. Выделяем отрезок [−10; 4], на котором функция непрерывна.
2. Отмечаем нули производной, т.е.точки в которых f ’ (x) = 0 (точки пересечения с осью Х).
3. Определяем знак производной на каждом промежутке:
3.1. f ’(x) 0 (график расположен выше оси Х)
3.2. f ’(x)
4. Определить промежутки монотонности.
4.1. Если f ’(x) 0 , то функция возрастает на данном промежутке.
4.2. Если f ’(x)
![РЕШАЕМ ВМЕСТЕ ЗАДАЧУ: На рисунке изображен график производной функции f(x), непрерывной на отрезке [−4; 6]. Найдите промежутки возрастания и убывания функции f(x). Функция у = f(х) убывает при х є [-4;-2) ; (2; 6] Функция у = f(х) возрастает при х є (-2;2)](https://fsd.multiurok.ru/html/2025/01/31/s_679d3371b235c/img14.jpg)
РЕШАЕМ ВМЕСТЕ ЗАДАЧУ: На рисунке изображен график производной функции f(x), непрерывной на отрезке [−4; 6]. Найдите промежутки возрастания и убывания функции f(x).
Функция у = f(х) убывает при х є [-4;-2) ; (2; 6]
Функция у = f(х) возрастает при х є (-2;2)
![№ 1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.](https://fsd.multiurok.ru/html/2025/01/31/s_679d3371b235c/img15.jpg)
№ 1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.
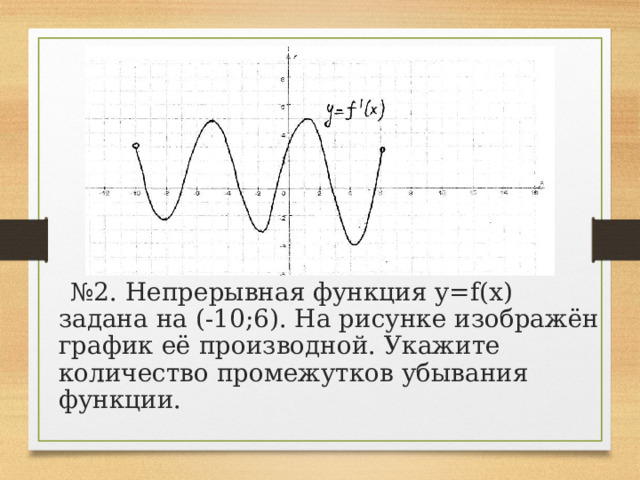
№ 2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество промежутков убывания функции.
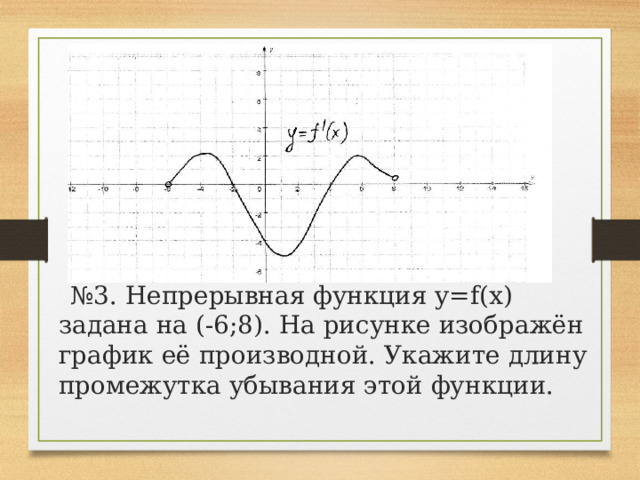
№ 3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её производной. Укажите длину промежутка убывания этой функции.
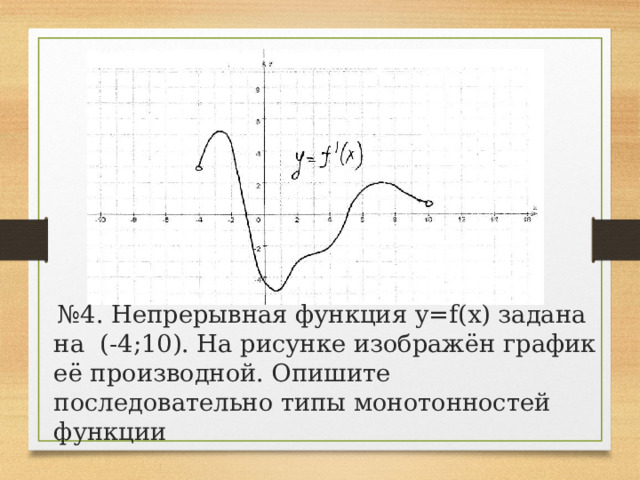
№ 4. Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её производной. Опишите последовательно типы монотонностей функции
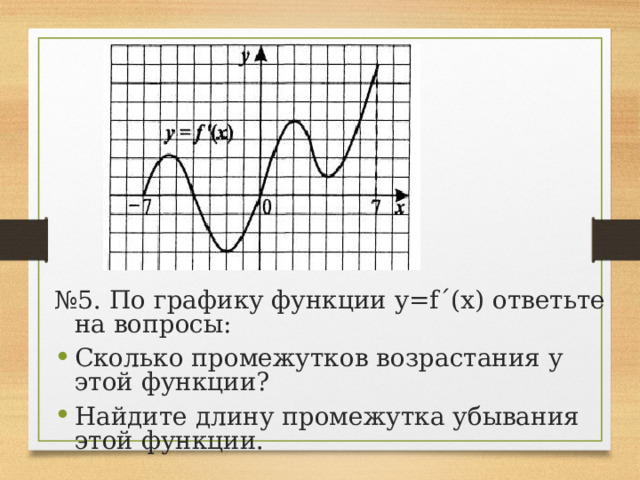
№ 5. По графику функции y=f´(x) ответьте на вопросы:
- Сколько промежутков возрастания у этой функции?
- Найдите длину промежутка убывания этой функции.
 0 и f / (x) 4. Сделать выводы о монотонности функции. " width="640"
0 и f / (x) 4. Сделать выводы о монотонности функции. " width="640"
Алгоритм
1. Указать область определения функции.
2. Найти производную функции.
3. Определить промежутки, в которых
f / (x) 0 и f / (x)
4. Сделать выводы о монотонности
функции.
 0, если 4х 3 - 4х 0, х 3 - х 0, х(х-1)(х+1)0 f / (x): - + - + -1 0 1 х f(х): 4. Функция убывает на промежутках (-∞;-1) ] и [ (0; 1) ] . Функция возрастает на промежутках [ (-1; 0) ] и [ (1; + ∞) ] " width="640"
0, если 4х 3 - 4х 0, х 3 - х 0, х(х-1)(х+1)0 f / (x): - + - + -1 0 1 х f(х): 4. Функция убывает на промежутках (-∞;-1) ] и [ (0; 1) ] . Функция возрастает на промежутках [ (-1; 0) ] и [ (1; + ∞) ] " width="640"
Образец решения по алгоритму
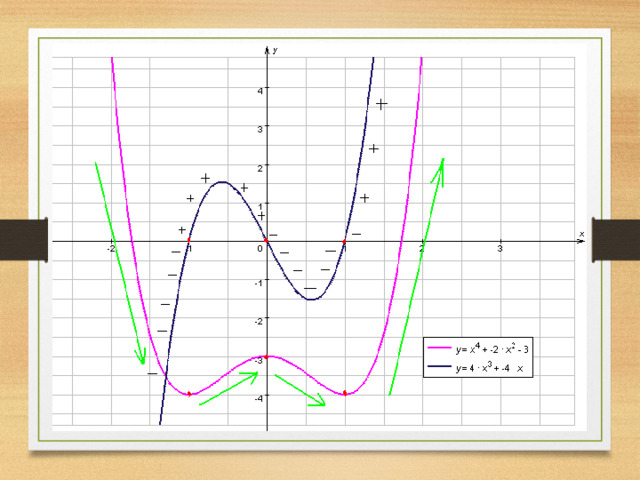
f(х) = х 4 - 2х 2 ,
1. D(f) = R
2. f / (x) = 4х 3 - 4х,
3. f / (x)0, если 4х 3 - 4х 0, х 3 - х 0, х(х-1)(х+1)0
f / (x): - + - +
-1 0 1 х
f(х):
4. Функция убывает на промежутках (-∞;-1) ] и [ (0; 1) ] .
Функция возрастает на промежутках [ (-1; 0) ] и [ (1; + ∞) ]

Домашнее задание:
- §49, стр. 257 (Выучить формулировки теорем и алгоритм исследования функции на монотонность) ,
Решать: №№ 900(1,2,4), 902(3), 903(2),956(1,4).
Дополнительно: №№ 904,905.








 х 1 следует неравенство f(х 2 ) f(х 1 ). х 1 х 2 х f (х 1 ) " width="640"
х 1 следует неравенство f(х 2 ) f(х 1 ). х 1 х 2 х f (х 1 ) " width="640"
 х 1 следует неравенство f(х 2 ) f(х 1 ). f (х 1 ) х 1 х 2 х " width="640"
х 1 следует неравенство f(х 2 ) f(х 1 ). f (х 1 ) х 1 х 2 х " width="640"


 x 1 , тогда f(x 2 ) - f(x 1 ) = 1/ x 2 – 1/ x 1 = ( х 1 –х 2 )/ х 2 х 1 , значит данная функция убывает на каждом из двух промежутков своей области определения. " width="640"
x 1 , тогда f(x 2 ) - f(x 1 ) = 1/ x 2 – 1/ x 1 = ( х 1 –х 2 )/ х 2 х 1 , значит данная функция убывает на каждом из двух промежутков своей области определения. " width="640"




 0 на некотором интервале, то функция возрастает на этом интервале. Если f / (x) " width="640"
0 на некотором интервале, то функция возрастает на этом интервале. Если f / (x) " width="640"

 0 (график расположен выше оси Х) 3.2. f ’(x) 4. Определить промежутки монотонности. 4.1. Если f ’(x) 0 , то функция возрастает на данном промежутке. 4.2. Если f ’(x) " width="640"
0 (график расположен выше оси Х) 3.2. f ’(x) 4. Определить промежутки монотонности. 4.1. Если f ’(x) 0 , то функция возрастает на данном промежутке. 4.2. Если f ’(x) " width="640"
![РЕШАЕМ ВМЕСТЕ ЗАДАЧУ: На рисунке изображен график производной функции f(x), непрерывной на отрезке [−4; 6]. Найдите промежутки возрастания и убывания функции f(x). Функция у = f(х) убывает при х є [-4;-2) ; (2; 6] Функция у = f(х) возрастает при х є (-2;2)](https://fsd.multiurok.ru/html/2025/01/31/s_679d3371b235c/img14.jpg)
![№ 1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.](https://fsd.multiurok.ru/html/2025/01/31/s_679d3371b235c/img15.jpg)




 0 и f / (x) 4. Сделать выводы о монотонности функции. " width="640"
0 и f / (x) 4. Сделать выводы о монотонности функции. " width="640"
 0, если 4х 3 - 4х 0, х 3 - х 0, х(х-1)(х+1)0 f / (x): - + - + -1 0 1 х f(х): 4. Функция убывает на промежутках (-∞;-1) ] и [ (0; 1) ] . Функция возрастает на промежутках [ (-1; 0) ] и [ (1; + ∞) ] " width="640"
0, если 4х 3 - 4х 0, х 3 - х 0, х(х-1)(х+1)0 f / (x): - + - + -1 0 1 х f(х): 4. Функция убывает на промежутках (-∞;-1) ] и [ (0; 1) ] . Функция возрастает на промежутках [ (-1; 0) ] и [ (1; + ∞) ] " width="640"











