Презентация. Замечательные точки треугольника

Проект

Замечательные точки треугольника

Учитель математики

МКОУ Данильская ООШ

Павловского района

Бабенко С. Я.

Историческая справка

  С одной стороны, история математики – это непрерывный процесс открытий; с другой стороны, открытия в математике, касающиеся геометрии треугольника, были сделаны по преимуществу в Античный период, в период позднего Средневековья и начала Нового времени. Поэтому здесь рассмотрим развитие математики в эти периоды. Свойства треугольника были хорошо изучены еще в древности греками. В знаменитых «Началах» Евклида доказывается, что центром окружности, описанном около треугольника, является точка пересечения серединных перпендикуляров к его сторонам. Архимед, определяя положение центра тяжести треугольной пластинки, установил, что он лежит на каждой из трех медиан. Известно, что в «Началах» Евклида излагается материал о центрах вписанной и описанной окружностей, точек пересечения медиан, высот и биссектрис. Есть основания полагать, что греки до Евклида обладали этими знаниями, а Евклид их просто систематизировал и включил в «Начала» для полноты изложения материала. Принято считать, что вся современная наука оформилась в 17 веке. Начало открытий замечательных точек треугольника, не изучаемых в школе, положил в 17 веке Джованни Чева (Ceva) (1648 - 1734) – итальянский математик. Основной заслугой Чевы является построение учения о секущих, которое положило начало новой – синтетической геометрии; оно изложено в сочинении "О взаимнопересекающихся прямых" (De lineis rectis se inuicem secantibus statica constructio, Mediolani, 1678). Во-первых, его теорема (знаменитая теорема Чевы) сама по себе представляет ценность, во-вторых, ее применение позволило открыть свойства замечательных точек треугольника, известных как точки Нагеля и Жергонна.

Следующим продвижением в истории математики является доказательство Готфридом Лейбницем теоремы о пересечении медиан в 1701 году в Берлине. Воспользовавшись этим результатом, Эйлер в докладе Российской Академии наук изложил факт, известный ныне как свойство прямой Эйлера. В 19 веке появляется публикация молодого французского математика Ферма расчетов, связанных с минимальным суммарным расстоянием до вершин треугольника. Уже в конце 19 века Брокар, Нагель и Торричелли, изучая труды Ферма и применяя теорему Чевы, замечают неопубликованные ранее никем некоторые свойства точки Ферма. Примерно в это же время – вторая половина 19 века – итальянский математик Наполеон Фьеорованти применяет оригинальную идею: по аналогии с «Пифагоровыми штанами», т.е. с построением «равносторонних прямоугольников» на сторонах прямоугольного треугольника, Фьеорованти попробовал построить на сторонах прямоугольного треугольника «равносторонние треугольники». Затем им были сделаны два обобщения этого построения: во-первых, равносторонние треугольники были построены на сторонах произвольного треугольника; во-вторых, была подмечена взаимосвязь внутреннего и внешнего треугольников Наполеона. Таким образом, название «треугольники Наполеона» этому построению было дано по аналогии с построениями Пифагора, и к императору Наполеону Бонапарту эти треугольники никакого отношения не имеют.

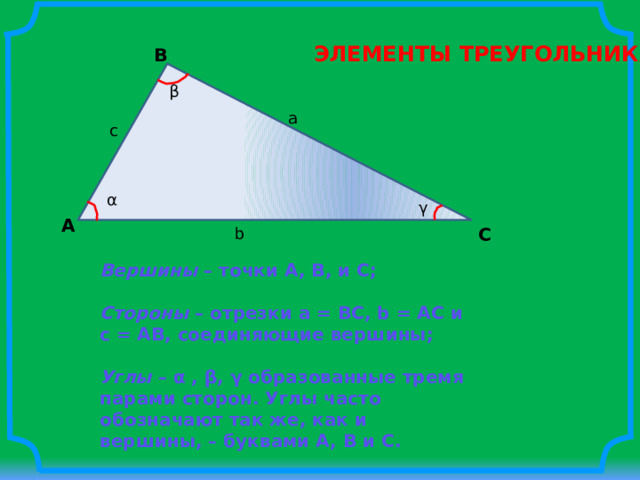
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА

B

β

a

c

α

γ

A

C

b

Вершины – точки A, B, и C;

Стороны – отрезки a = BC, b = AC и c = AB, соединяющие вершины;

Углы – α , β, γ образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, – буквами A, B и C.

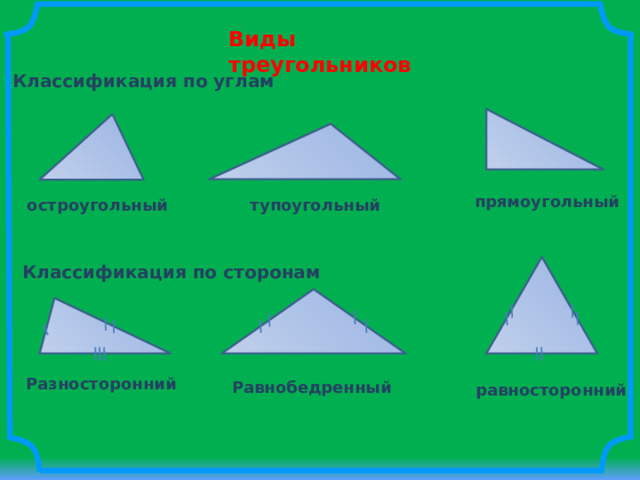
Виды треугольников

Классификация по углам

прямоугольный

тупоугольный

остроугольный

Классификация по сторонам

Разносторонний

Равнобедренный

равносторонний

Три высоты в треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

B

c

a

O

A

b

C

В остроугольном треугольнике ортоцентр лежит внутри треугольника, в прямоугольном - совпадает с вершиной прямого угла, а в тупоугольном треугольнике - находится вне треугольника на пересечении продолжений высот

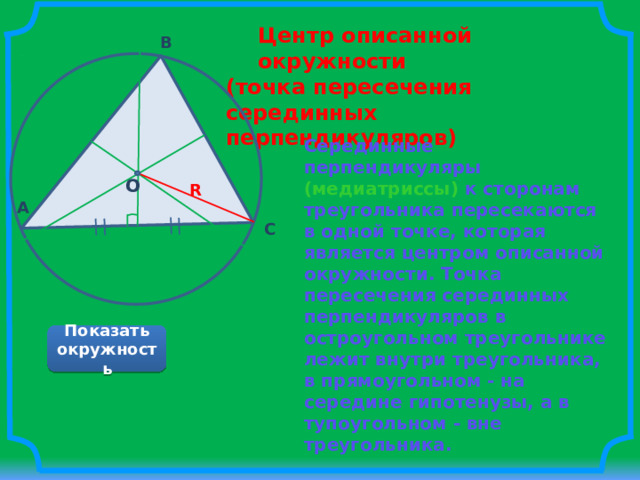
Центр описанной окружности

(точка пересечения серединных перпендикуляров)

B

Серединные перпендикуляры (медиатриссы) к сторонам треугольника пересекаются в одной точке, которая является центром описанной окружности. Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника, в прямоугольном - на середине гипотенузы, а в тупоугольном - вне треугольника.

О – центр окружности;

R – радиус окружности.

O

R

A

C

Показать окружность

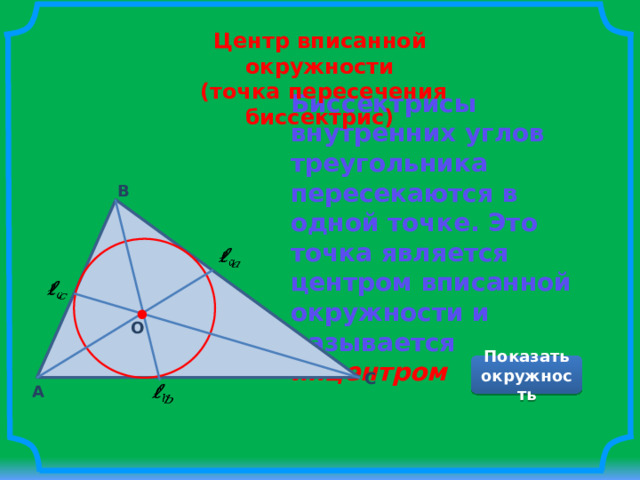
Центр вписанной окружности

(точка пересечения биссектрис)

Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка является центром вписанной окружности и называется инцентром

B

O

Показать окружность

C

A

B

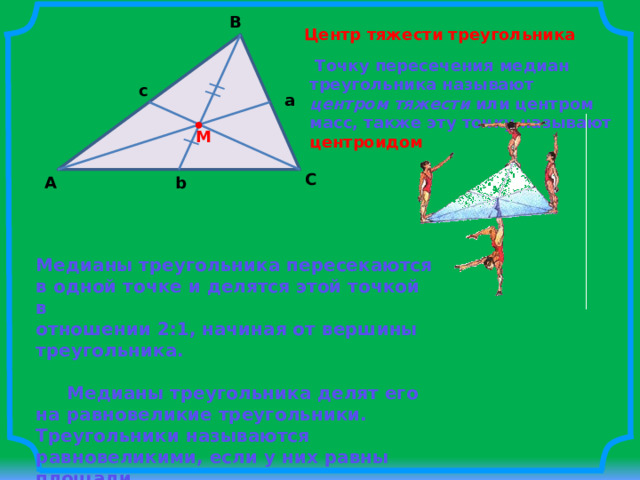
Центр тяжести треугольника

Точку пересечения медиан треугольника называют центром тяжести или центром масс, также эту точку называют центроидом

c

a

M

C

b

A

Медианы треугольника пересекаются в одной точке и делятся этой точкой в

отношении 2:1, начиная от вершины треугольника.

Медианы треугольника делят его на равновеликие треугольники. Треугольники называются равновеликими, если у них равны площади.

B

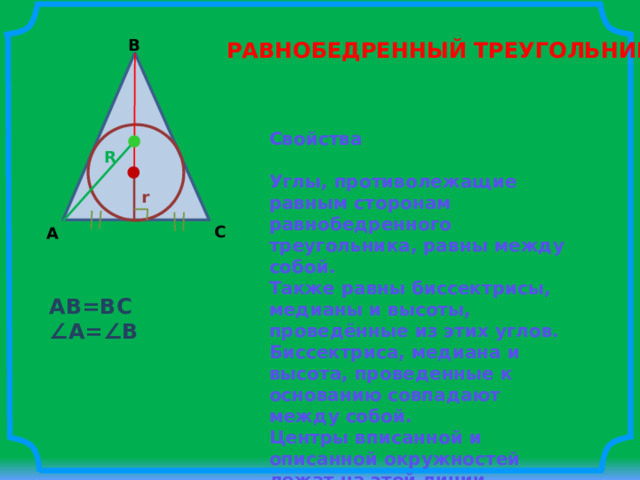
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК

Свойства

Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.

Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана и высота, проведенные к основанию совпадают между собой.

Центры вписанной и описанной окружностей лежат на этой линии.

Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).

R

r

C

A

AB=BC

∠ A=∠B

B

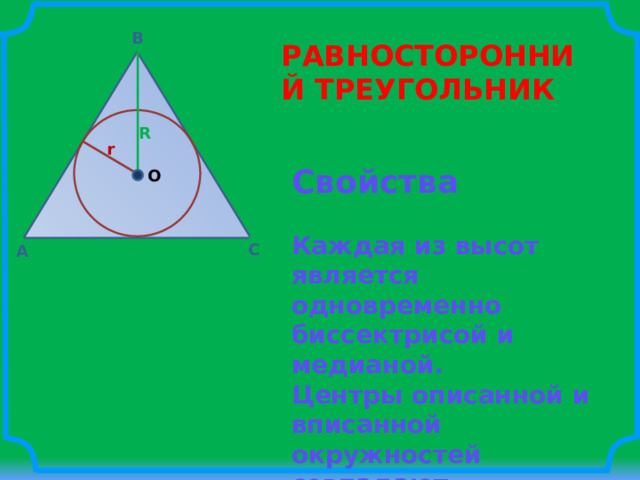
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК

R

r

Свойства

Каждая из высот является одновременно биссектрисой и медианой.

Центры описанной и вписанной окружностей совпадают.

O

C

A

C

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

b

a

h

A

b c

a c

B

c

Свойства

  1.Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).

2.Сумма двух острых углов прямоугольного треугольника равна прямому углу.

3.Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.

4.Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.

5.Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

B

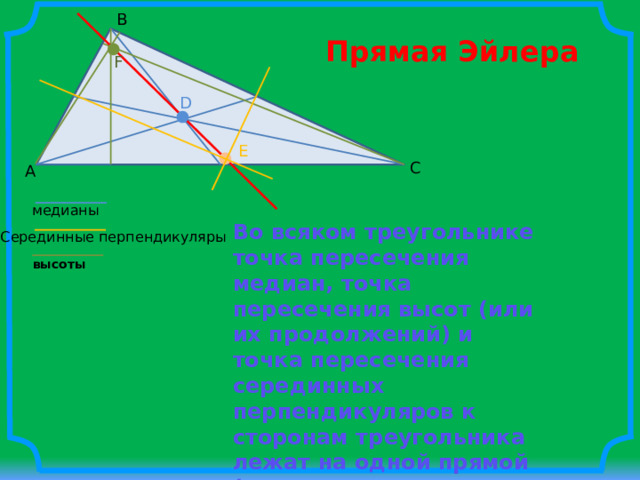
Прямая Эйлера

F

D

E

C

A

медианы

Во всяком треугольнике точка пересечения медиан, точка пересечения высот (или их продолжений) и точка пересечения серединных перпендикуляров к сторонам треугольника лежат на одной прямой (эта прямая называется прямой Эйлера )

Серединные перпендикуляры

высоты

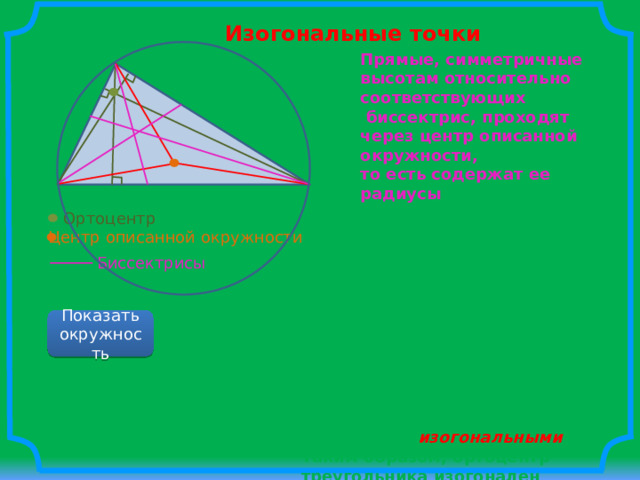
Изогональные точки

Прямые, симметричные высотам относительно соответствующих

биссектрис, проходят через центр описанной окружности,

то есть содержат ее радиусы

Ортоцентр

Справедливо также следующее: если три прямые, проведенные из вершин треугольника, пересекаются в одной точке, то и прямые, симметричные им относительно соответствующих биссектрис, тоже проходят через одну и ту же точку.

Подобные две точки называются изогональными . Таким образом, ортоцентр треугольника изогонален центру описанной окружности.

Центр описанной окружности

Биссектрисы

Показать окружность

Окружность девяти точек

B

Середины сторон треугольника

(точки A, B и С), основания

его высот (точки D, E и F)

и середины отрезков от вершин до ортоцентра

(точки M, K и H)

лежат на одной окружности.

.

.

S

L

O

.

N

A

C

Ее радиус равен половине радиуса описанной окружности (отрезок NL), а центр О лежит посередине отрезка NS, где N - центр описанной окружности, а точка

S - ортоцентр треугольника. Такая окружность называется окружностью девяти точек, или окружностью Эйлера, или окружностью Фейербаха - по имени Карла Фейербаха, провинциального учителя математики из Германии, родного брата философа Людвига Фейербаха

B

Точка Жергонна

O

J

A

C

Три отрезка, соединяющие вершины треугольника с точками, в которых вписанная в него окружность касается соответственно противоположных вершинам сторон, пересекаются в одной точке J. Она называется точкой Жергонна

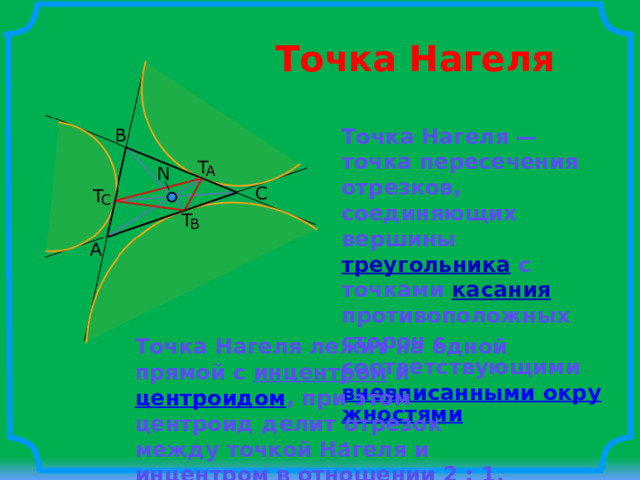
Точка Нагеля

Точка Нагеля — точка пересечения отрезков, соединяющих вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями .

Точка Нагеля лежит на одной прямой с инцентром и центроидом , при этом центроид делит отрезок между точкой Нагеля и инцентром в отношении 2 : 1.

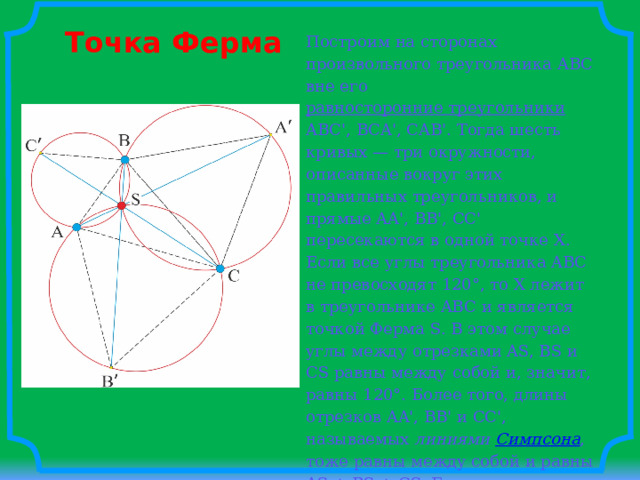
Точка Ферма

Построим на сторонах произвольного треугольника ABC вне его равносторонние треугольники ABC', BCA', CAB'. Тогда шесть кривых — три окружности, описанные вокруг этих правильных треугольников, и прямые AA', BB', CC' пересекаются в одной точке X. Если все углы треугольника ABC не превосходят 120°, то X лежит в треугольнике ABC и является точкой Ферма S. В этом случае углы между отрезками AS, BS и CS равны между собой и, значит, равны 120°. Более того, длины отрезков AA', BB' и CC', называемых линиями Симпсона , тоже равны между собой и равны AS + BS + CS. Если один из углов треугольника ABC больше 120°, то X лежит вне треугольника ABC, а точка Ферма S совпадает с вершиной тупого угла .

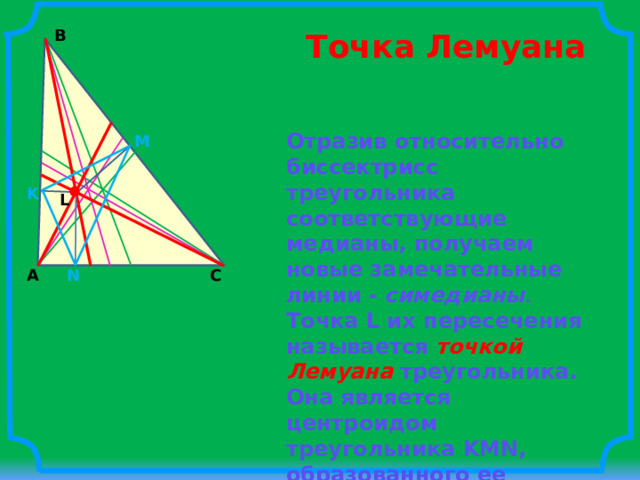
B

Точка Лемуана

Отразив относительно биссектрисс треугольника соответствующие медианы, получаем новые замечательные линии - симедианы .

Точка L их пересечения называется точкой Лемуана треугольника. Она является центроидом треугольника KMN, образованного ее проекциями на стороны исходного треугольника

M

K

L

N

A

C

Точка Брокара

C 1

B

A 1

Если на сторонах треугольника АВС внешним образом построить подобные ему треугольники СА1В, САВ1 и С1АВ (углы при первых вершинах всех четырех треугольников равны и т.д.), то прямые АА1, ВВ1 и СС1 пересекутся в точке Р, которую называют точкой Брокара . Одна из особенностей этой точки состоит в том, что угол РАС равен углу РСВ и равен углу РВА.

P

O

C

A

B 1

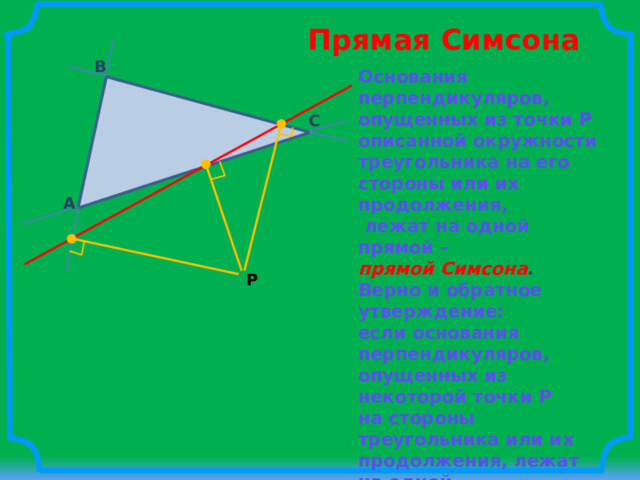
Прямая Симсона

B

Основания перпендикуляров,

опущенных из точки P описанной окружности треугольника на его

стороны или их продолжения,

лежат на одной прямой –

прямой Симсона .

Верно и обратное утверждение:

если основания перпендикуляров, опущенных из некоторой точки P

на стороны треугольника или их продолжения, лежат на одной

прямой, то точка P лежит на

описанной окружности треугольника.

C

A

P

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Атанасян Л. С. Геометрия: Учеб. для общеобразоват. учреждений. – М. : Просвещение, 2008.

2. Большая математическая энциклопедия / Якушева Г.М. и др. – М.: Филол.

О-во «СЛОВО»: ОЛМА-ПРЕСС, 2005. – 639 с.: ил.

3. Возникновение и развитие математической науки: Кн. Для учителя. – М.: Просвещение, 1987. – 159 с.: ил.

4. За страницами учебника алгебры: Кн. для учащихся 7 – 9 кл. сред. Шк. - М.: Просвещение, 1990. – 224 с.: ил.

5. Панов В. Ф. Математика древняя и юная/ Под ред. В. С. Зарубина. – 2-е изд., испр. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. – 648с.

6. Энциклопедия для детей. Т.11.Математика / Глав. ред, М. Д. Аксёнова. – М.: Аванта+,1998. – 688 с.: ил.

7. Энциклопедия. Мудрость тысячелетий. – М.: ОЛМА-ПРЕСС, 2004. –

Автор-составитель В. Балязин. – 848 с.