Прямоугольная система координат в профессиях

Муниципальное бюджетное образовательное учреждение

«Новоаганская общеобразовательная средняя школа № 2».

Проектная работа

Прямоугольная система

координат

Выполнил: ученик 8б класса

Клюев Данил

Руководитель: учитель математики

Клюева Лариса Валентиновна

2014 год.

Содержание:

1. Паспорт проекта…………………………………………………..3 стр

2. Аннотация…………………………………………………………5 стр

3. Введение: «Координаты вокруг нас»…………………………...6 стр

4. История создания системы координат……………………………………7 стр

5. Виды систем координат………………………………………………….8 стр

6. Построения в прямоугольной системе координат……………..9 стр

7. Заключение………………………………………………………13 стр

ПАСПОРТ ПРОЕКТА

1. Название проекта: "Прямоугольная система координат».

2. Руководитель проекта: Клюева Лариса Валентиновна

3. Учебный предмет, в рамках которого проводится работа по проекту: математика.

4.Учебные дисциплины, близкие к теме проекта: информатика, география.

5. Возраст учащихся, на который рассчитан проект: 12 – 14лет.

6. Тип проекта: информационно-поисковый

7. Цель проекта:

помочь ученикам нашего класса лучше понять тему «Координатная плоскость»;

показать использование координат в практических целях и в жизни человека;

подобрать материал, для создания электронных карточек по теме «Построения в прямоугольной системе координат»

8. Задачи проекта:

познакомиться с историей возникновения координатной плоскости;

расширить область познания в рамках выбранной темы;

создать дидактический материал в помощь учащимся и учителям математики по теме: «Построения в прямоугольной системе координат».

9. Вопросы проекта:

1) Зачем нужны координаты в жизни человека?

2) Кто ввел координаты и создал систему координат?

3) Какие построения можно выполнять в прямоугольной системе координат?

10. Необходимое оборудование: персональный компьютер, проектор, экран.

11. Актуальность проекта: работа в прямоугольной системе координат предполагает ее вычерчивание, а построение единичного отрезка – работу с измерительными приборами, что позволяет сочетать зрительную и мыслительную деятельность. Задачи с координатной плоскостью, интересны и разнообразны, что способствует лучшему усвоению темы, развивает интерес к предмету.

12. Этапы работы над проектом:

 Определение темы проекта.

 Сбор и систематизация материалов в соответствии с темой.

 Анализ полученных знаний, оформление проекта, создание презентации, создание папки с дидактическими материалами

 Представление и защита проекта.

13. Список использованных информационных ресурсов:

• Справочная литература

• Интернет

АННОТАЦИЯ

Координаты встречаются в нашей жизни ежечасно.

Система координат применяется в кинотеатре, на транспорте, в географии существует система координат.

Системы координат встречаются только с двумя величинами?

В морской бой все умеют играть все, и в этой игре применяются координаты.

Как летчики ориентируются в небе?

Положение звезд, наверное, тоже имеет координаты?

Это все встречается в современной жизни.

Но интересен такой факт, как давно система координат пронизывает практическую жизнь человека?

А какие построения можно выполнять в координатной плоскости?

Гипотеза проекта: «Знать, чтобы уметь»

Введение.

« В чистой математике живет всегда художник:

архитектор и даже поэт ».

Принсгейм А.

1. Координаты вокруг нас.

В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Собеседник просит записать свой адрес или номер телефона.

У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда.

Играя в игры, нам приходится определять местоположение «вражеского» корабля, фигуры на шахматной доске.

Разные ситуации? Но суть координат, что в переводе с греческого означает «упорядоченный» или, как обычно говорят, системы координат одно: это правило, по которому определяется положение того или иного объекта.

Слово «система» также греческого происхождения: «Тема» — нечто заданное, «сис» — составленное из частей. Таким образом, «система» - нечто заданное, составленное из частей (или четко расчлененное целое).

Системы координат пронизывают всю практическую жизнь человека. Например, по географической карте с помощью географических координат можно определить адрес любой точки. Для этого необходимо знать две части адреса — широту и долготу. Широту определяем с помощью «параллели» — воображаемой линии на поверхности Земли, проведенной на одинаковом расстоянии от экватора. Долгота — по «меридиану » — воображаемой линии на поверхности Земли, соединяющей Северный и Южный полюсы по кратчайшему расстоянию. Параллели — это линии направления запад — восток, меридианы показывают направление север — юг.

А как летчики ориентируются в небе? Положение звезд на небе тоже имеет координаты?

Это все встречается в современной жизни. Но интересен такой факт, как давно система координат пронизывает практическую жизнь человека?

История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции.
Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.

Уже во II в. древнегреческий астроном Клавдий Птоломей пользовался широтой и долготой в качестве координат.
Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. В декартовой системе координат получили реальное истолкование отрицательные числа.
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти.

Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

Термины «абсцисса» и «ордината» (образованные от латинских слов «отсекаемый» и «упорядоченный») были введены в 70-80 гг. XVII в. немецким математиком Вильгельмом Лейбницем.

3. Виды систем координат.

Положение любой точки в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат.

Числа, определяющие положение точки, называются координатами этой точки.

Наиболее употребительные координатные системы – декартовы прямоугольные.

Кроме прямоугольных систем координат существуют косоугольные системы. Прямоугольные и косоугольные координатные системы объединяются под названием декартовых систем координат.

Иногда на плоскости применяют полярные системы координат, а в пространстве – цилиндрические или сферические системы координат.

Обобщением всех перечисленных систем координат являются криволинейные системы координат.

« Красивые задания по теме «Координатная плоскость»

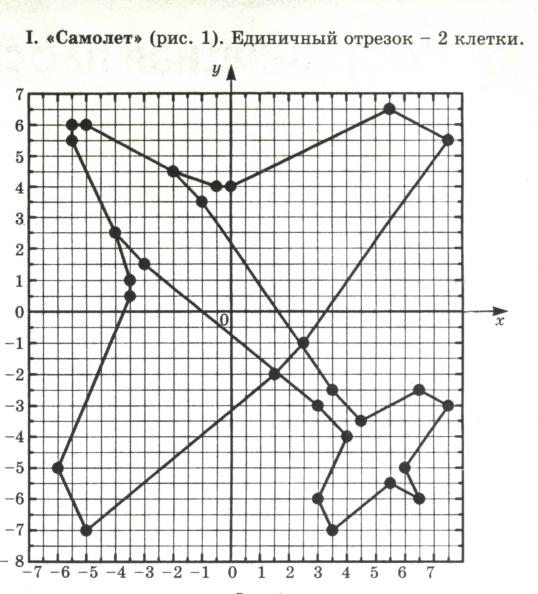
I. «Самолёт». Единичный отрезок – 2 клетки.

(-2; 4,5), (-0,5; 4), (0; 4), (5,5; 6,5), (7,5; 5,5), (2,5; -1), (1,5; - 2), (- 5; - 7), (- 6; - 5), (-3,5; 0,5), (-3,5; 1), (-4; 2,5), (-5,5; 5,5) , (-5,5; 6), (-5; 6), (-2; 4,5), (-1; 3,5), (3,5; -2,5), (4,5; -3,5), (6,5;-2,5), (7,5;-3), (6;-5), (6,5;-6), (5,5;-5,5), (3,5;-7), (3;-6), (4;-4), (3;- 3), (-3; 1,5),(-4; 2,5).

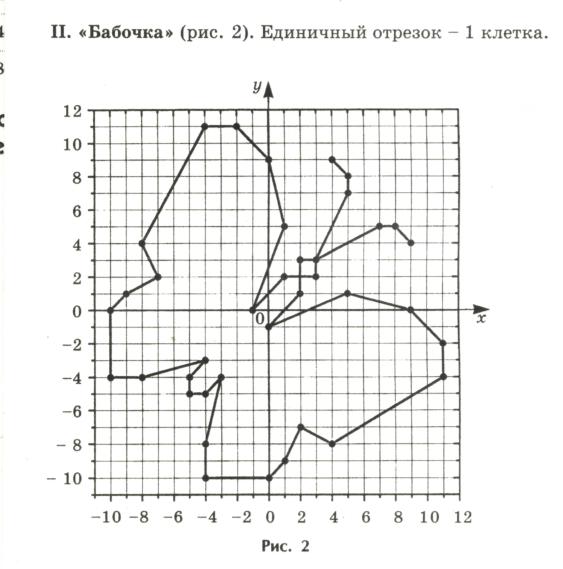
II. «Бабочка». Единичный отрезок – 1клетка.

(4; 9), (5; 8), (5; 7), (3; 3), (2;3), (2;1), (0;-1), (5; 1), (9; 0), (11;-2), (11;-4), (4;-8), (2;-7), (1; -9), (0; -10), (-4;-10), (-4;-8), (-3;-4), (-4;-5), (-5;-5), (-5;-4), (-4;-3), (-8;-4), (-10; -4), (-10;0),(-9;-1), (-7; 2), (-8; 4), (-4; 11), (-2; 11), (0; 9), (1; 5), (-1; 0), (1; 2), (3; 2), (3; 3), (7; 5), (8; 5), (9; 4).

III. «Воробей». Единичный отрезок – 1клетка.

(-6; 7), (-5; 8), (-4,5; 9), (-3; 9,5), (-1; 9), (0; 6), (1; 5), (4; 7), (7; 8), (9; 6), (12; 2), (13; 1), (7; 1), (5; -1), (6; -3), (8; -4), (11; -5), (13; -6), (12; -7), (11; -8), (9; -10), (8; -11), (7; -9), (6; -6), (5; -4), (-2; -2), (-7; -2), (-12; -5), (-11; 1), (-10; 3), (-7; 4), (-3; 4), (-4; 6), (-5; 7), (-6; 7).

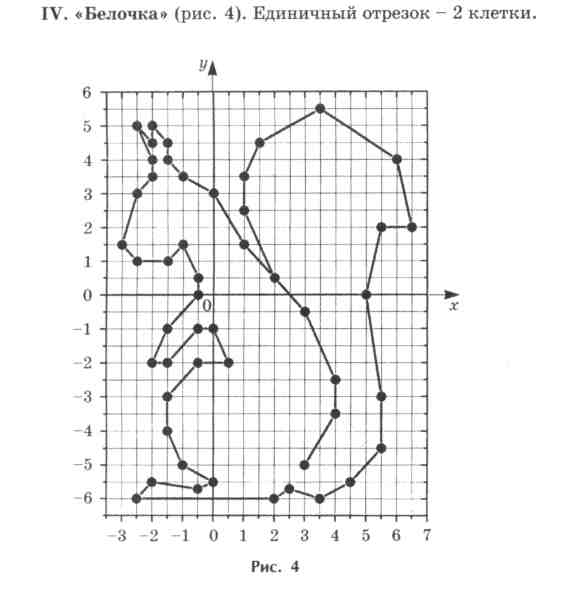
IY. «Белочка». Единичный отрезок – 2 клетки.

(3; -5), (4; -3,5), (4; -2,5), (3; -0,5), (2; 0,5), (3; 1,5), (0; 3), (-1; 3.5), (-1,5; 4), (1,5; 4,5), (-2; 5), (-2; 4,5), (-2,5; 5), (-2; 4), (-2; 3,5), (-2,5; 3), (-3; 1,5), (-1,5; 1), (-1; 1,5), (-0,5; 0,5), (-0,5; 0), (-1,5; -1), (-2; -2), (-1,5; -2), (-0,5; -1), (0; -1), (0,5, -2), (-0,5; -2), (-1,5; -3), (-1,5; -4), (-1; -5), (0; -5,5), (-0,5; -5,7), (-2; -5,5), (-2,5; -6), (2; -6), (2,5; -5,7), (3,5; -6), (4,5; -5,5), (5,5; -4,5), (5,5; -3), (5; 0), (5,5; 2), (6,5; 2), (6; 4); (3,5; 5,5), (1,5; 4,5), (1; 3,5), (1; 2,5), (2; 0,5).

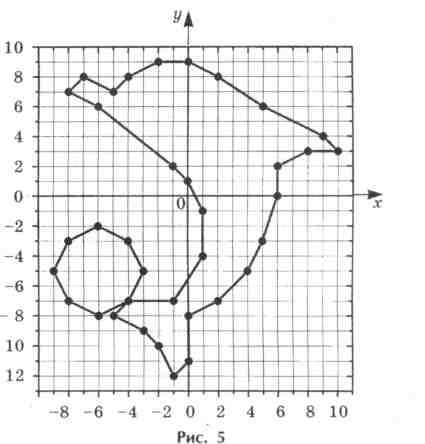
Y. «Дельфин». Единичный отрезок – 1клетка.

(-8; 7), (-7; 8), (-5; 7), (-4; 8), (-2; 9), (0; 9), (2; 8), (5; 6), (9; 4), (10; 3), (8; 3), (6; 2), (6; 0),

(5; -3), (4; -5), (2; -7), (0; -8), (0; -11), (-1; -12), (-2; -10), (-3; -9), (-5; -8), (-4; -7), (-3; -5),

(-4; -3), (-6; -2), (-8; -3), (-9; -5), (-8; -7), (-6; -8), (-4; -7), (-1; -7), (1; -4), (1; -1), (0; 1),

(-1; 2), (-6; 6), (-8; 7).

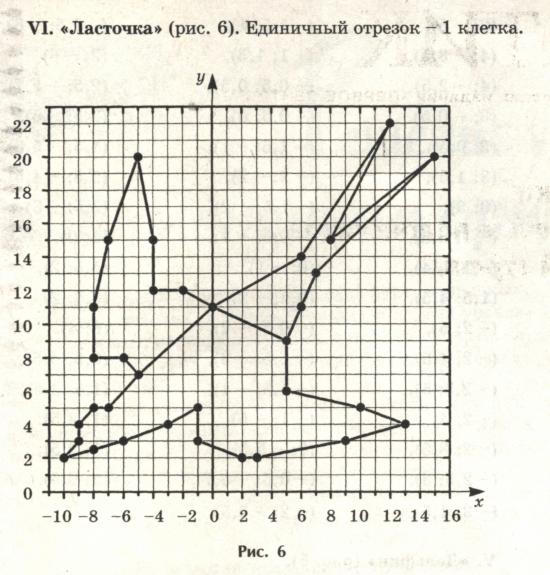
YI. «Ласточка». Единичный отрезок – 1клетка.

(5; 9), (5; 6), (10; 5), (13; 4), (9; 3), (3; 2), (2; 2), (-1; 3), (-1; 5), (-3; 4), (-6; -3), (-8; 2,5), (-10;2), (-9; 3), (-9; 4), (-8; 5), (-7; 5), (-5; 7), (0; 11), (7; 15), (12; 22), (9; 16),

(15; 20), (8; 14), (6; 11), (5; 9), (0;11), (-2; 12), (-4; 12), (-4; 15), (-5;20), (-7; 15), (-8; 11), (-8; 8), (-6; 8), (-5; 7).

YII. «Сорока». Единичный отрезок – 1клетка.

(-9; 1,5), (-7; 1,8), (-6; 2), (-5; 2), (-3; 1), (0; 1), (2; 2), (4; 5), (5; 7), (7; 8), (9; 8), (9; 7), (10; 7), (10; 5), (9; 3), (4; 0), (3; -1), (4; -4), (5; -5),(1; -5), (-1; -4), (0,5; -4,7), (0; -5),

(-3; -4), (-7; 0), (-9; 0), (-8; 0,5), (-7; 0,1), (-7,5; 1), (-9; 1,5).

Лапы: (-5; -4), (-3; -4), (-4; -5), (-4; -6), (0; -6) и (-4; -7), (0; -5).

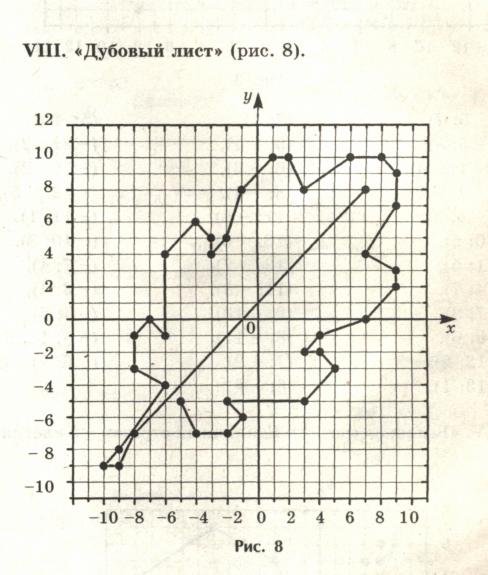
YIII. «Дубовый лист». Единичный отрезок – 1клетка.

(7; 8), (-8; -7), (-9; -9), (-10; -9), (-9; -8), (-6; -4), (-8; -3), (-8; -1), (-7; 0), (-6; -1),

(-6; 4), (-4; 6), (-3; 5), (-3; 4), (-2; 5), (-1; 8), (1; 10), (2; 10), (3; 8), (6; 10), (8; 10), (9; 9), (9; 7), (7; 4), (9; 3), (9; 2), (7; 0), (4; -1), (3; -2), (4; -2), (5;-3), (3; -5), (-2;-5), (-1;-6),

(-2;-7), (-4;-7), (-5; -5).

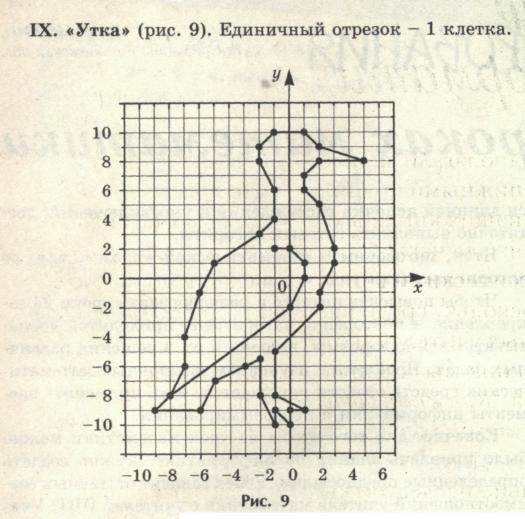
IX. «Утка». Единичный отрезок – 1клетка.

(-1; 2), (0; 2), (1; 1), (1; 0), (0; -2), (-8; -8), (-7; -6), (-7; -4), (-6; -1), (-5; 1), (-1; 5),

(-2; 8), (-2; 9), (-1; 10), (1; 10), (2; 9), (5; 8), (2; 8), (1; 7), (2; 5), (3; 2), (3; 1), (2; -1), (2; -2), (-1; -5), (-1; -8), (1; -9), (0; -10), (-1; -9), (-1; -10), (-2; -8), (-2; 5,5), (-5; -7),

(-6; -9), (-9; -9), (-8; -8).

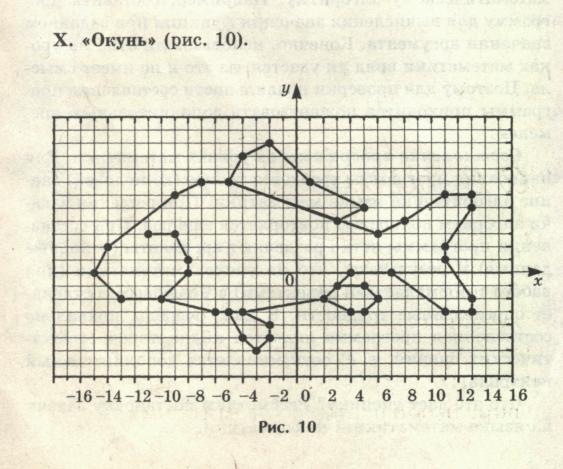
X. «Окунь». Единичный отрезок – 1клетка.

(-11; 3), (-9; 3), (-8; 1), (-8; 0), (-10; -2), (-13;-2), (-15; 0), (-14; 2), (-9; 6), (-7; 7), (-5; 7), (3; 4), (5; 5), (1; 7), (-2;10), (-4; 9), (-5; 7), (6; 3), (8; 4), (11; 6), (13; 6), (13; 5), (11; 2), (11; 1), (13; -2), (13; -3), (11; -3), (7; 0), (4; 0), (2; -2), (4;-3), (5;-3), (6;-2), (5;-1), (3;-1), (2;-2), (-4;-3), (-5; -3), (-4; -5), (-3; -6), (-2; -5), (-2; -4), (-4; -3), (-6; -3), (-10; -2).

Плавник:(-8; -1), (-6; 0), (-5; 0), (-4; -1),(-6; -2), (-8; -2).

Глаз: (-12; 1), (-12; 2), (-11; 2),(-11; 1), (-12; 1).

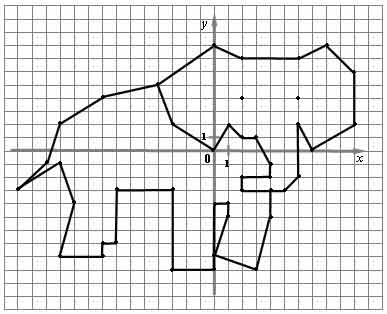
XI. Слоник. Единичный отрезок – 1клетка.

1. (2; - 3), (2; - 2), (4; - 2), (4; - 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5), (0; 8),

(2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; - 2), (5; - 3), (2; - 3).

2) (4; - 3), (4; - 5), (3; - 9), (0; - 8), (1; - 5), (1; - 4), (0; - 4), (0; - 9), (- 3; - 9), (- 3; - 3), (- 7; - 3), (- 7; - 7), (- 8; - 7), (- 8; - 8), (- 11; - 8), (- 10; - 4), (- 11; - 1), (- 14; - 3),
(- 12; - 1), (- 11;2), (- 8;4), (- 4;5).

3) Глаза: (2; 4), (6; 4).

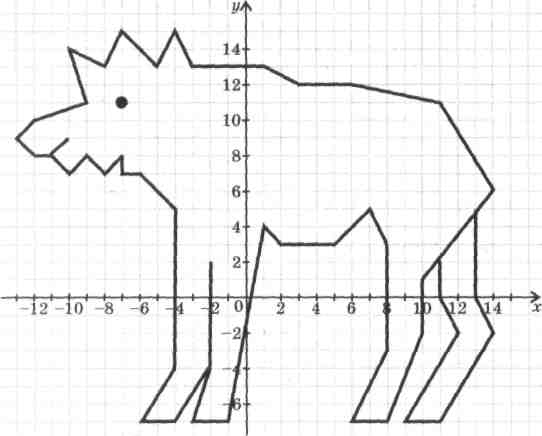
XII. Лось. Единичный отрезок – 1клетка.

(-2; 2), (-2; -4), (-3; -7), (-1; -7), (1; 4), (2; 3), (5; 3), (7; 5), (8; 3), (8; -3), (6; -7),

(8; -7), (10; -2), (10; 1), (11; 2,5), (11; 0), (12; -2), (9;-7), (11;-7), (14;-2), (13; 0),

(13; 5), (14;6), (11; 11),(6; 12),(3; 12),(1; 13),(-3; 13),(-4;15), (-5; 13), (-7; 15),

(-8; 13), (-10; 14), (-9; 11), (-12; 10), (-13; 9), (-12; -8), (-11; 8), (-10; 9), (-11; 8),

(-10; 7), (-9; 8), (-8; 7),(-7; 8), (-7; 7), (-6; 7), (-4; 5), (-4; -4), (-6; -7),(-4; -7), (-2; -4).

Соединить: (11; 2,5) и (13; 5).

Глаз: (-7; 11).

Заключение

Такая работа в прямоугольной системе координат позволяет не только лучше понять тему, но и дает возможность проявить творческие способности каждого из нас.

Трудно устоять перед соблазном и не нарисовать свои рисунки.

Результатом моей работы над проектом является дидактический материал, которым пользуются учащиеся и преподаватели нашей школы, и, надеюсь, будут пользоваться и в дальнейшем.

Литература

1. Колосов А. А. Книга для внеклассного чтения по математике. –учпедгиз.,Москва, 1963.

2. Глейзер А. А . История математики в школе.

3. Журнал «Математика в школе» №4-2005 г.

4. Виленкин «Математика-6 класс».

15