Прямоугольник, его свойства и признак

Прямоугольник

К учебнику Л.С.Атанасяна

Геометрия 7 - 9, Глава V, п. 46, 8 класс

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Какой четырехугольник называется прямоугольником?

Можно ли утверждать, что прямоугольник – это параллелограмм, и почему?

Чем отличается произвольный параллелограмм от прямоугольника?

Закончите предложение: « Прямоугольник – это параллелограмм, у которого …

все углы прямые

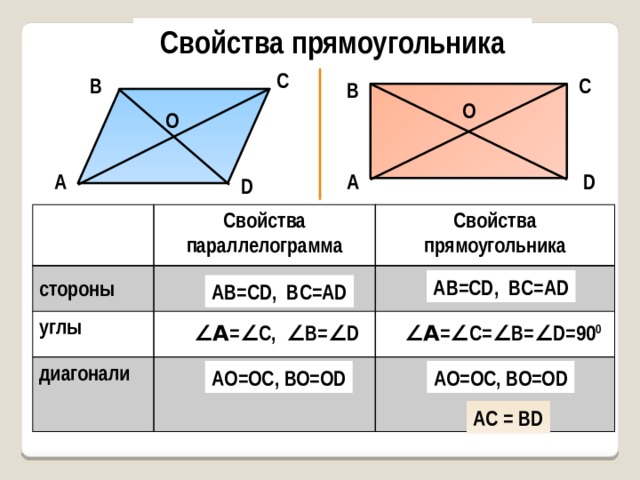
Свойства прямоугольника

С

С

В

В

О

О

А

А

D

D

стороны

Свойства параллелограмма

углы

Свойства прямоугольника

диагонали

АВ=CD, BC=AD

АВ=CD, BC=AD

∠ A = ∠ C, ∠ B= ∠ D

∠ A = ∠ C= ∠ B= ∠ D=90 0

AО=ОС, ВО=ОD

AО=ОС, ВО=ОD

AC = BD

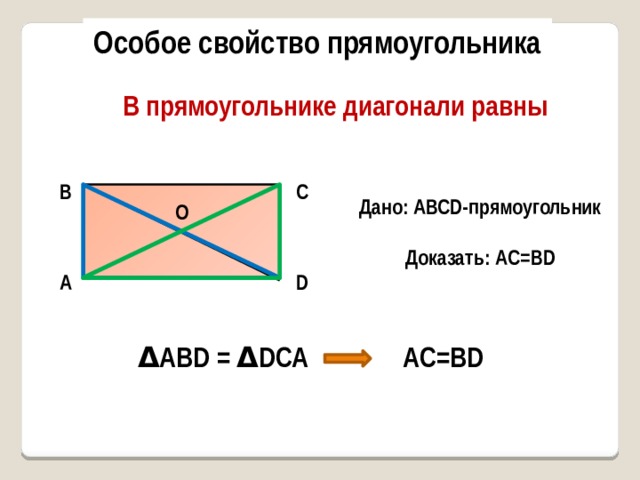
Особое свойство прямоугольника

В прямоугольнике диагонали равны

В

С

Дано: AВСD-прямоугольник

О

Доказать: AС=ВD

А

D

Δ AВD = Δ DСА

AС=ВD

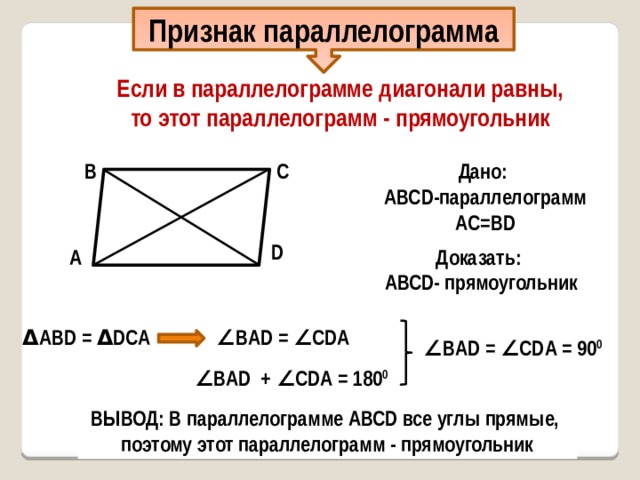
Признак параллелограмма

Если в параллелограмме диагонали равны,

то этот параллелограмм - прямоугольник

В

С

Дано:

AВСD-параллелограмм

AС=ВD

О

D

Доказать:

А

AВСD- прямоугольник

Δ AВD = Δ DСА

∠ ВAD = ∠ СDА

∠ ВAD = ∠ СDА = 90 0

∠ ВAD + ∠ СDА = 180 0

ВЫВОД: В параллелограмме АВСD все углы прямые,

поэтому этот параллелограмм - прямоугольник

Выберите верные

утверждения

1. Если в четырехугольнике диагонали равны и делятся точкой пересечения пополам, то этот четырехугольник - прямоугольник.

2. Если в четырехугольнике противоположные стороны параллельны, а все его углы прямые, то этот четырехугольник - прямоугольник.

3. Если в четырехугольнике диагонали равны, то этот четырехугольник - прямоугольник.

4. Если в параллелограмме два угла прямых, то этот параллелограмм - прямоугольник .

5. Если в четырехугольнике два прямых угла и две стороны равны, то этот четырехугольник - прямоугольник.

6. Если в четырехугольнике диагонали равны, а один угол прямой, то этот четырехугольник - прямоугольник.

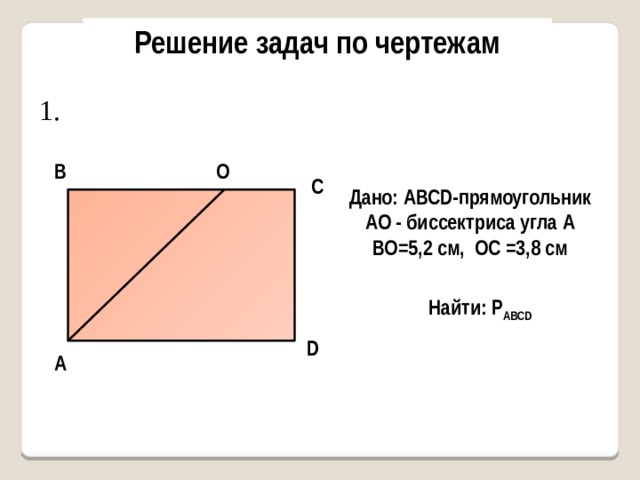
Решение задач по чертежам

1.

В

О

С

Дано: AВСD-прямоугольник

АО - биссектриса угла А

ВО=5,2 см, ОС =3,8 см

Найти: Р AВСD

D

А

Решение задач по чертежам

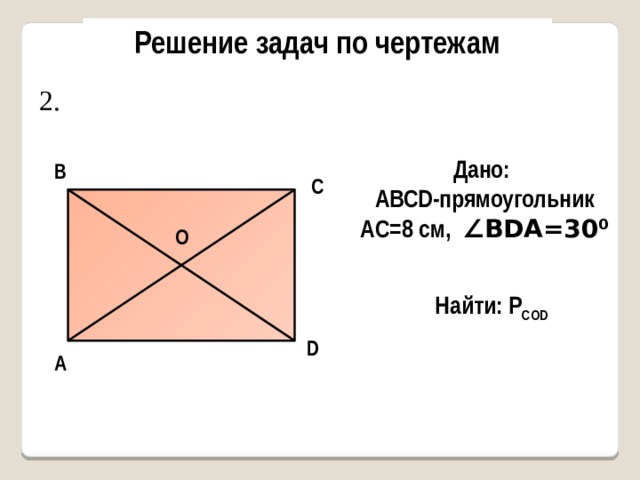
2.

Дано:

AВСD-прямоугольник

AC=8 см, ∠BDA=30 0

В

С

О

Найти: Р СOD

D

А

Решение задач по чертежам

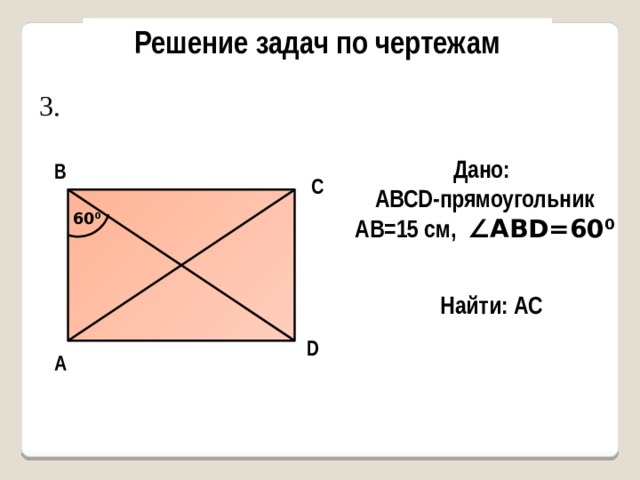
3.

Дано:

AВСD-прямоугольник

AB=15 см, ∠ABD=60 0

В

С

60 0

Найти: AC

D

А

Решение задач по чертежам

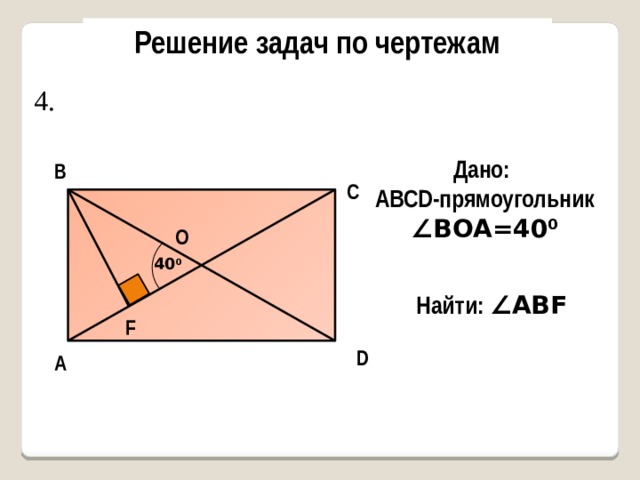
4.

Дано:

AВСD-прямоугольник

∠ BОA=40 0

В

С

О

40 0

Найти: ∠ABF

F

D

А

Решение задач по чертежам

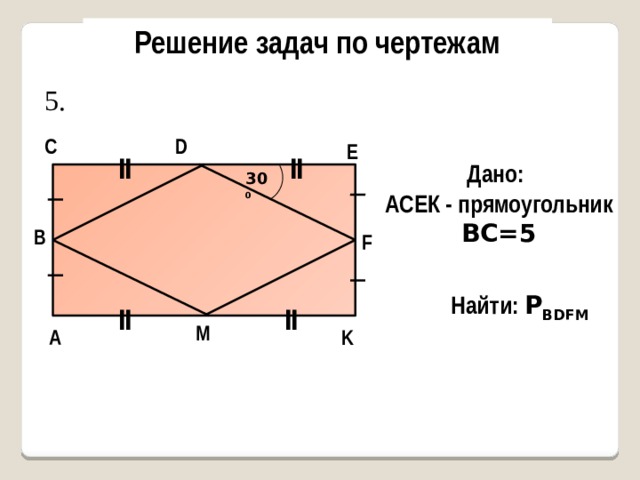
5.

С

D

E

ǁ

ǁ

Дано:

AСЕК - прямоугольник

ВС=5

30 0

В

F

Найти: Р BDFM

ǁ

ǁ

M

K

А

Решение задач по чертежам

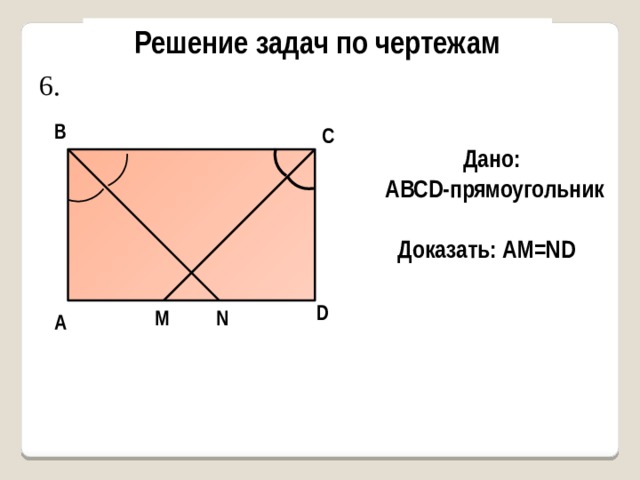
6.

В

С

Дано:

AВСD-прямоугольник

Доказать: AM=ND

D

N

M

А

Решение задач по чертежам

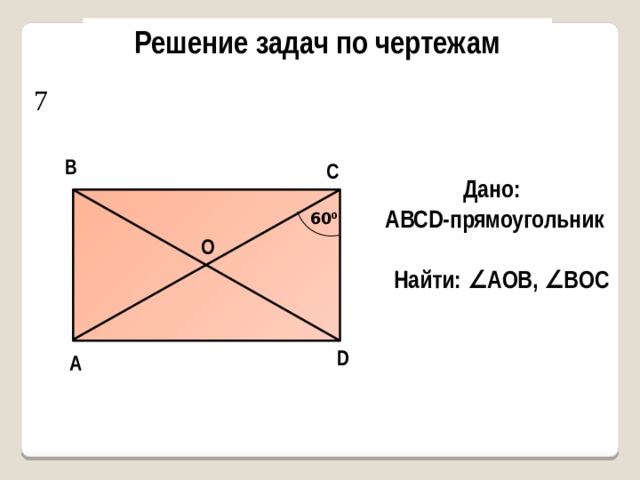
7

В

С

Дано:

AВСD-прямоугольник

60 0

О

Найти: ∠AОB, ∠BОС

D

А

Решение задач по чертежам

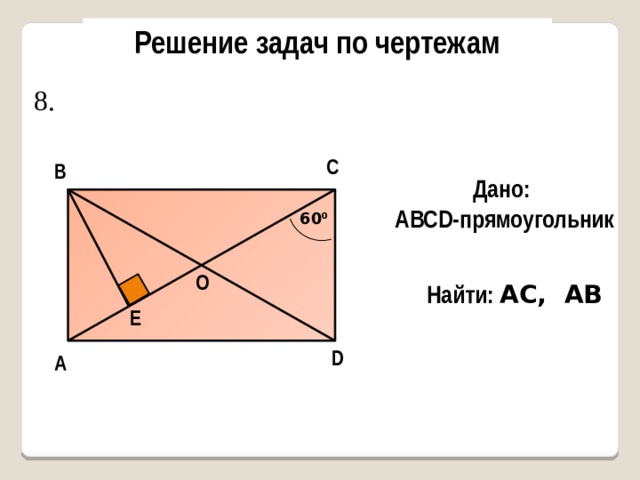
8.

С

В

Дано:

AВСD-прямоугольник

60 0

О

Найти: АС, AB

Е

D

А

4 см

6 см

Решение задач по чертежам

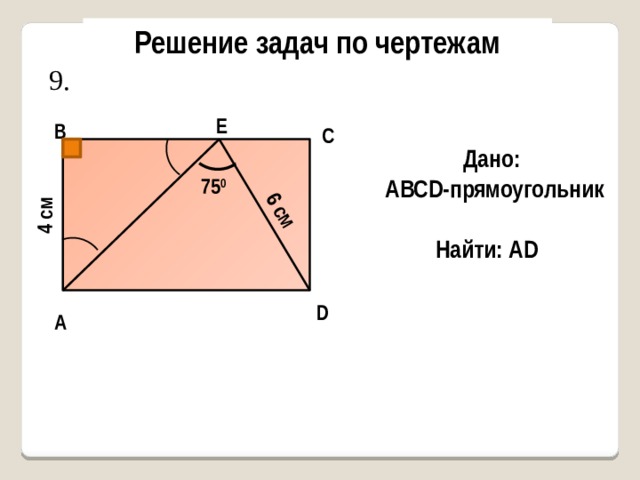
9.

Е

В

С

Дано:

AВСD-прямоугольник

75 0

Найти: AD

D

А

ǁ

ǁ

Решение задач по чертежам

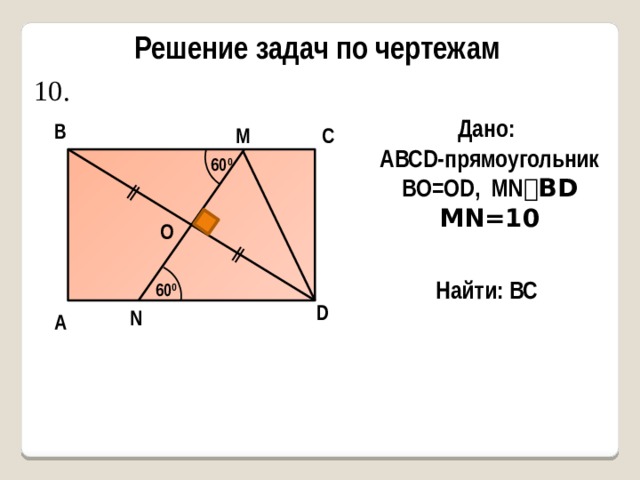
10.

Дано:

AВСD-прямоугольник

BO=OD, MN ⏊BD

MN=10

В

С

M

60 0

О

Найти: ВС

60 0

D

N

А

ǁ

ǁ

Решение задач по чертежам

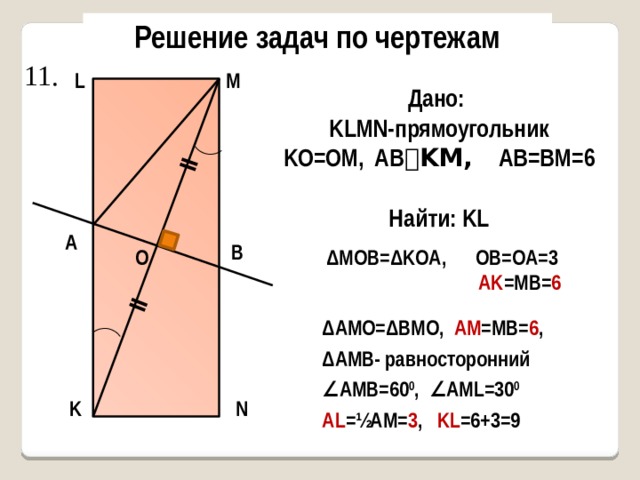
11.

L

M

Дано:

KLMN-прямоугольник

KO=OM, AB ⏊KM, AB=BM=6

Найти: KL

A

B

O

ΔMOB=ΔKOA, OB=OA=3

AK =MB= 6

ΔAMO=ΔBMO, AM =MB= 6 ,

ΔAMB- равносторонний

∠ АМВ=60 0 , ∠АМL=30 0

AL =½AM= 3 , KL =6+3=9

K

N

Найти: AC