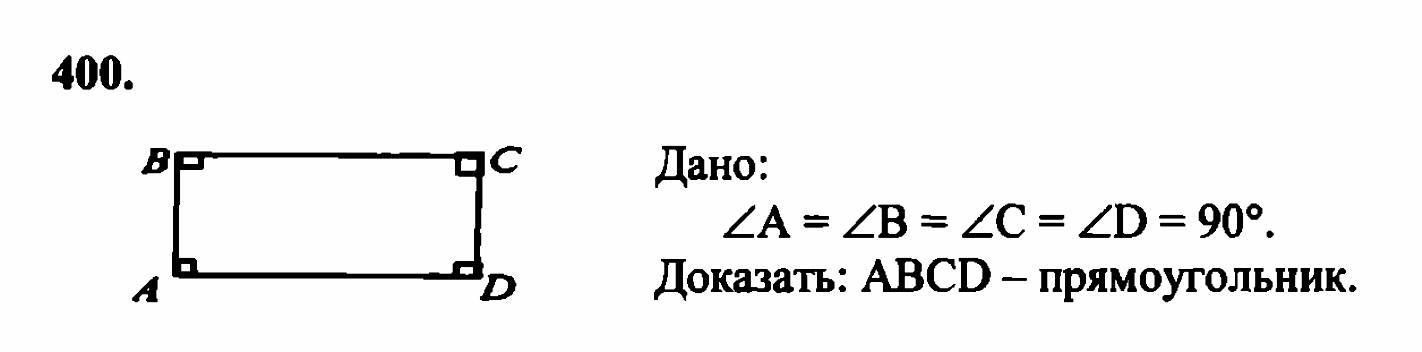Тема. Прямоугольник
Цели:
Обучающая:
дать определение «прямоугольника»;
рассмотреть свойства прямоугольника как частного вида параллелограмма;
продолжить формировать умения учащихся применять свойства и признаки параллелограмма при решении задач.
Развивающая:
развивать творческую и мыслительную деятельность, логическое мышление учащихся в процессе изучения нового материала и решения задач;
развивать познавательный интерес и любознательность учащихся, умения самостоятельно работать, излагать мысли грамотным математическим языком.
Воспитательная:
прививать учащимся интерес к предмету;
формировать умения аккуратно и грамотно выполнять математические записи и чертежи;
учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности.
Оборудование: интерактивная доска
Тип урока: урок изучения нового материала
Структура урока
Организационный момент (2 мин.)
Актуализация опорных знаний и умений учащихся (5 мин.)
Проверка домашнего задания (8 мин.)
Мотивация учебной деятельности учащихся (3 мин.)
Изучение нового материала (10 мин.)
Закрепление изученного (10 мин.)
Домашнее задание (3 мин.)
Подведение итогов урока (4 мин.)
Организационный момент
Сообщение темы и целей урока
Актуализация опорных знаний и умений учащихся
повторяем изученный материал по теме:
1. Продолжите предложение:
а) в параллелограмме противоположные стороны … (равны)
б) в параллелограмме противоположные углы … (равны)
с) диагонали параллелограмма точкой пересечения … (делятся пополам)
д) параллелограмм является … (выпуклым четырёхугольником)
е) сумма углов выпуклого четырёхугольника равна … (360)
ж) четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны, называется… (трапеция)
з) существуют такие виды трапеций: … (равнобокие и прямоугольные)
и) прямоугольная трапеция – это трапеция, у которой… (боковая сторона перпендикулярна основаниям).
2. Выберите те фигуры, которые являются четырёхугольниками, но не являются параллелограммами (какая это фигура?):





Проверка домашнего задания
Тема предыдущего урока – Трапеция
| Трапеция |
| 1. В равнобокой трапеции сумма углов при большем основании равна 96. Найдите углы трапеции. 2. В прямоугольной трапеции острый угол равен 45. Меньшая боковая сторона и меньшее основание равны по 10 см. Найдите большее основание. |
| Решение задач из домашнего задания форма проверки – коллективная |
| 1. В С 
 
А D
Так как в равнобокой трапеции углы при основании равны, то А=D=96:2=48. Так как АD и ВС параллельны, то сумма односторонних углов равна 180. Отсюда следует: В=180-48=132. С=132.
Ответ: 48, 48, 132, 132. |
| 2. АВСD – прямоугольная трапеция. По условию задачи АВ=ВС=10 см. D=45. Из вершины С опустим высоту СМ на сторону АD. Получили: АМ=СМ=10 см. Рассмотрим треугольник СМD. Он равнобедренный: С=180–90–45=45. Поэтому СМ=МD=10 см. АD=АМ+МD=20 см.
Ответ: большее основание 20 см. |
| При проверке домашнего задания (задача 1) можно использовать следующую методику: (к доске вызываются три ученика) 1. Один ученик записывает в первой колонке теоремы, которые используются при решении задачи в порядке логической необходимости. 2. Второй ученик на против каждой теоремы во второй колонке пишет математическое решение. 3. Третий ученик записывает ответ.
При проверке домашнего задания (задача 2) можно использовать следующую методику: учитель вызывает к доске по очереди учащихся, которые должны объяснить решение задачи. Каждого ученика учитель прерывает на определённом этапе хода объяснения решения задачи. Каждый следующий продолжает с места остановки предыдущего. Таким образом логически будет построена цепочка решения задачи несколькими учащимися. |
| За каждый правильный ответ – 2 б. (с учётом правильных ответов учащихся на вопросы на других этапах урока можно получить оценку «5»). |
Мотивация учебной деятельности учащихся
На доску проецируются следующие фигуры:








Среди предложенных четырехугольников учащиеся должны выбрать те, которые являются прямоугольниками.
Вопрос учителя: по каким признакам выбрали именно эту фигуру?
Изучение нового материала
На доске записаны свойства.
Задание 1. Какие из перечисленных здесь свойств определяют понятие параллелограмма, а какие – прямоугольника?
а) диагонали взаимно перпендикулярны и делят его углы пополам.
б) диагонали пересекаются и точкой пересечения делятся пополам.
в) диагонали равны между собой.
г) противоположные стороны попарно параллельны.
д) противоположные стороны и углы равны.
е) все углы прямые.
ж) все стороны равны.
Учащиеся заполняют таблицу, прочитав вышерасположенные свойства фигур:
| параллелограмм | прямоугольник | другая фигура |
| 
| 
|
? |
| б), г), д) | б), в), г), д), е) | а), ж) |
|
|
|
|
Учащиеся сравнивают параллелограмм и прямоугольник, и, возможно, при помощи учителя, записывают свойства четырёхугольников в таблицу соответственно фигуре. Учащиеся делают вывод, что свойства а) и ж) не принадлежат параллелограмму и прямоугольнику, и, возможно, они принадлежат неизвестному им ещё четырёхугольнику.
Заполнив таблицу, учащиеся делают вывод, что в колонке прямоугольника находятся те же свойства, что и в колонке параллелограмма. Учащиеся делают вывод, что прямоугольник – это параллелограмм. Внимательно изучив ещё раз записанное в колонке прямоугольника (здесь есть свойства, присущие только прямоугольнику), дети дают определение прямоугольника.
Прямоугольник – это параллелограмм, у которого все углы прямые.
Закрепление изученного
Учащиеся решают задачи на определение признаков прямоугольника.

АВСD – параллелограмм, следовательно, АВ=СD, ВС=АD.
А=С=90, В=D.
Так как А+В=180, то В=180 – 90=90.
Т.е. в АВСD стороны попарно равны; все углы прямые, значит, АВСD – прямоугольник.
Решив эту задачу, учащиеся формулируют теорему о признаке прямоугольника:
Теорема. Признак прямоугольника: Если в параллелограмме хотя бы один угол прямой, то он является прямоугольником.
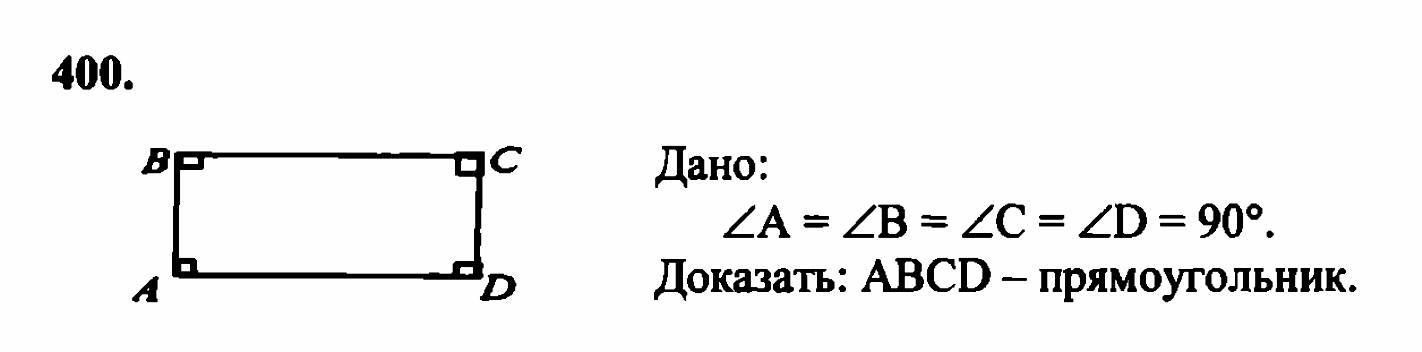
А+В=180. А, В – односторонние при АD и ВС и секущей АВ, следовательно АD и ВС параллельны. Аналогично, АВ и СD параллельны, В, С – односторонние при АВ, СD и секущей ВС. АD II ВС, АВ II СD, следовательно, АВСD – параллелограмм, А=В=С=Д=90, следовательно, АВСD – прямоугольник.
Решив эту задачу, учащиеся формулируют теорему о признаке прямоугольника:
Теорема. Признак прямоугольника: Если в четырёхугольнике все углы прямые, то он является прямоугольником.
Учащиеся записывают и другие теоремы о признаках прямоугольника:
Теорема. Признак прямоугольника: Если в параллелограмме все углы равны, то он является прямоугольником.
Теорема. Признак прямоугольника: Если в параллелограмме диагонали равны, то он является прямоугольником.
Домашнее задание
Прочитать по учебнику § 3, п. 46. Решить задачу № 402 и самостоятельно сформулировать теорему о свойстве диагоналей прямоугольника (Диагонали прямоугольника при пересечении делят его на четыре равнобедренных треугольника).
Подведение итогов урока
Учитель обращает внимание учащихся ещё раз на признаки прямоугольника. Учащиеся называют свойства этой фигуры.
Возвращаясь к таблице о свойствах параллелограмма и прямоугольника, внимание учащихся следует обратить на третью колонку с неизвестной фигурой. Учащиеся получают задание нарисовать фигуру по этим свойствам (диагонали взаимно перпендикулярны и делят его углы пополам, все стороны равны) и определить этот четырёхугольник. Учащиеся получают задание наперёд составить свойства полученной фигуры (для получения первичных представлений о ромбе).