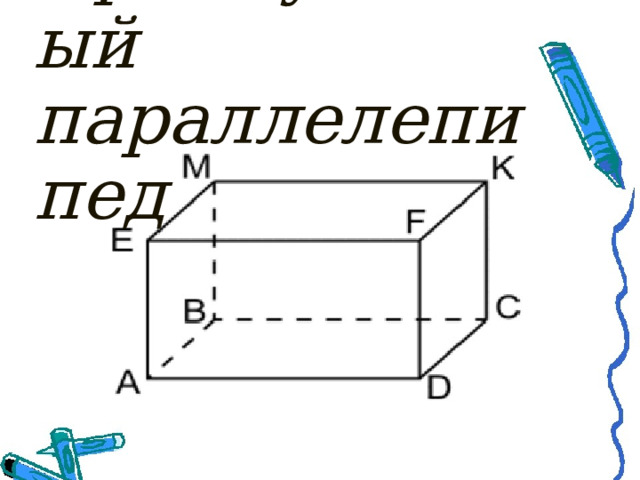
Прямоугольный параллелепипед

Цель урока:
-познакомиться с прямоугольным параллелепипедом, его элементами;
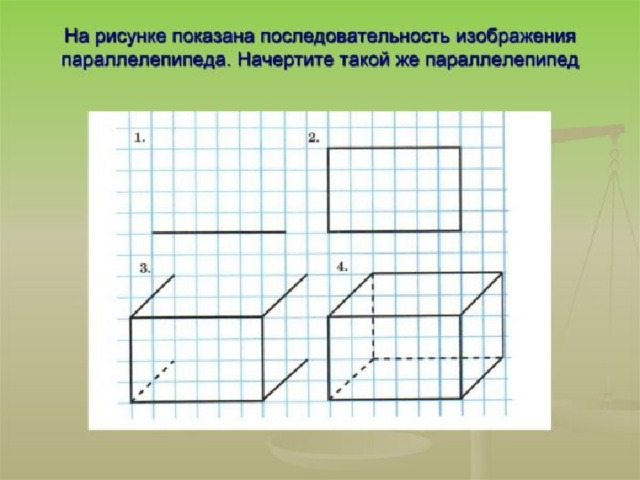
-научиться чертить прямоугольный параллелепипед;
- находить длину рёбер и площадь поверхности прямоугольного параллелепипеда
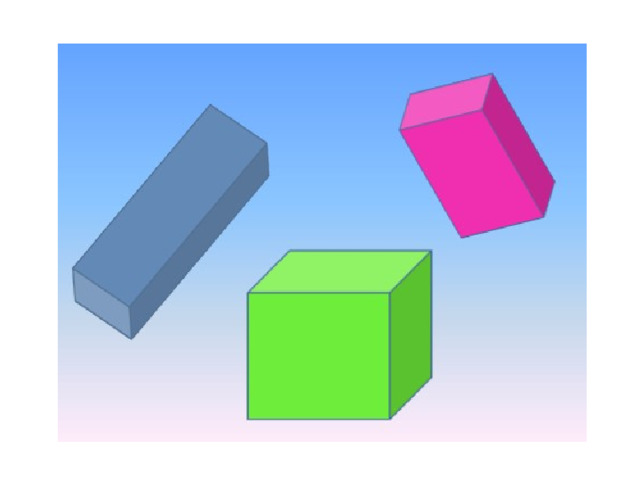

Прямоугольный параллелепипед в нашей жизни
Спичечный коробок, кирпич, шкаф, чемодан, здания, системный блок компьютера дают представление о прямоугольном параллелепипеде.

Познакомимся поближе с элементами прямоугольного параллелепипеда

Элементы прямоугольного параллелепипеда
Элемент
Форма
Общее количество
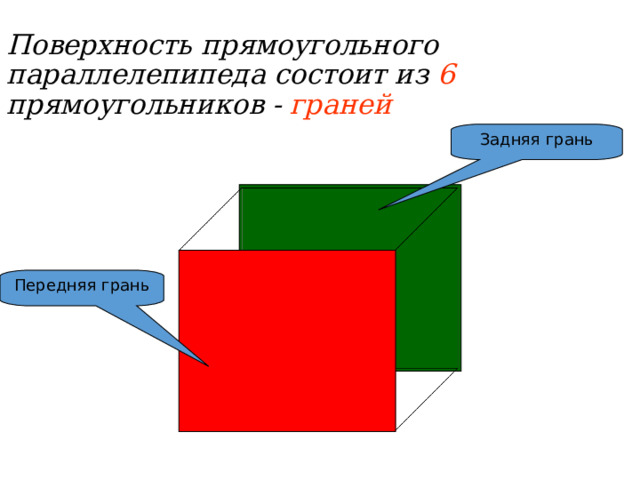
Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников - граней
Задняя грань
Передняя грань
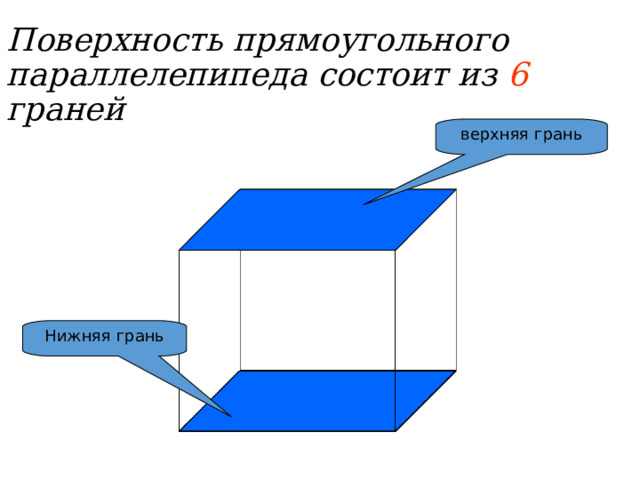
Поверхность прямоугольного параллелепипеда состоит из 6 граней
верхняя грань
Нижняя грань
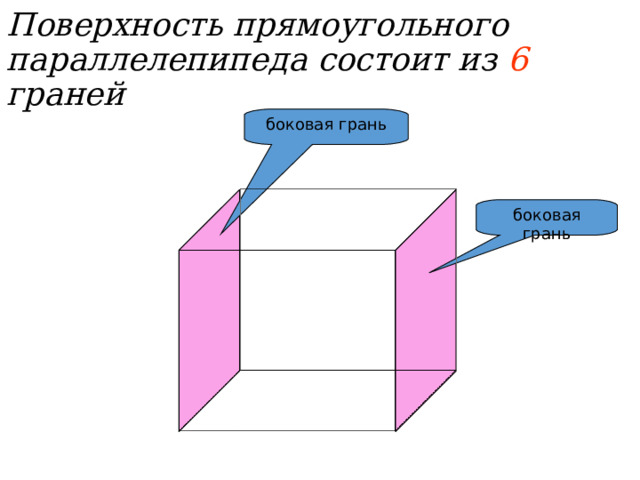
Поверхность прямоугольного параллелепипеда состоит из 6 граней
боковая грань
боковая грань

Противоположные
грани равны !
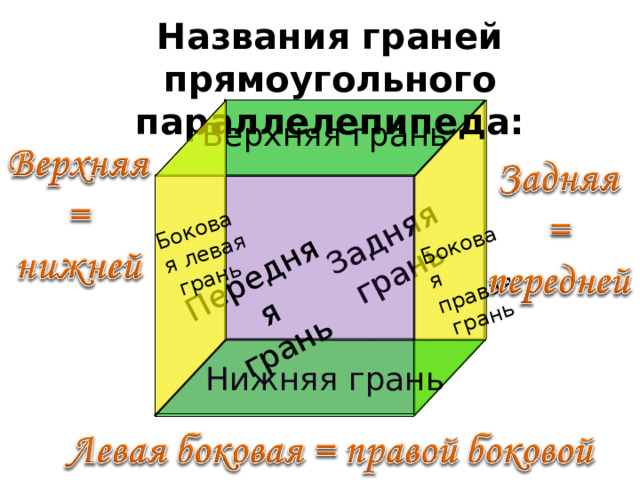
Задняя
грань
Боковая правая
грань
Передняя
грань
Боковая левая
грань
Названия граней прямоугольного параллелепипеда:
Верхняя грань
Нижняя грань
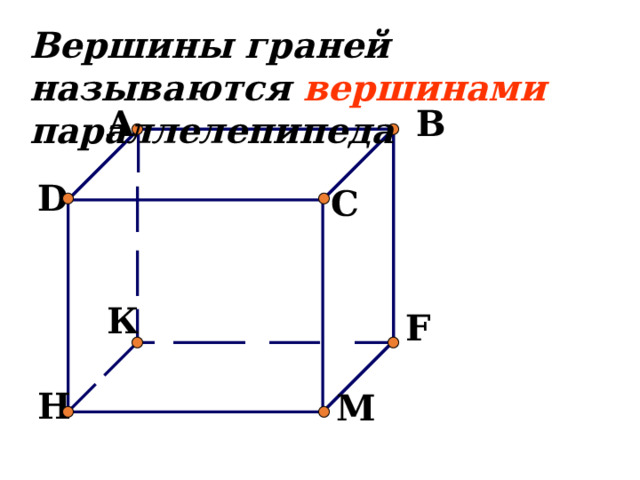
Вершины граней называются вершинами параллелепипеда
A
B
D
C
К
F
H
М
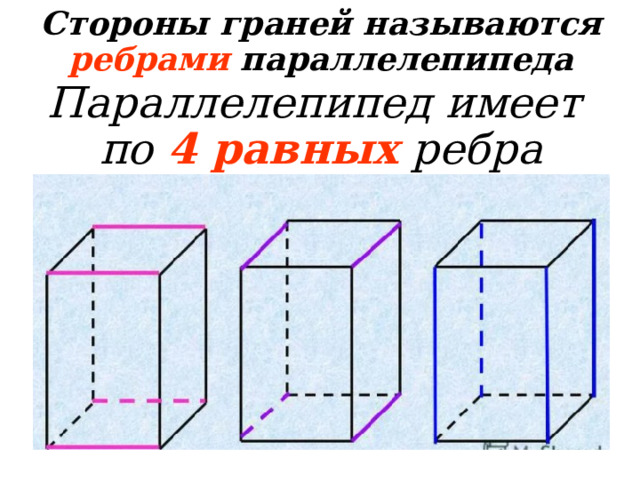
Стороны граней называются ребрами параллелепипеда
Параллелепипед имеет по 4 равных ребра
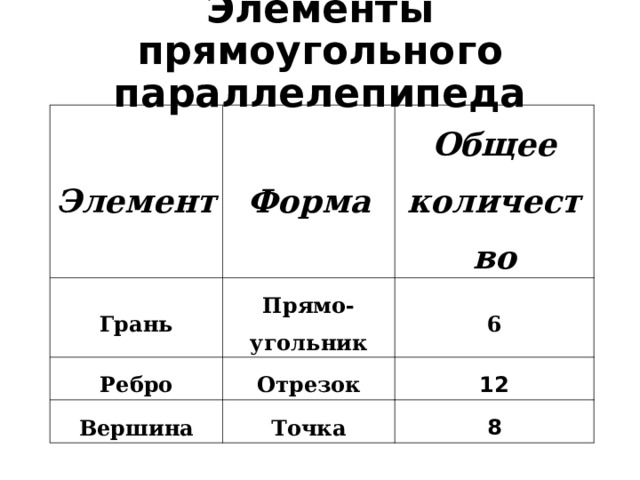
Элементы прямоугольного параллелепипеда
Элемент
Форма
Грань
Общее количество
Прямо-угольник
Ребро
Отрезок
6
Вершина
12
Точка
8
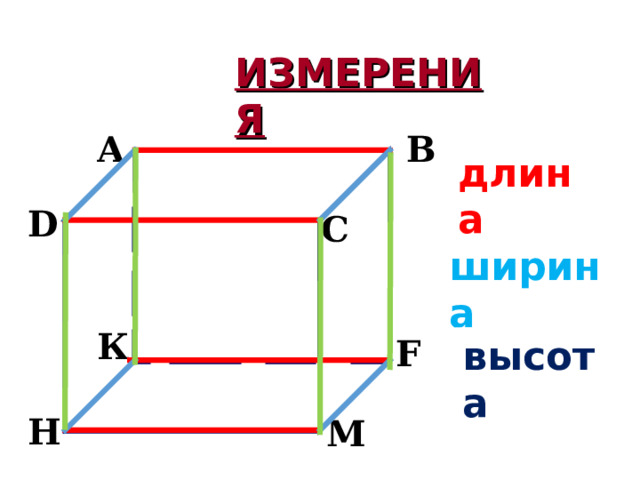
ИЗМЕРЕНИЯ
B
A
длина
D
C
ширина
К
F
высота
H
М
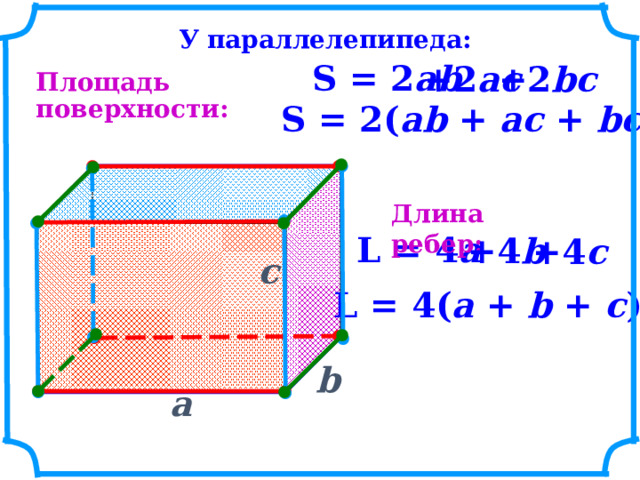
У параллелепипеда:
S = 2 ab
+ 2 bc
+2 ac
Площадь поверхности:
S = 2( ab + ac + bc )
Длина ребер:
L = 4 a
+4 b
+4 c
c
L = 4( a + b + c )
b
a
17
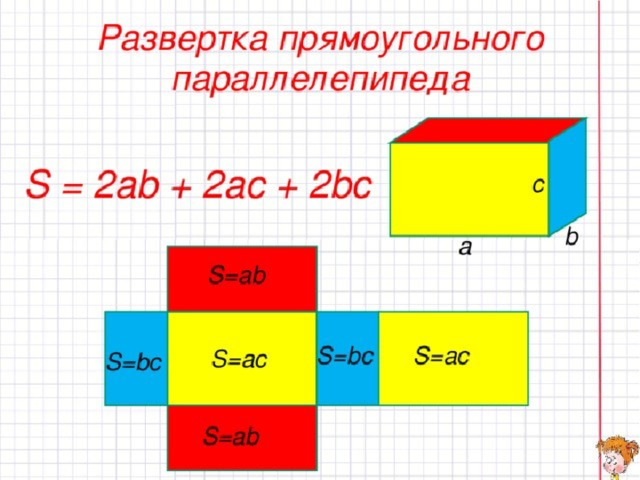
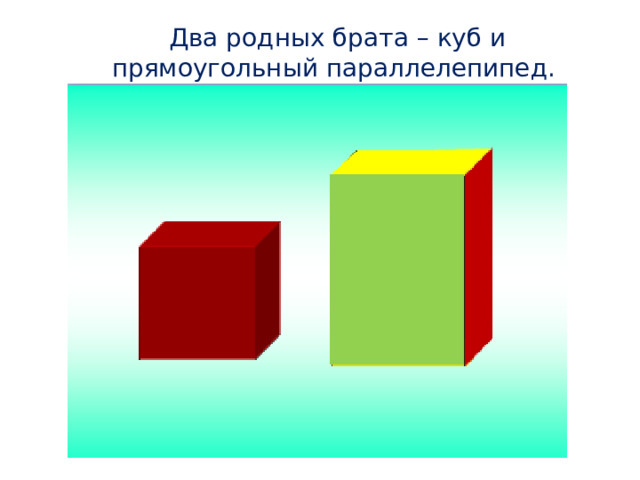
Два родных брата – куб и прямоугольный параллелепипед.
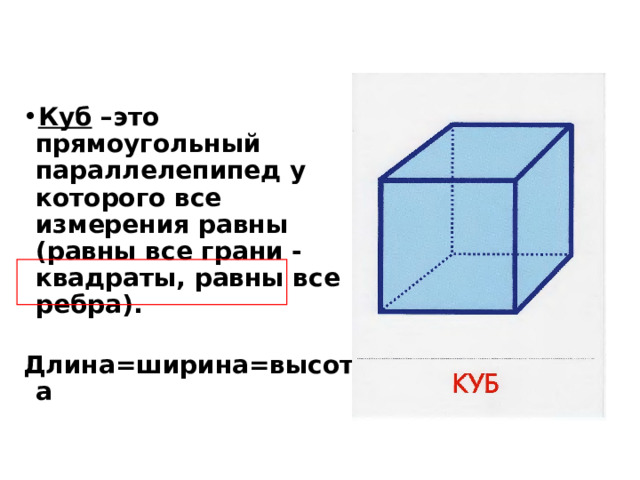
- Куб –это прямоугольный параллелепипед у которого все измерения равны (равны все грани - квадраты, равны все ребра).
Длина=ширина=высота
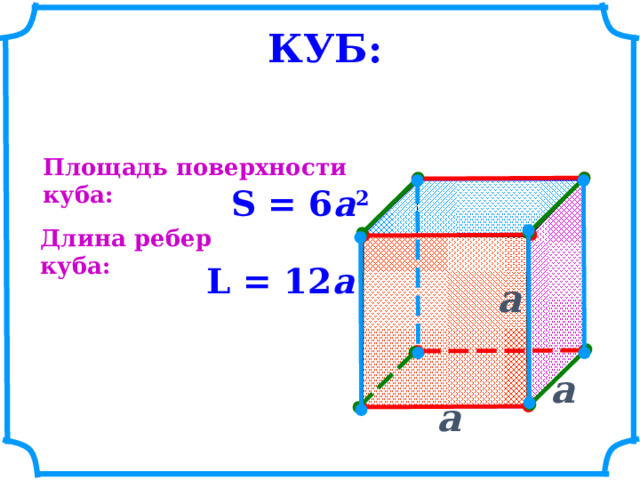
КУБ:
Площадь поверхности куба:
S = 6 a 2
Длина ребер куба:
L = 12 a
a
a
a

В ы в о д ы : прямоугольный параллелепипед имеет:
6 граней 12 рёбер 8 вершин
Грани: прямоугольники, квадраты
S поверхности = 2(ав +ас +вс)
L=4 а + 4в + 4с
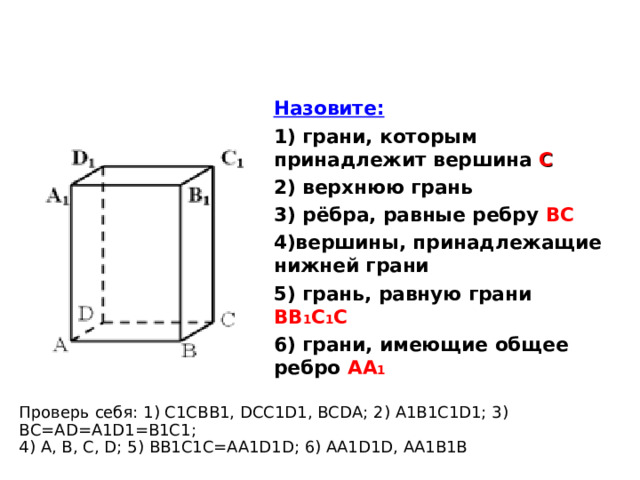
Назовите:
1) грани, которым принадлежит вершина С
2) верхнюю грань
3) рёбра, равные ребру ВС
4)вершины, принадлежащие нижней грани
5) грань, равную грани ВВ 1 С 1 С
6) грани, имеющие общее ребро АА 1
Проверь себя: 1) С1С BB1 , DCC1D1, BCDA ; 2) A1B1C1D1 ; 3) BC=AD=A1D1=B1C1 ; 4) A, B, C, D ; 5) BB1C1C=AA1D1D ; 6) AA1D1D, AA1B1B
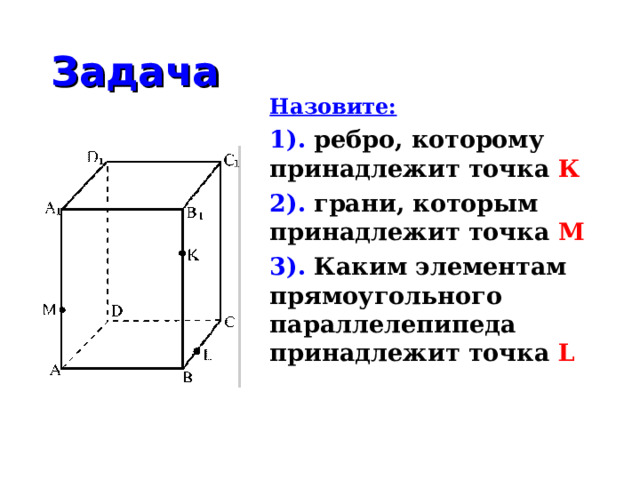
Задача
Назовите:
1). ребро, которому принадлежит точка К
2). грани, которым принадлежит точка М
3). Каким элементам прямоугольного параллелепипеда принадлежит точка L
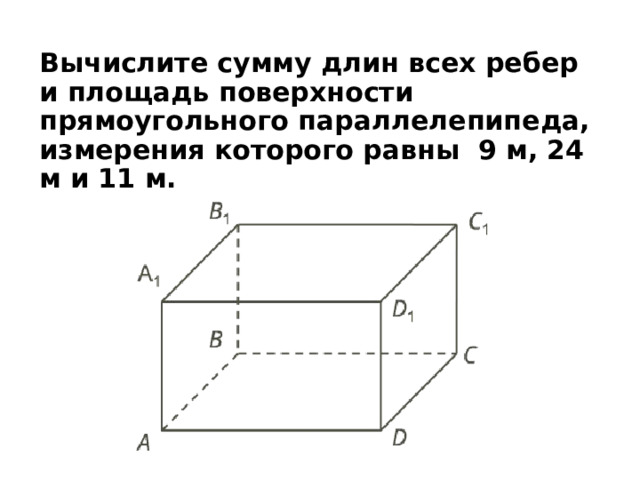
Вычислите сумму длин всех ребер и площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м и 11 м.
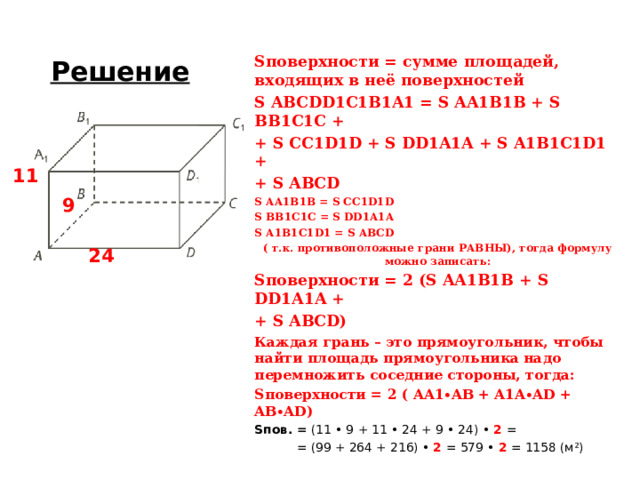
Решение
S поверхности = сумме площадей, входящих в неё поверхностей
S ABCDD1C1B1A1 = S AA1B1B + S BB1C1C +
+ S CC1D1D + S DD1A1A + S A1B1C1D1 +
+ S ABCD
S AA1B1B = S CC1D1D
S BB1C1C = S DD1A1A
S A1B1C1D1 = S ABCD
( т.к. противоположные грани РАВНЫ), тогда формулу можно записать:
S поверхности = 2 ( S AA1B1B + S DD1A1A +
+ S ABCD )
Каждая грань – это прямоугольник, чтобы найти площадь прямоугольника надо перемножить соседние стороны, тогда:
S поверхности = 2 ( AA1∙AB + A1A∙AD + AB∙AD )
S пов. = (11 • 9 + 11 • 24 + 9 • 24) • 2 =
= (99 + 264 + 216) • 2 = 579 • 2 = 1158 (м ² )
11
9
24
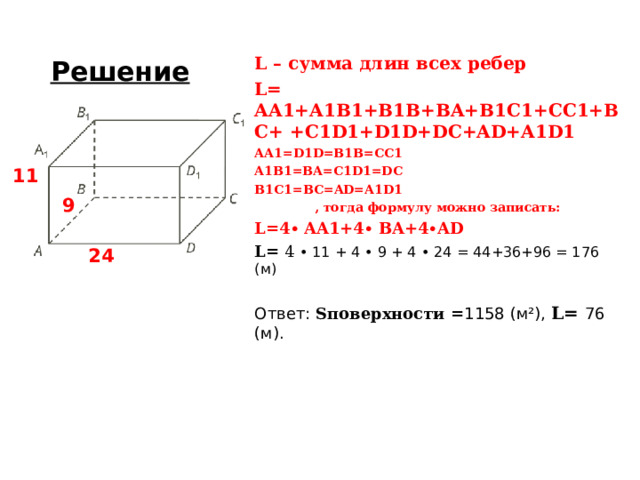
Решение
L – сумма длин всех ребер
L = AA1+A1B1+B1B+BA+B1C1+CC1+BC+ +C1D1+D1D+DC+AD+A1D1
AA1 = D1D = B1B = CC1
A1B1 = BA = C1D1 = DC
B1C1 = BC = AD=A1D1
, тогда формулу можно записать:
L=4∙ AA1+4∙ BA+4∙AD
L = 4 • 11 + 4 • 9 + 4 • 24 = 44+36+96 = 176 (м)
Ответ: S поверхности = 1158 (м ² ), L = 76 (м).
11
9
24
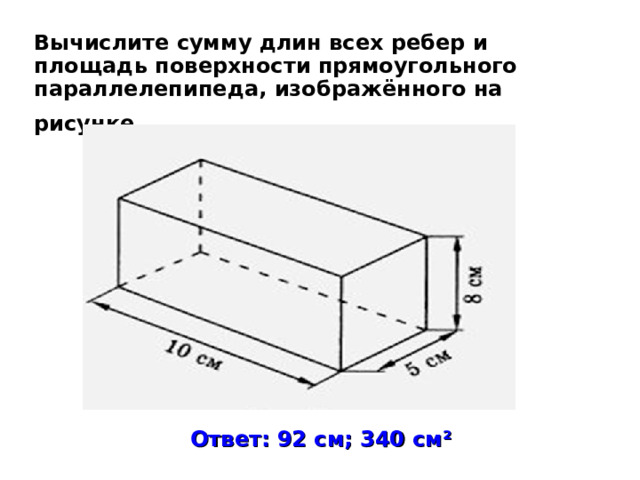
Вычислите сумму длин всех ребер и площадь поверхности прямоугольного параллелепипеда, изображённого на рисунке.
Ответ: 92 см; 340 см ²
















































