Представление числовой информации с помощью систем счисления

Тема урока: Представление числовой информации с помощью систем счисления.

Цель

• Рассказать о системах счисления. Дать представление о позиционной и непозиционной системах счисления. Научить представлять числа в разных системах счисления.

Тип урока: изучение нового материала

Ход урока

1. Организационный момент

2. Актуализация опорных знаний

Фронтальный опрос:

1. Какие существуют языки предоставления информации?

2. Что такое информация?

3. Что такое кодирование? Декодирование? Шифрование? Код?

1. Изучение нового материала

Системы счисления

В процессе эволюции человек использовал самые разные системы счисления (восьмеричная, шестнадцатеричная и т.д), но наиболее удобной на практике оказалась именно десятеричная система.

Наверное, это было как-то связано с физиологией человеческого тела – у него человека на руках и ногах по десять пальцев.

Но не будем спешить - ведь не все же системы используют такое счисление.

Например, электронные вычислительные машины чрезвычайно эффективно используют двоичную систему счисления, в которой используются лишь две цифры - это 0 и 1.

Причина проста – ведь с точки зрения техники машину с двумя состояниями проще создать, причем упрощаются различения этих состояний.

Совокупность методов и приёмов для записи чисел цифровыми знаками называют системой счисления.

Они разделяются на позиционные и непозиционные.

В позиционной системе счисления используются число в определённом порядке для обозначения каких-либо чисел, а значение каждого символа зависит расположения этого символа по отношению к другим в том же числе. Пример - арабская десятичная система счисления.

В непозиционной системе все наоборот - значение каждого символа не зависит от его расположения по отношению к другим в том же числе.

Двоичная система счисления

И так, как уже было сказано, для компьютера самая подходящая система счисления – двоичная. В такой системе используются лишь два символа - 0 и 1.

И этот метод отлично «дружит» с техническими данными различных цифровых схем. Оказалось, что представлять разные составляющие информации двумя состояниями очень удобно:

• Тело намагничено или размагничено (дискеты, жесткие диски магнитные ленты)

• Отверстие есть или нет (перфокарта)

• Уровень сигнала большой или маленький

• Черный цвет или белый

Для отображения таких состояний в цифровых системах нужно иметь электросхемы, принимающие два состояния и четко различающие значения электрической величины - потенциала или тока. Каждому из таких значений соответствует или 0 или 1 (обычно «0» представляет низкий уровень потенциала, а «1» – высокий).

Простота создания электросхем с двумя электрическими состояниями и есть причиной того, что двоичное представление чисел «лидирует» в мире современной цифровой техники.

Также существуют термины, широко используемые в вычислительной сфере - бит, байт, слово.

Бит – это один двоичный разряд. Крайний слева бит числа - старший разряд (наибольший вес), крайний справа – младший (наименьший вес).

Восьмибитовая единица есть байт.

Современные компьютеры перерабатывают информацию порциями (словами) по 8, 16 или 32 бита (1, 2 и 4 байта) и т.д.

Перевод чисел из одной системы счисления в другую

При переводе чисел, например, из десятичной системы в двоичную, используется метод деления в столбик. Попробуем проделать такую операцию с числом 567.

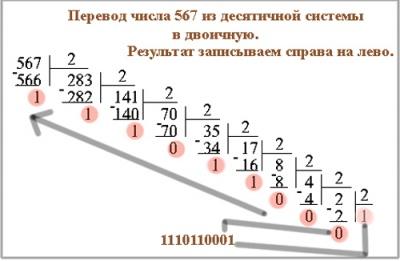
При деление 567 на 2 выходит целое 283 и остаток 1.

Проведем то же действие с числом 283 - целое 141, остаток 1.

Снова делим полученное целое число на 2 - и так до тех пор, пока целое число не станет меньше делителя.

А для того, чтобы получить число в двоичной системе счисления, нужно записать последнее целое число (в нашем случае это 1) и приписать к нему все полученные в во время деления остатки в обратном порядке.

Выходит, что число в десятеричной системе счисления 567 будет, выглядит в двоичной как 1000110111.

А теперь, попробуем перевести из двоичной системы в десятеричную: 10110110₂ = (1·2⁷)+(0·2⁶)+(1·2⁵)+(1·2⁴)+(0·2³)+(1·2²)+(1·2¹)+(0·2⁰) = 128+32+16+4+2 = 182₁₀

1. Систематизация полученных знаний

Самостоятельная работа

1. Перевести из десятеричной системы в двоичную:

23, 54, 789, 3456, 6578, 891234

1. Перевести из двоичной системы в десятеричную систему.

1000111_2, 1000001_2, 111010000₂

Ответы: 71, 65, 464

1. Итог урока

Вопросы

1. Что такое система счисления?

2. Позиционные и непозиционные системы счисления.

3. Что представляет собой двоичная система счисления?

4. Как можно перевести число из десятичной системы в двоичную?

VI. Домашнее задание

Решить задания №9, 10 стр. 204

Учить определения