Представление числовой информации с помощью систем счисления

Системы

счисления

«Всё есть число»

Так говорили древние пифагорейцы.

Что они имели в виду?

Этой фразой пифагорейцы подчеркивали необычайно важную роль чисел в практической деятельности.

Пифагор

Цифры

– это символы, участвующие в записи числа и составляющие некоторый алфавит.

Число

– это некоторая величина.

– это способ записи чисел с помощью цифр.

Система счисления

Системы счисления

Непозиционные

Позиционные

- системы счисления, у которых количественный эквивалент цифры не зависит от её местоположения в записи числа.

• системы счисления, у которых количественный эквивалент цифры зависит от её местоположения в записи числа.

XXX = 10 + 10 + 10

333 = 300 + 30 + 3

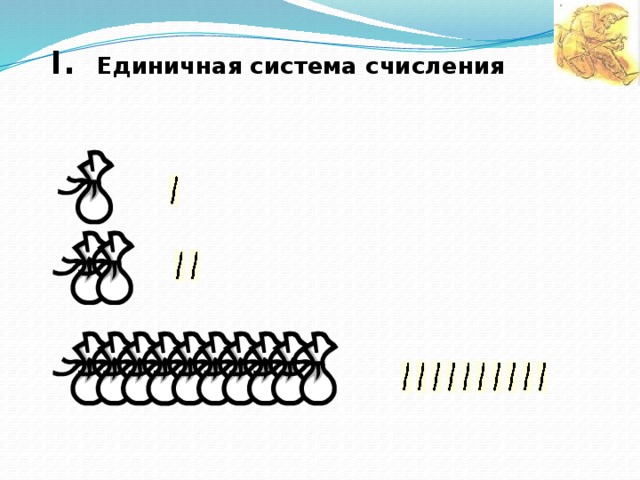
I. Единичная система счисления

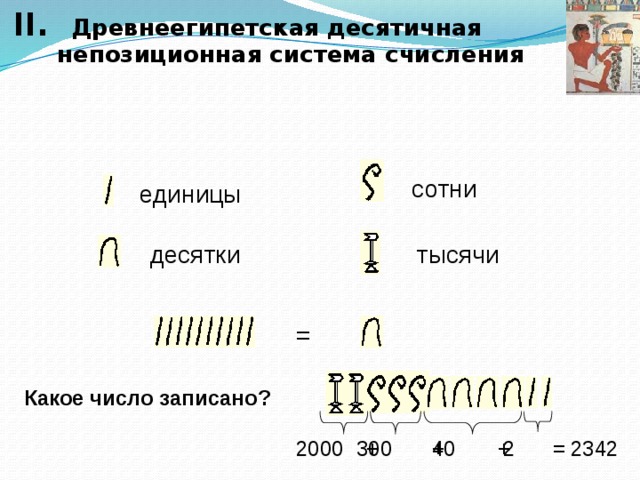
II. Древнеегипетская десятичная непозиционная система счисления

сотни

единицы

десятки

тысячи

=

Какое число записано?

300

40

2

2000

+

+

+

=

2342

III. Римская система счисления

I – 1, V – 5, X – 10, L – 50,

C – 100, D – 500, M - 1000

Правила составления чисел в римской системе счисления:

Величина числа определяется как сумма или разность цифр в числе.

Если меньшая цифра стоит слева от большей, то она вычитается .

IV = V – I IX = X – I XL = L – X XC = C - X

Если меньшая цифра стоит справа от большей, то она прибавляется .

VI = V + I XI = X + I LX = L + X CX = C + X

III. Римская система счисления

I – 1, V – 5, X – 10, L – 50,

C – 100, D – 500, M - 1000

444

400 + 40 + 4

(D – C)

(V – I)

(L – X)

CD

XL

IV

III. Римская система счисления

I – 1, V – 5, X – 10, L – 50,

C – 100, D – 500, M - 1000

Какие числа записаны с помощью римских цифр?

MMIV

= 2004

LXV

= 65

CMLXIV

= 964

Выполните действия:

MMMD + LX

= 3560

IV. Греческая система счисления

- 1

I

I, II, III, IIII - 1, 2, 3, 4

- 5

Γ

- 10

Δ

Какое число записано?

- 100

Η

Δ Δ Δ I I I I

- 1000

Χ

- 10 000

Μ

10+10+10 + 4

=

34

V. Алфавитные системы

1

а

2

в

Аз

3

10

Веди

4

г

20

д

ι

Глаголь

5

є

Добро

6

30

И

к

Како

40

ѕ

Есть

100

7

л

200

z

50

р

Зело

8

м

Люди

с

н

Мыслете

60

9

Земля

300

N

70

Иже

400

т

Наш

ξ

θ

у

80

Кси

о

500

Фита

90

ф

Он

600

п

Покой

х

џ

700

Червь

800

ψ

ω

900

ц

- титло

Какое число записано в славянской системе счисления?

= 23

= 444

V. Алфавитные системы

1

а

2

в

Аз

3

4

10

г

Веди

20

д

5

ι

Глаголь

к

6

є

И

30

Добро

40

ѕ

Како

Есть

100

л

7

Зело

р

8

50

z

200

м

Люди

с

н

Мыслете

60

9

300

Земля

N

Иже

θ

70

т

ξ

Наш

400

у

Кси

80

о

500

Фита

90

Он

600

ф

п

х

Покой

700

џ

800

ψ

Червь

ω

900

ц

1000 =

3000 =

2000 =

40 000 =

30 000 =

20 000 =

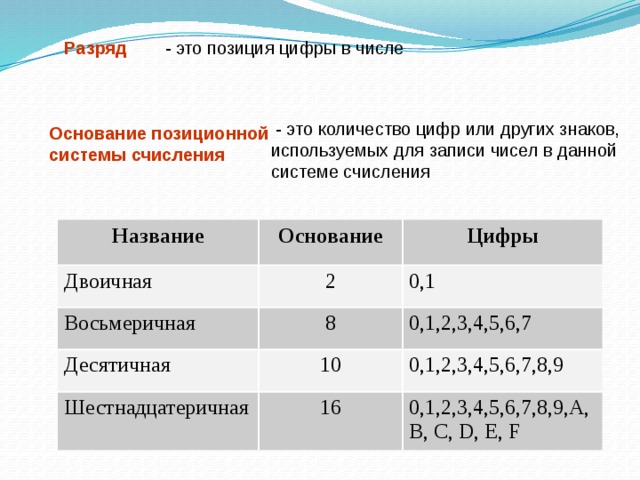
Разряд

- это позиция цифры в числе

- это количество цифр или других знаков, используемых для записи чисел в данной системе счисления

Основание позиционной системы счисления

Название

Двоичная

Основание

Цифры

2

Восьмеричная

Десятичная

0,1

8

Шестнадцатеричная

0,1,2,3,4,5,6,7

10

0,1,2,3,4,5,6,7,8,9

16

0,1,2,3,4,5,6,7,8,9,А, B, C, D, E, F

В позиционной системе счисления любое вещественное число может быть представлено в виде:

A q =

(a n-1 q n-1 +a n-2 q n-2 +…a 0 q 0 +a -1 q -1 +a -2 q -2 +…a -m q -m )

- развернутая форма записи числа

Здесь:

A – само число

q – основание системы счисления

a i – цифры данной системы счисления

n – число разрядов целой части числа

m – число разрядов дробной части числа

Как будет выглядеть в развернутом виде число А 10 = 4718,63 ?

n = 4

q = 10

m = 2

А 10 =

4 ·10 3

+ 7 · 10 2

+ 1 ·10 1

+ 8 ·10 0

+ 6 ·10 -1

+ 3 ·10 -2

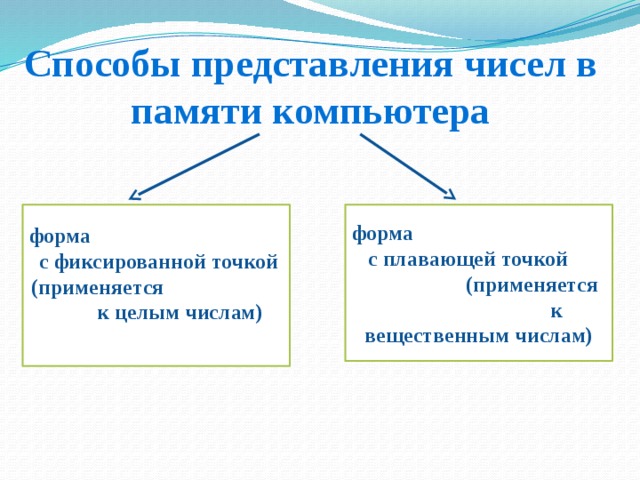
Способы представления чисел в памяти компьютера

форма с фиксированной точкой (применяется к целым числам)

форма с плавающей точкой (применяется к вещественным числам)

Главные правила представления данных в компьютере

Правило № 1

Данные (и программы) в памяти компьютера хранятся в двоичном виде, т.е. в виде цепочек единиц и нулей.

Правило № 2

Представление данных в компьютер дискретно.

Дискретизация  — преобразование непрерывной функции в дискретную.

Правило № 3

Множество представленных в памяти величин ограничено и конечно.

Целые числа в компьютере

Правило № 4

В памяти компьютера числа хранятся в двоичной системе счисления.

Вывод:

Целые числа в памяти компьютера – это дискретное, ограниченное и конечное множество.

Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака.

Перевод из двоичной системы в десятичную

• 10110110 2 = (1·2 7 )+(0·2 6 )+(1·2 5 )+(1·2 4 )+(0·2 3 )+(1·2 2 )+(1·2 1 )+(0·2 0 ) = 128+32+16+4+2 = 182 10

Самостоятельная работа

Запишите в римской системе счисления числа:

1. 9 =

12 =

2778 =

2. Какие числа записаны с помощью римских цифр:

LXV=

MCMLXXXVI =

Исправьте неверные равенства, переложив с одного места на другое только одну палочку:

VII –V = XI

IX – V = VI

• Перевести из десятеричной системы в двоичную:

23, 54, 789, 3456, 6578, 891234

• Перевести из двоичной системы в десятеричную систему.

1000111 2, 1000001 2, 111010000 2

Домашнее задание

• Решить задания №9, 10 стр. 204
• Учить определения