2.3. ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ФОРМУЛЬНОМ ВИДЕ
ПОНЯТЬ
Подумайте и назовите те школьные предметы, при изучении которых вам встречались формулы. Вероятно, в первую очередь вы вспомнили об арифметике, алгебре, геометрии, физике. Формулы, которые там встречаются, называются математическими формулами. Они используются для обозначения самой различной информации: условий математических задач, физических законов, закономерностей развития физических, экономических, социальных систем и пр.
В математике формула (от лат. formula - форма, правило, предписание) определяется как комбинация математических знаков, выражающая какое-либо предложение.
Например, следующие выражения суть формулы:
2 х 2 = 4
x3 + z2
DABC ~ DEFG
(A Щ B) Ю C = Ш AЪШ BЪ C
2 х 2 = 5
y’ = y
Словом “математические” подчеркивается, что все знаки в этих формулах наполняются смыслом, принятым в математике, рассматриваются как математические объекты. То есть “+” рассматривается как обозначение арифметической операции сложения или принадлежности числа к множеству положительных чисел, “=” - как равенство, совпадение числовых значений выражений, стоящих по разные стороны от данного знака и т.д.
ПРИМЕР 1
Бином Ньютона для n=3 записывается так: (1+х)3 = 1+3х+3х2+х3
Длина окружности радиуса r: c = 2pr
Закон Ома: I = U / R, где R - сопротивление проводника, U - напряжение на его концах, I - сила тока.
В экономике, статистике для описания процессов и явлений тоже чаще всего используются математические формулы.
ПРИМЕР 2
Для определения, какова будет величина вклада в S рублей через N лет, положенного в банк под Р% годовых, если начисление производится m раз в год, следует воспользоваться формулой:
BS = S (1 + P / m / 100)N m
Чтобы вычислить среднемесячную прибыль предприятия за первое полугодие 2000 года, потребуется провести расчет по формуле:
SP = S Pk / 6,
где kО [1,6]- номер месяца, Pk - прибыль в k-ом месяце
Кроме математических, вам известны химические формулы: формулы веществ и формулы химических реакций. В них знак “+” имеет смысл, например, химического взаимодействия веществ, а знак “=” показывает, что далее записывается результат этого взаимодействия.
ПРИМЕР 3
При взаимодействии гидроксида натрия с соляной кислотой образуется хлористый натрий и вода. Записывается это так:
HCl + NaOH = NaCl + H2O
Реакции подобного вида называются ионными реакциями. Иногда их записывают с помощью сокращенных ионных уравнений, показывающих, какие ионы реагируют друг с другом. Сокращенным ионным уравнением в этом случае будет:
H+ + OH- = H2O
Заметим, что в этой формуле один и тот же знак “+” имеет разный смысл и используется для обозначения “положительности” иона водорода и для обозначения соединения двух ионов.
С формулами вы можете встретиться и при изучении таких “чисто гуманитарных” наук, как литературоведение, история, логика, психология.
ПРИМЕР 4
В психологии хорошо известна формула определения самооценки личности (Джемс, 1890):
САМООЦЕНКА = УСПЕХ / ПРИТЯЗАНИЯ
Знак деления не означает здесь деления в арифметическом смысле. По сути операция деления используется здесь как модель отношения между тремя взаимосвязанными объектами.
Проанализируйте эту формулу и вы увидите, что фактически Джемс указал на два пути повышения самооценки. В самом деле, человек может улучшить представление о себе либо увеличивая числитель дроби, либо уменьшая знаменатель, поскольку для самооценки важно лишь соотношение этих показателей. Как мудро заметил Джемс, “наше самоощущение в этом мире зависит исключительно от того, кем мы вознамерились стать и что мы вознамерились совершить”.
ОСНОВНОЕ ОТЛИЧИЕ ФОРМУЛ состоит в том, что информация представлена в них в наиболее “свернутом”, наиболее компактном виде. В формулах практически нет избыточности информации - не только каждый знак, но и их взаимное расположение несет важную смысловую нагрузку (а2 и а2 - имеют разный смысл). Именно поэтому воспринимать “незнакомые” формулы тяжело - их приходится обязательно “расшифровывать”, переводить на более привычный для вас язык. Но и описание какого-либо объекта с помощью формул требует определенных знаний и умений, в частности, умений анализировать, сравнивать, сопоставлять, обобщать информацию, видеть закономерности за разрозненными фактами.
Основные этапы построения математических формул и некоторые их свойства рассмотрим на следующих примерах.
ПРИМЕР 5
Моделью соотношения сторон прямоугольного треугольника является, например, теорема пифагора: квадрат гипотенузы равен сумме квадратов катетов. Где катетами называются стороны, прилежащие прямому углу треугольника, гипотенузой - сторона, противолежащая прямому углу.
Чтобы представить эту модель в формульном виде, следует:
выделить существенные элементы, описанные в теореме (задаче);
обозначить их (исторически принято обозначать латинскими или греческими буквами, поскольку латынь всегда рассматривалась как язык науки, а ученые древней греции считаются основателями европейской математики);
установить, в каком отношении находятся выделенные элементы и какие математические операции соответствуют этим отношениям;
записать с использованием введенных обозначений и математической символики (знаков математических операций) соотношения между выделенными существенными элементами.
Итак, элементами прямоугольного треугольника, о котором идет речь в теореме, являются стороны (катеты и гипотенуза) треугольника и их длины, углы треугольника и величины этих углов. Существенными элементами с точки зрения формулировки теоремы являются длины катетов и длина гипотенузы.
Общепринято обозначать длины катетов буквами a и b, длину гипотенузы - буквай с. Под a, b и с подразумеваются некоторые числовые значения, которые можно перемножать сами на себя (возводить в квадрат) и сравнивать между собой.
В этих обозначениях теорема записывается так:
a2 + b2 = c2
Заметим, что запись вида а2 сама является моделью произведения двух одинаковых чисел а. То есть теорему Пифагора можно записать и так: a*a+b*b=c*c.
А если обозначить катеты буквами g и r, а гипотенузу буквой q, то формула теоремы Пифагора будет имет совсем непривычный вид: g2 + r2 = q2 , но нести она будет то же самое содержание.
Мы выбрали эту известную вам формулу в качестве примера, но смысл и порядок построения модели в формульном виде она передает достаточно точно.
Кроме математического моделирования, как уже сказано выше, формулы встречаются также в химии, лингвистике, литературоведении, логике, хотя основными видами инфомационного моделирования в них являются словесное описание, рисунки, схемы, таблицы, алгоритмы. Но коль используются формулы, следовательно, есть и соответствующие приемы формализации.
ПРИМЕР 6
Существует, например, такой способ формализации при построении формул химических соединений.
1. Написать в ряд химические знаки элементов, входящих в состав соединения:
Al O Na O
2. Над знаками элементов поставить их валентность в соответствии с таблицей периодической системы элементов Д.И.Менделеева:
III II I II
Al O Na O
3. Определить наименьшее кратное этих чисел:
(6) (2)
III II I II
Al O Na O
4. Делением наименьшего общего кратного на валентность соответствующего элемента определить индексы:
(6) (2)
III II I II
Al2 O3 Na2 О
Для чего же нужны формулы?
Одной из важнейших задач познания есть установление причинно-следственных связей. Наиболее точным формальным воплощением этих связей является функциональная зависимость. Наиболее компактно она выражается на языке формул.
ПРИМЕР 7
Пусть длина катета а прямугольного треугольника является переменной величиной и может принимать любое значение из интервала [t1, t2]. Тогда, если длина второго катета величина постоянная, то длина гипотенузы с есть функция от длины катета а.
с(а) = Ц а2 + b2, для а О [t1, t2].
В этом случае длина гипотенузы с зависит от длины катета а. Это значит, что между ними существует причинно-следственная связь и формула хорошо отражает эту связь. Эту зависимость можно отразить и с помощью таблиц, но лишь частично:
| Длина катета а | Длина гипотенузы с при b = 3 |
| 1 | 3,16 |
| 4 | 5 |
| 7 | 7,62 |
| 10 | 10,44 |
Заметим, что математические модели в физике служат как раз для установления причинно-следственных связей физических явлений и предсказания поведения физических объектов (выведение следствий), если известно, какое воздействие оказывается на эти объекты (известная причина).
ПРИМЕР 8
Определить, на какой высоте через t секунд будет мячик, брошенный вертикально вверх со скоростью v м/сек, если сопротивлением воздуха можно пренебречь, позволяет формула:
h = vt-gt2/2
Узнать, с какой скоростью полетят шары массами m1 и m2 после упругого столкновения, если до столкновения их скорости были v1 и v2 можно если воспользоваться формульным выражением закона сохранения импульса.
ПРИМЕР 9
Вновь рассмотрим некоторый треугольник. Как известно, для него справедливо утверждение: длина стороны треугольника не больше суммы двух других сторон. Формульная запись этого утверждения такова:
а
Здесь нет такой явно выраженной причинно-следственной связи. Эти три формулы выражают отношения, существующие между сторонами любого треугольника.
Повторим еще раз, что формула - наиболее сжатый, емкий способ представления информации. В ней практически нет избыточности информации, как, например, в словесных описаниях или таблицах. С другой стороны, формулы позволяют передать такие свойства объекта, которые не поддаются описанию другими средствами, например, свойство бесконечности.
ПРИМЕР 10
Функция может быть задана таблицей, графиком и формулой. Рассмотрим функцию y=(x+2)2-3.

| x | y |
| -5 | 6 |
| -4 | 1 |
| -3 | -2 |
| -2 | -3 |
| -1 | -2 |
| 0 | 1 |
| 1 | 6 |
| 2 | 13 |
| 3 | 22 |
| 4 | 33 |
| 5 | 46 |
Рис.2.3.1. График функции и ее табличное задание
В таблице можно передать только конечное число значений. График функции дает представление о ее поведении в ограниченной области. Формульное задание функции свободно от этих недостатков. Вы можете мыслить х (и, соответственно, у) любым сколь угодно большим или сколь угодно малым.
Со временем было осознано, что не для всех явлений в мире можно найти причинно-следственную связь, но мысль о том, что формула является очень удобным инструментом описания осталась. Поэтому со временем появились формулы, выражающие не только функциональную зависимость, но и различные недетерминированные процессы.
Математические формулы возникают, как правило, как результат исследования реальных физических, экономических, социальных систем. Основное их назначение в этом случае - предсказание свойств и поведения этих систем за пределами видимых наблюдений.
Ученые-математики вот уже несколько тысячелетий разрабатывают методы математического моделирования. Разработано много подходов, способов, рекомендаций по исследованию систем и построению их математических моделей. О математическом моделировании физических, социальных явлений, производственных процессов и т.п. вы многое узнаете на уроках математики, физики, информатики и в процессе получения высшего образования. Нередко математические модели будут встречаться и на страницах этой книги.
ЗНАТЬ
Формулы как вид информационного моделирования встречаются во многих областях знаний, прежде всего, математике, физике, химии, экономике, статистике, логике.
Основное отличие формул состоит в том, что информация представлена в них в наиболее “свернутом”, наиболее компактном виде. В формулах практически нет избыточности информаци - не только каждый знак, но и их взаимное расположение несет важную смысловую нагрузку.
Наиболее распространенным видом информационного моделирования в науке является математическое моделирование, а язык математики называют универсальным языком науки.
Математическая модель - приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики (Математический энциклопедический словарь / Гл. ред. Ю.В.Прохоров. М.: Сов. энциклопедия, 1988. 847с.)
Математические формулы возникают, как правило, как результат исследования реальных физических, экономических, социальных систем. Основное их назначение - описание наблюдаемого поведения систем и предсказание свойств и поведения этих систем за пределами видимых наблюдений.
Укрупненные этапы построения математической модели:
выделить существенные элементы, описанные в теореме (задаче);
обозначить их (исторически принято обозначать латинскими или греческими буквами, поскольку латынь всегда рассматривалась как язык науки, а ученые древней греции считаются основателями европейской математики);
установить, в каком отношении находятся выделенные элементы и какие математические операции соответствуют этим отношениям;
записать с использованием введенных обозначений и математической символики (знаков математических операций) соотношения между выделенными существенными элементами.
Использование формул позволяет:
давать описание объекта в наиболее компактном виде;
отразить причинно-следственные связи физических явлений;
передать такие свойства объекта, которые не поддаются описанию другими средствами, например, свойство бесконечности;
предсказать свойства и поведение моделируемого объекта за пределами видимых наблюдений.
Математическое моделирование - мощный метод познания внешнего мира, прогнозирования и управления.
Анализ математических моделей позволяет проникнуть в сущность изучаемых явлений. Это обуславливает широкое распространение данного вида моделирования в науке и в практической деятельности и особую роль математических моделей в классе информационных моделей.
УМЕТЬ
ЗАДАНИЕ 1
Постройте математическую модель для решения следующей задачи и опишите этапы формализации ее условия.
Цена товара была дважды повышена на одно и то же число процентов. На сколько процентов повышалась цена товара каждый раз, если его первоначальная стоимость 6000 руб., а окончательная 6615 руб.?
ОТВЕТ
Элементами, о которых идет речь в условии являются: первоначальная цена (обозначим ее СР), процент повышения (Р), окончательная цена (СО). Между ними существует связь, которую с помощью математической символики можно записать так: СО = СР(1+P/100)2
ЗАДАНИЕ 2
Предыдущая задача взята из учебника алгебры для 9 класса, следующая - из рабочей тетради по математике для 2 класса. Попробуйте построить математическую модель для нее.
Возраст старика Хоттабыча записывается числом с разными цифрами. Известно, что:
а) если первую и последнюю цифру зачеркнуть, то получится наибольшее из двузначных чисел, сумма цифр которых равна 13;
б) первая цифра больше последней в четыре раза.
Сколько лет Хоттабычу?
ОТВЕТ: 8942 года.
Z = abcd, где 0
a=4d
b+c=13, bc = max xy, таких, что x+y=13
ЗАДАНИЕ 3
Выделите и опишите этапы формализации при решении задач из курса физики. Например, для следующей задачи.
Спортсмен во время прыжков преодолел высоту 2 м, после чего поднялся по ступенькам трибуны на высоту 2 м. Одинаковые ли мощности он развивал при этом?
ОТВЕТ
По условиям задачи необходимо выяснить, в каком отношении находятся между собой высота и мощность. Но для решения задачи важно, что неявно подразумевается еще и время подъема на заданную высоту.
Существенными свойствами для решения задачи будут такие физические характеристики, как:
а) работа и время ее совершения для определения мощности по формуле P = A / t
б) сила, приложенная к телу и пройденный путь для определения работы A = F s
в) масса тела и его ускорение для определения силы F = mg
Поскольку все величины, кроме времени подъема на заданную высоту, одинаковы в обоих случаях, то существенным свойством является только время подъема на заданную высоту и вид его связи с мощьностью. Поскольку зависимость между мощностью и временем обратно пропорциональная, то чем меньше время подъема, тем больше мощность. Следовательно мощность, развитая спортсменом во время прыжка, больше, чем та, которую он развил, поднимаясь по ступеням.
ЗАДАНИЕ 4
Выделите и опишите этапы формализации при построении формул химических реакций.
ЗАДАНИЕ 5
Возьмите какую-либо хорошо известную вам и вашим одноклассникам формулу из курса математики или физики. Измените в ней только обозначения и предложите одноклассникам “угадать”, какая это формула и какой объект она описывает.
ЗАДАНИЕ 6
Если вы уже изучили в курсе информатики или математики раздел, посвященный алгебре логики (иное название - булева алгебра), то формализуйте условия следующей задачи.
Перед тем, как A,B,C,D приняли участие в забеге, они сделали следующие предположения:
A предсказал победу B;
B предсказал, чтоD окажется на последнем месте;
C предсказал, что А займет третье место;
D предсказал, что прогноз A оправдается.
Только одно из сделанных предположений оказалось верным и это был прогноз победителя. В каком порядке A,B,C и D пересекли финишную черту?
ОТВЕТ
Введем следующие обозначения:
А - прогноз А оправдался;
 А - прогноз А не оправдался;
А - прогноз А не оправдался;
А1 - А занял первое место;
 А1 - А не занял первое место.
А1 - А не занял первое место.
Для всех остальных участников и занятых ими мест обозначения подобные.
Условие, что из всех сделанных предположений верным был только прогноз победителя, можно переформулировать так: победителем стал А и его прогноз верен, а прогнозы В, С, D неверные или победителем стал В и его прогноз верен, а прогнозы А, С, D неверные или и т.д. В виде формул алгебры логики это можно записать так:

Подставив вместо А, В, С и D их прогнозы, получим формулу, передающую условия задачи:
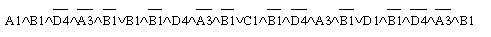
ЗАДАНИЕ 7
Приведите пример известной вам формулы из психологии, лингвистики, литературоведения или истории. Объясните смысл тех знаков, которые в нее входят, и смысл самой формулы.
ВОПРОСЫ-ПРОБЛЕМЫ
1. Являются ли график функции и табличное задание функции математическими моделями в соответствии с определением понятия “математическая модель”.
2. В логическом словаре ДЕФОРТ (ДЕдуктивная ФОРмализация Теорий) логическая формула определяется как переменная, построенная из некоторых других переменных и логических операторов. Справедливо ли данное определение для математических, химических, психологических и др. формул?
3. Иногда формализация определяется как процесс описания объекта исследования в виде, исключающем по возможности неоднозначное толкование данного объекта. Не противоречит ли это определение тому, что одна и та же математическая модель может описывать совершенно различные объекты?
РАСШИРЬ СВОЙ КРУГОЗОР
В програмировании формулы часто называют выражениями. В большинстве языков программирования они записываются максимально приближенно к их математической записи, но есть и особые правила. Например,
выражение может быть записано только в строку, никаких двухэтажных записей;
используются только круглые скобки;
знаки операций нельзя опускать;
для операции деления используется знак “/”, для умножения - “*”, для возведения в степень - “^” (если эта операция определена в языке);
аргументы функций обязательно заключаются в скобки.
Но арифметические операции записываются в привычном виде:
Например: Y:=(sqrt(x/2+5)-4*t-8)/x/t; как аналог математической формулы

Вместе с тем в программировании широкое распространение получила польская запись выражений перед их вычислением. Польской она называется поотому, что впервые была введена польским философом Я.Лукасевичем (1878-1956) в связи с формулами символической логики. Разновидностью польской записи является обратная польская запись, которая задается схемой:
ПРИМЕР
| Традиционная запись формулы | Обратная польская запись |
| AxB+CxD | ABxCDx+ |
| (A+B)xD | AB+Dx |
| A+(B+C)xD | ABC+Dx+ |
Иногда польскую запись называют бесскобочной записью. Это хороший пример специально созданного формального языка для записи формульных алгоритмов.
Особая форма записи формул в электронных таблицах. Например, формулу для вычисления суммы чисел, находящихся в ячейках А3, В3 и С3, в можно записать в Excel одним из следующих способов (все формулы в этом программном средстве начинаются со знака равенства):
=А3+В3+С3
=СУММ(А3:С3)
=СУММ(А3;В3;С3)

Рис. 2.3.3. Фрагмент электронной таблицы
Во многих современных электронных таблицах пользователю доступно много встроенных функций. Иногда одна функция заменяет сложную формулу. Так, расчитать будущую величину вклада в 1000 рублей, положенного на 5 лет под 15% годовых при начислении процентов один раз в год (см. пример 2 этого параграфа) в Excel, например, можно, используя финансовую функцию БЗ (Будущее Значение), задав формулу:
= БЗ (0,15; 5; ; 1000)
или так, как это показано на рис. 2.3.4.
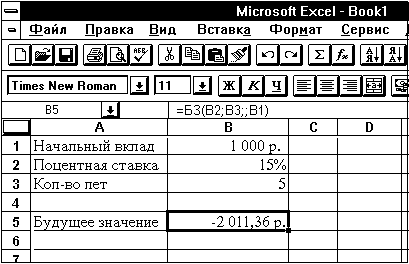
Рис. 2.3.4. Фрагмент электронной таблицы (формула видна в строке формул)
Интересно задание в Excel формул, в которые входят логические операции. Например, следующее условие: если содержимое ячейки А2 лежит в интервале от 5 до 20, то в текущую ячейку следует занести квадрат значения ячейки А1, в противном случае в текущую ячейку занести ноль, - можно записать следующей формулой:
=ЕСЛИ( И(А2=5; A2
Математическое моделирование является одним из основных методов системного анализа. Процесс математического моделирования при изучении явлений можно, по мнению академика А.Н.Тихонова, подразделить на четыре этапа.
Первый этап - формулирование законов, связывающих основные объекты модели. Этот этап требует широкого знания фактов, относящихся к изучаемым явлениям, и глубокого проникновения в их взаимосвязи. Эта стадия завершается записью в математических терминах представлений о связях между объектами модели. Нередко такую запись называют концептуальной моделью.
Второй этап - исследование математических задач, к которым приводит математическое моделирование. Основным вопросом здесь является получение в результате анализа модели выходных данных (теоретических следствий) для дальнейшего их сопоставления с результатами наблюдаений изучаемых явлений. На этом этапе важную роль приобретает математический аппарат, необходимый для анализа математической модели, и вычислительная техника - мощное средство для получения количественной выходной информации как результата решения сложных математических задач.
Третий этап - выяснение того, удовлетворяет ли принятая концептуальная модель критерию практики, то есть согласуются ли результаты наблюдений с теоретическими следствиями модели в пределах точности наблюдений.
Четвертый этап - последующий анализ модели в связи с накоплением данных об изучаемом явлении и модернизация модели. В процессе развития науки и техники данные об изучаемых явлениях все более и более уточняются и наступает момент, когда выводы, полученные на основании существующей модели, не соответствуют нашим знаниям о явлении. Таким образом, возникает необходимость построения новой, более совершенной (более адекватной) математической модели.








 А - прогноз А не оправдался;
А - прогноз А не оправдался; А1 - А не занял первое место.
А1 - А не занял первое место.











