Презентация " Движение в пространстве. Симметрия"

Движение пространства.

Симметрии.

Слайды 9,13,18

кликнуть на зелёный прямоугольник

Отображение пространства на себя.

Допустим, что каждой точке M пространства поставлена в соответствие некоторой точке M₁, причём любая точка M₁ пространства оказалась поставленной в соответствие какой-то точке M. Тогда говорят, что задано отображение пространства на себя.

Говорят также, что при данном отображении точка М переходит (отображается) в точку М₁.

M₁

.

M

.

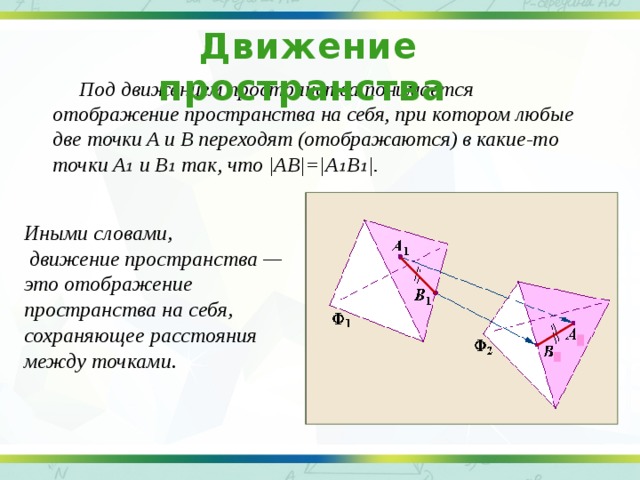
Движение пространства

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в какие-то точки A₁ и B₁ так, что |AB|=|A₁B₁|.

Иными словами,

движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками.

При движении в пространстве

  - прямые переходят в прямые,

- полупрямые — в полупрямые,

- отрезки — в отрезки,

- сохраняются углы между прямыми.

Новым свойством движения в пространстве является то,

что движение переводит плоскости в плоскости.

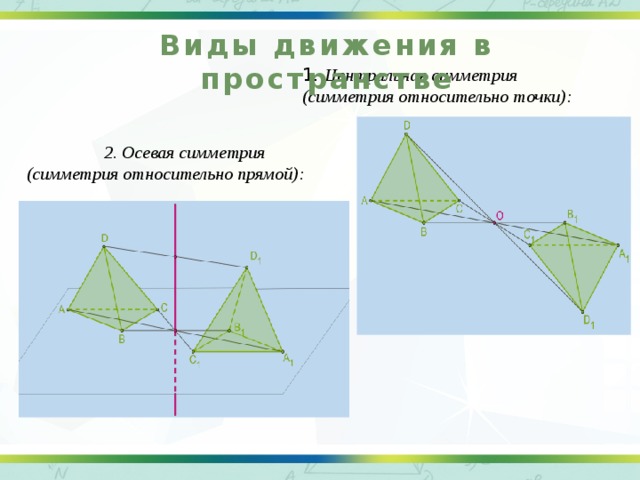
Виды движения в пространстве

1. Центральная симметрия (симметрия относительно точки):

2. Осевая симметрия

(симметрия относительно прямой):

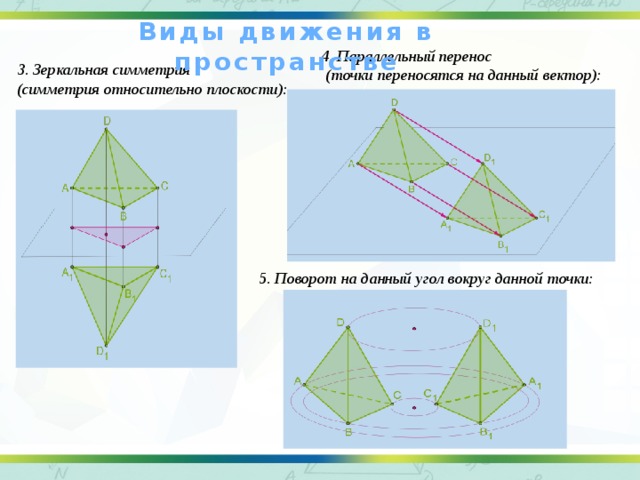
Виды движения в пространстве

4. Параллельный перенос

(точки переносятся на данный вектор):

3. Зеркальная симметрия

(симметрия относительно плоскости):

5. Поворот на данный угол вокруг данной точки:

“ Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”

Герман Вейль

• Симметрия – свойство формы или расположения фигур. Происходит от греческого «Symmetria» - соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра.

Симметрию можно обнаружить

почти везде, если знать, как ее искать.

Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии.

Творчество людей во всех своих проявлениях тяготеет к симметрии.

Центральная симметрия

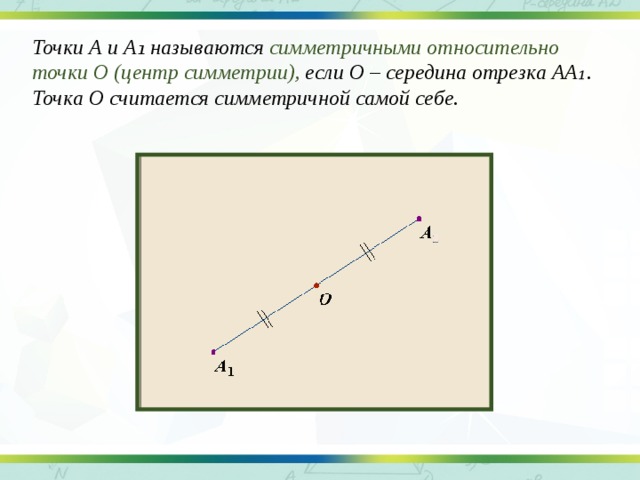
Точки А и А ₁ называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА₁.

Точка О считается симметричной самой себе.

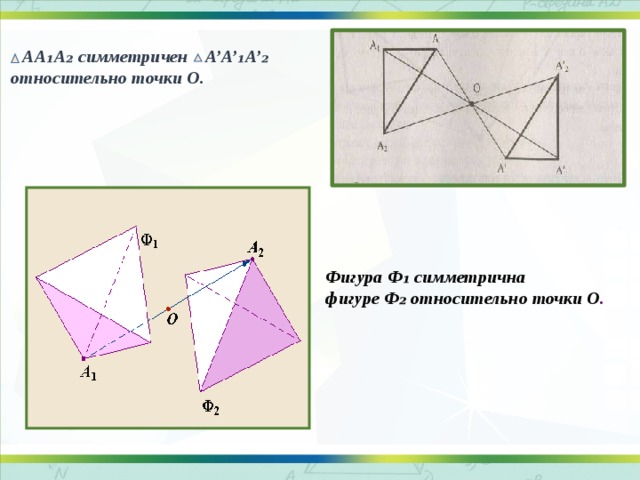
АА₁А₂ симметричен А’А’₁А’₂

относительно точки О.

Фигура Ф₁ симметрична

фигуре Ф₂ относительно точки О .

Фигура называется симметричной относительно точки О если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

Точка О называется центром симметрии фигуры.

Говорят также, что фигура обладает центральной симметрией.

Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.

Центром симметрии окружности является центр окружности , а центром симметрии параллелограмма точка пересечения его диагоналей.

Осевая

симметрия

Z

M(x; y; z)

M ₁ (x ₁ ;y ₁ ;z ₁ )

О

y

Х

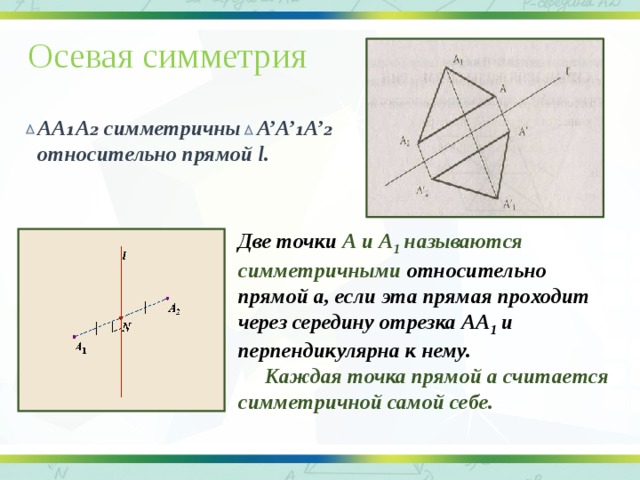
Осевая симметрия

АА₁А₂ симметричны А’А’₁А’₂

относительно прямой l.

Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему.

Каждая точка прямой а считается симметричной самой себе. 

Равнобедренный

(но не равносторонний) треугольник имеет также одну ось симметрии , а равносторонний треугольник - три основные симметрии.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.

Прямая а называется осью симметрии фигуры.

Говорят также, что фигура обладает осевой симметрией.

У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла.

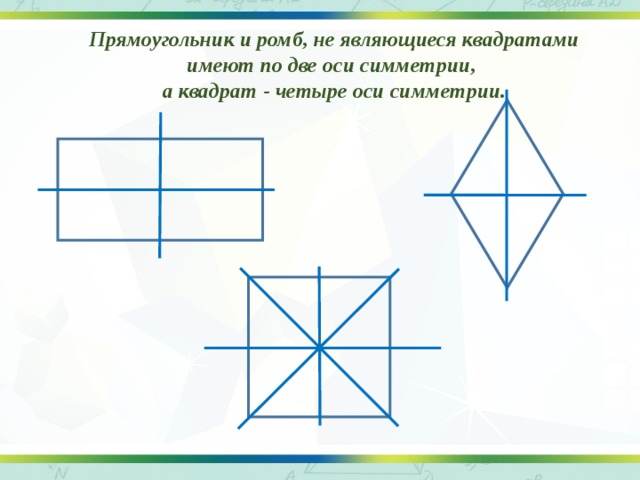
Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии,

а квадрат - четыре оси симметрии.

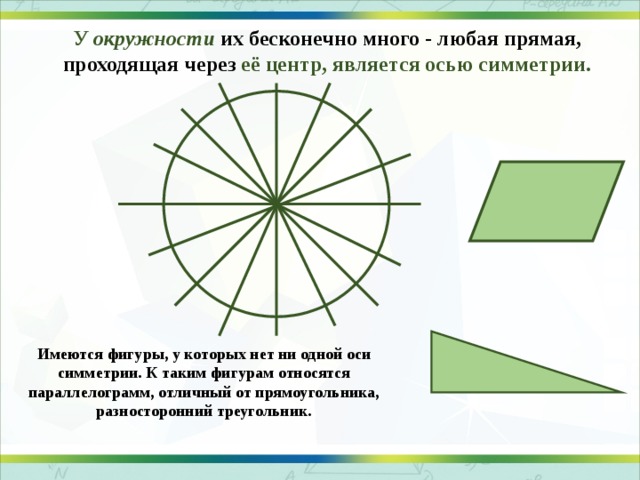
У окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

Зеркальная симметрия

Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости α точку М₁.

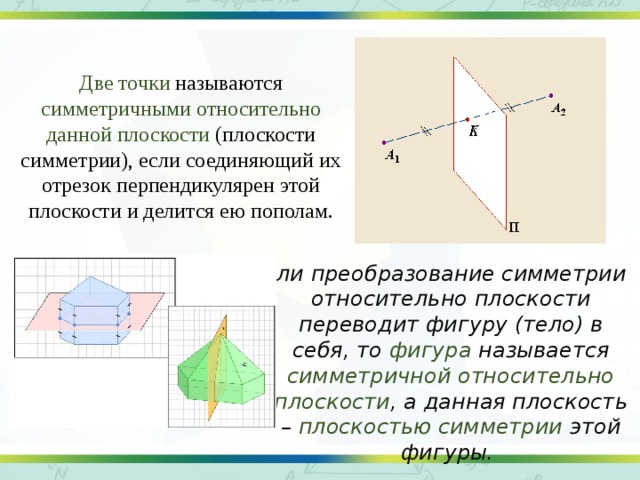
Две точки называются симметричными относительно данной плоскости (плоскости симметрии), если соединяющий их отрезок перпендикулярен этой плоскости и делится ею пополам.

Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости , а данная плоскость – плоскостью симметрии этой фигуры.

Спасибо за внимание!

Список используемой литературы и сайтов

Используемы сайты

http://video.yandex.ru/#search ...

http://video.yandex.ru/users ...

http://video.yandex.ru/users/alex ....

http://www.google.ru/imghp?hl

Литература

Геометрия. 10-11 классы: учеб. для общеобразоват. Г36 учереждений: базовый и профил. уровни/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.].- 20-е изд.- М.: Просвещение, 2011.-255 с.: ил.- (МГУ- школе).- ISBN 978-09-024966-9