Презентация к уроку геометрии в 8 классе на тему "Теорема Пифагора"

Теорема Пифагора

Урок геометрии в 8 классе

Товмурзаев В.М.

1.Найдите площадь квадрата со стороной

3 см; 1,2 мм; 5\7 м; см; а см .

2 . Найдите площадь прямоугольного

треугольника с катетами 3 см и 4 см;

2 ,2 м и 5 см; а см и в см.

3. Чему равна площадь домика?

S

= 5 см 2 ; S

= 20 см 2 .

M

Докажите,что:

F

B

4 .

C

DFCN - квадрат

D

N

K

A

«Геометрия обладает двумя великими сокровищами.Первое – это теорема Пифагора…»

О Пифагоре сохранились десятки легенд и мифов, с его именем связано многое в математике, и в первую очередь, конечно, теорема носящая его имя, которая занимает важнейшее место в школьном курсе геометрии.

Знаменитый древнегреческий философ и математик Пифагор Самосский родился на острове Самос, далеко от Греции в 580

году до н. э. По античным свидетельствам он был красив и обладал незаурядными способностями. Совсем юношей он покинул родину, прошел по дорогам Египта и 12 лет жил в Вавилоне. После возвращения домой Пифагор переселился в Италию, затем в Сицилию.

580-500 г. до н. э.

Здесь в Кретоне, рождается школа Пифагора. В пифагорейской школе занимались изучением чисел и их свойств,

много внимания уделяли музыке, живописи, физическому развитию, здоровью. Пифагор и его ученики были трудолюбивы и аскетичны.

Теорема Пифагора

В прямоугольном треугольнике

квадрат гипотенузы равен

сумме квадратов катетов .

a

b

b

а 2 +в 2 =с 2

c

a

c

Доказательство:

=( а+в) 2

=c 2 +4 · 1/2ab

S

S

c

a

c

(а+в) 2 =с 2 +4 · 1 / 2ав

b

а 2 +2ав+в 2 =с 2 +2ав

b

a

а 2 +в 2 =с 2

Смотри!

a

b

a

b

b

b

b

a

a

a

a

b

b

a

b

a

Среди пифагорейцев был распространён способ доказательства теоремы “без слов”. Слушателям представляли чертёж , на котором изображены два равных квадрата со стороной a+b, после чего писали одно слово “Смотри”.

К теореме Пифагора его ученики составляли стишки, вроде:

«Пифагоровы штаны

во все стороны равны»,

А также рисовали такие карикатуры:

Шарж из учебника XVI века.

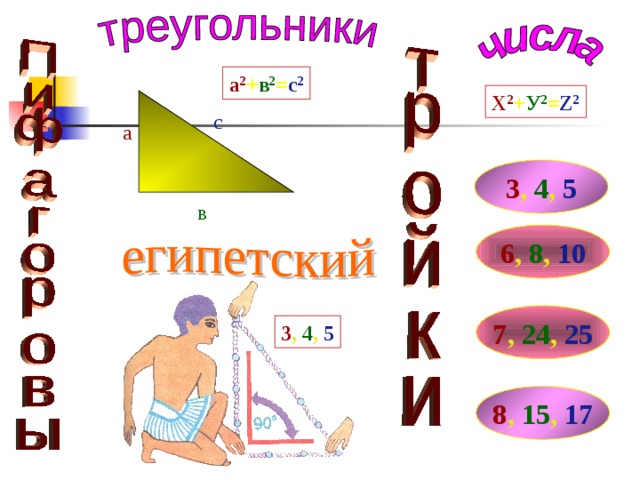
а 2 + в 2 = с 2

Х 2 + У 2 = Z 2

с

а

3 , 4 , 5

в

6 , 8 , 10

7 , 24 , 25

3 , 4 , 5

8 , 15 , 17

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса».

Заполните таблицу:

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем

а

в

6

с

8

1

1

12

12

15

13

Катеты в квадрат возводим,

Сумму степеней находим-

И таким простым путём

К результату мы придём