Презентация к уроку "Логические выражения и логические операции"

Логические выражения и логические операции.

Тема 2.

Логические выражения

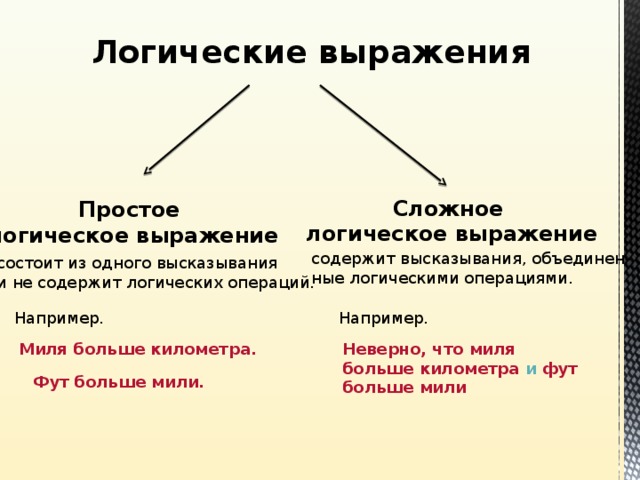
Сложное

логическое выражение

Простое

логическое выражение

содержит высказывания, объединен-

ные логическими операциями.

состоит из одного высказывания

и не содержит логических операций.

Например.

Например.

Неверно, что миля больше километра и фут больше мили

Миля больше километра.

Фут больше мили.

Логические операции

НЕ , ‾, ˥, not

Логическое отрицание (инверсия).

И , ˄ , and, &, *

Логическое умножение, (конъюнкция).

ИЛИ, ˅ , or, +

Логическое сложение (дизъюнкция).

ЕСЛИ ТО, влечет, →, if then

Логическое следование, (импликация).

~, тогда и только тогда, когда

Эквивалентность, равнозначность.

ИСТИНА – 1

ЛОЖЬ - 0

Логическое отрицание (инверсия)

Результат отрицания истинен, когда исходное высказывание ложно, и наоборот.

НЕ , ‾, ˥, not

Пример : Даны высказвания

А – «Число 10 – четное» = ИСТИНА

В – «Число 15 – отрицательное» = ЛОЖЬ

С – «Луна – спутник Земли» = ИСТИНА

– «Число 10 – нечетное» = ЛОЖЬ

– «Число 15 - положительно» = ИСТИНА

– «Луна – не спутник Земли» = ЛОЖЬ

Таблица истинности

логического отрицания

A

A

0

0

F=

1

1

1

1

0

0

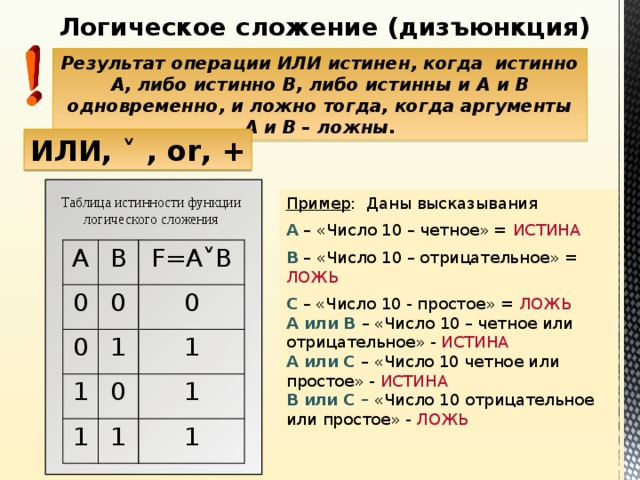
Логическое сложение (дизъюнкция)

Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинны и А и В одновременно, и ложно тогда, когда аргументы А и В – ложны.

ИЛИ, ˅ , or, +

Таблица истинности функции логического сложения

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 - простое» = ЛОЖЬ А или В – «Число 10 – четное или отрицательное» - ИСТИНА А или С – «Число 10 четное или простое» - ИСТИНА В или С – «Число 10 отрицательное или простое» - ЛОЖЬ

A

0

B

0

F=A ˅ B

0

0

1

1

1

1

0

1

1

1

Логическое умножение (конъюнкция)

Результат операции И истинен, тогда и только тогда, когда истинно одновременно высказывания А и В, и ложен во всех остальных случаях.

И , ˄ , and, &, *

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 кратно 2» = ИСТИНА А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА

Таблица истинности функции логического умножения

A

0

B

F=A ˄ B

0

0

1

0

1

1

0

0

0

1

1

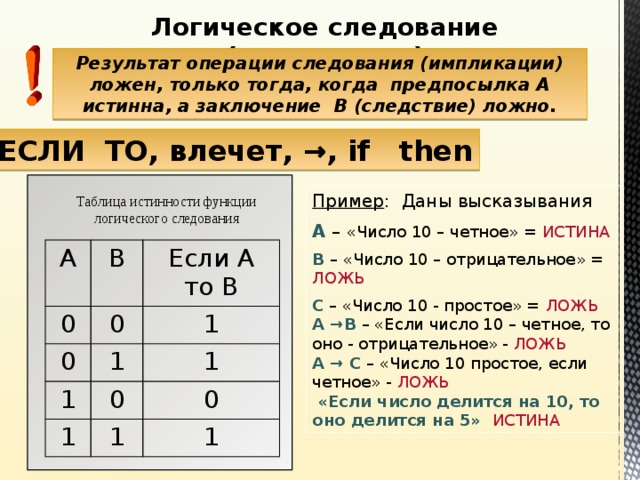
Логическое следование (импликация)

Результат операции следования (импликации) ложен, только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.

ЕСЛИ ТО, влечет, →, if then

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 - простое» = ЛОЖЬ А →В – «Если число 10 – четное, то оно - отрицательное» - ЛОЖЬ А → С – «Число 10 простое, если четное» - ЛОЖЬ «Если число делится на 10, то оно делится на 5» ИСТИНА

Таблица истинности функции логического следования

A

0

B

0

Если A то B

0

1

1

1

1

1

0

0

1

1

Эквивалентность

Результат операции эквивалентность истинен, только тогда, когда А и В одновременно истинны или одновременно ложны.

~, тогда и только тогда, когда

Таблица истинности функции эквивалентность

Пример : Даны высказывания

А – «Число 10 – четное» = ИСТИНА

В – «Число 10 – отрицательное» = ЛОЖЬ

С – «Число 10 - простое» = ЛОЖЬ А~ В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ В~С – «Число 10 такое же простое, как и отрицательное» ИСТИНА

A

0

B

0

F=A~B

0

1

1

1

1

0

0

0

1

1