© 2017, Конаков Сергей Никандрович 6410 708
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 01.06.2025 20:41
Конаков Сергей Никандрович
учитель
63 года
1 832
33 456 
Специализация
Презентация к уроку по геометрии в 8 классе "Средняя линия треугольника"
Категория:
Математика
30.09.2017 22:49
Просмотр содержимого документа
«Презентация к уроку по геометрии в 8 классе "Средняя линия треугольника"»
Применение подобия
СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
к доказательству теорем
8 класс
Л.С. Атанасян геометрия 7-9
Учиться можно только
весело…
Чтобы переваривать
знания, надо поглощать
их с аппетитом.
Анатоль Франс
1844 - 1924
Средняя линия
треугольника
Тема:
Дать определение средней линии треугольника.
Доказать теорему о средней линии треугольника.
Доказать теорему о пересечении медиан треугольника.
Цель урока
Первый признак подобия треугольников
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Второй признак подобия треугольников
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
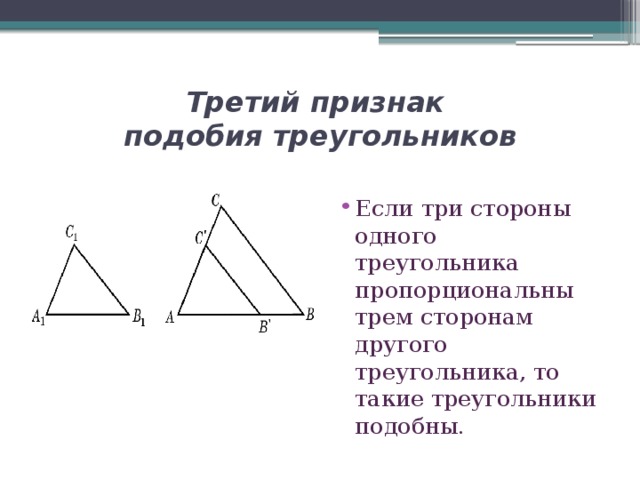
Третий признак подобия треугольников
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Основное понятие урока
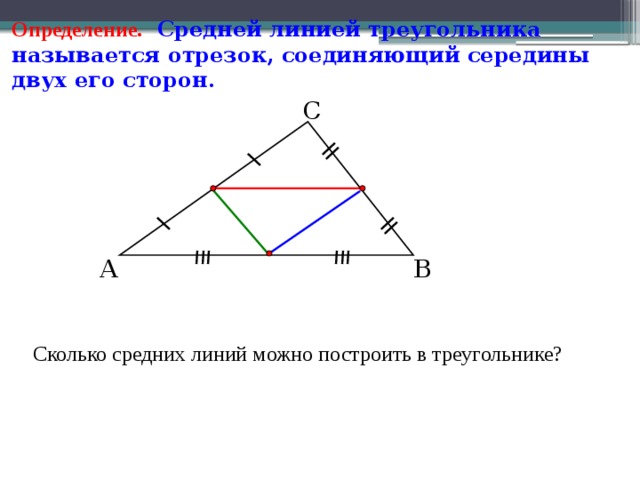
Определение. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
С
В
А
Сколько средних линий можно построить в треугольнике?
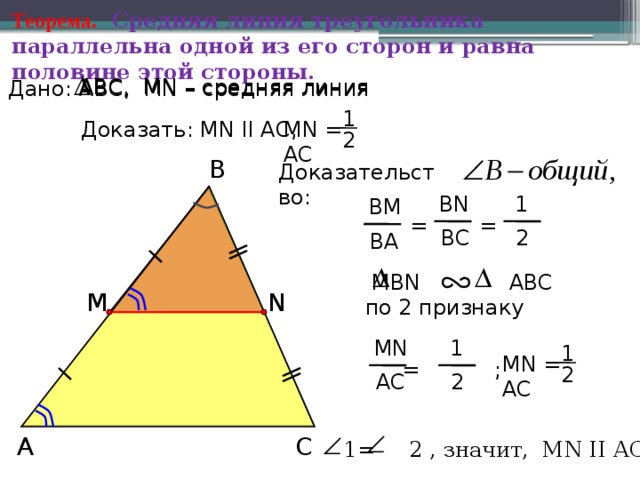
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
ABC, МN – средняя линия
Дано:
ABC, МN – средняя линия
1
Доказать: МN II АС,
MN = АС
2
B
Доказательство:
1
BN
BM
=
=
2
BC
BA
MBN ABC
по 2 признаку
N
М
MN
1
1
MN = АС
= ;
2
AC
2
C
А
1= 2 , значит, МN II АС.
9
Диктант. Задание №1
- Вариант 1
- Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Является ли этот отрезок средней линией данного треугольника?
- Вариант 2
- Точки А и В являются серединами двух сторон треугольника. Как называется отрезок АВ?
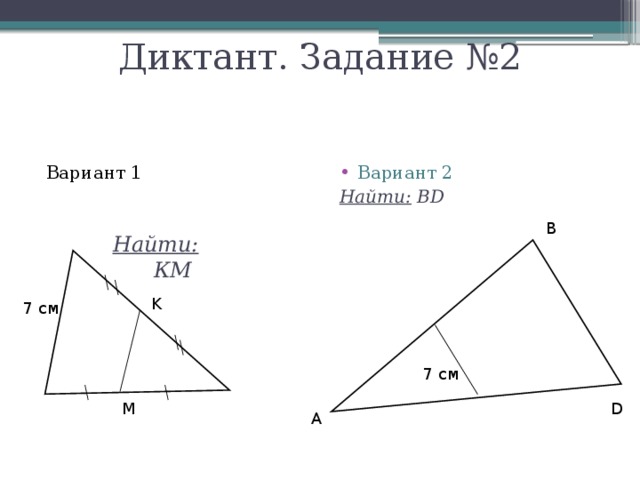
Диктант. Задание №2
Вариант 1
- Вариант 2
Найти: BD
В
Найти: КМ
K
7 см
7 см
M
D
A
Диктант. Задание №3
B
- Вариант 2
- Вариант 1
- МК=3, KN=4, MN=5
- Найти периметр треугольника АВС.
- АВ=3м, ВС=5м, АС=4м.
- Найти периметр треугольника MNK.
M
N
A
K
C
Диктант. Задание №4
- Вариант 1
- Концы отрезка АВ лежат на сторонах треугольника, а его длина равна половине третьей стороны.
- Обязательно ли: АВ – средняя линия этого треугольника?
- Вариант 2
- Концы отрезка MN лежат на сторонах треугольника. Отрезок MN параллелен третьей стороне и равен его четверти.
- Обязательно ли: MN – средняя линия этого треугольника?
Диктант. Задание №5
- Вариант 1
- Периметр треугольника равен 5,9 см. Найти периметр треугольника, отсекаемого одной из его средних линий.
- Вариант 2
- Периметр треугольника равен 7,3 см. Найти периметр треугольника, отсекаемого одной из его средних линий.
Элементы треугольника
Медиана треугольника –
отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис. 1).
Биссектриса треугольника –
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной стороны (рис. 2).
В режиме слайдов ответы появляются после кликанья мышкой
Высота треугольника –
отрезок, соединяющий вершину треугольника с точкой противоположной стороны или ее продолжения и перпендикулярный этой стороне (рис. 3).
12
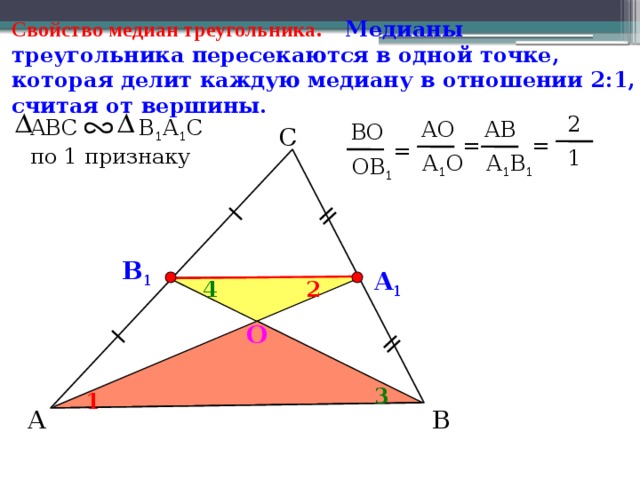
Свойство медиан треугольника . Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
2
AВС В 1 А 1 С
по 1 признаку
АВ
АО
ВО
С
=
=
=
1
А 1 В 1
А 1 О
ОВ 1
В 1
А 1
2
4
О
3
1
В
А
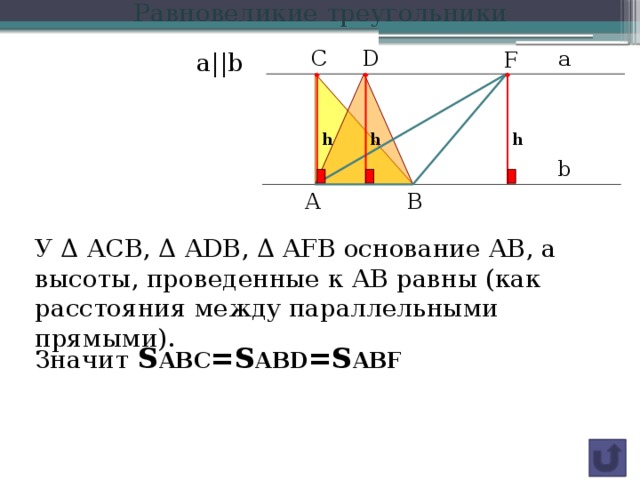
Равновеликие треугольники
D
C
а
F
а||b
h
h
h
b
B
A
У Δ АСВ, Δ АDB, Δ AFB основание АВ, а высоты, проведенные к АВ равны (как расстояния между параллельными прямыми).
Значит S ABC =S ABD =S ABF
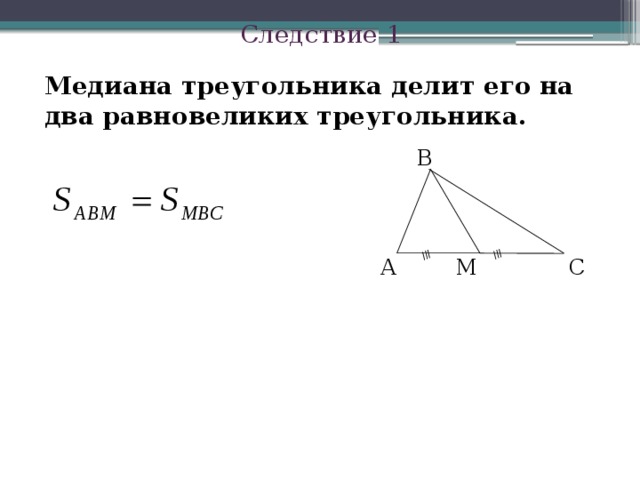
Следствие 1
Медиана треугольника делит его на два равновеликих треугольника.
В
А
С
М
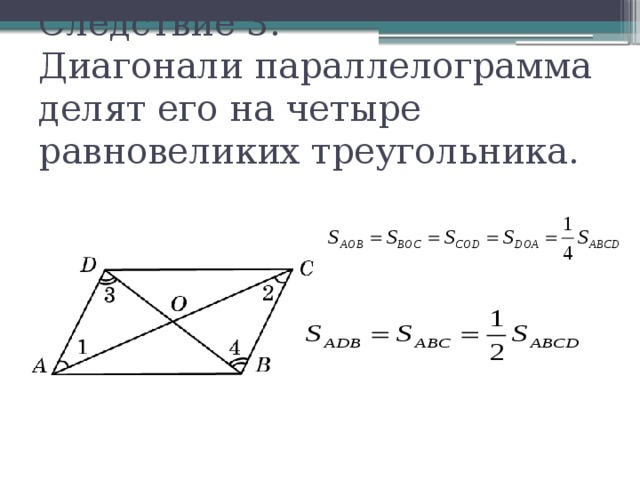
Следствие 3. Диагонали параллелограмма делят его на четыре равновеликих треугольника.
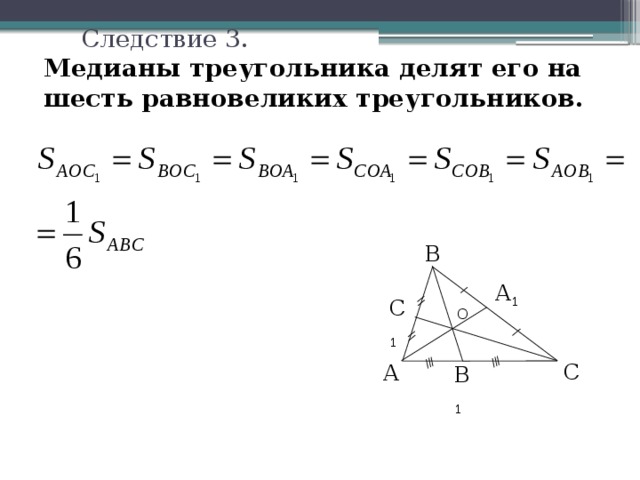
Следствие 3.
Медианы треугольника делят его на шесть равновеликих треугольников.
В
А 1
С 1
О
С
А
В 1
Доказать на уроке
Следствие 3.
Средняя линия треугольника отсекает от данного треугольник, площадь которого равна площади исходного треугольника.
B
M
N
A
K
C
S СМК = S МКЕ = ½ S МЕС = ¼ . В треугольнике МКЕ (по свойству точки пересечения медиан) ЕО:ОМ = 2:1 =S ЕКО : S МОК = 2:1, т.е. S МОК = ⅓ S МКЕ = ⅓ ·¼ = 1/12. S MOK :S CMK = (1/12) : (1/4) = 1:3. К О В С М " width="640"
Задача
Медианы ВК и ЕМ треугольника ВСЕ пересекаются в точке О. Найти S MOK :S CMK .
Е
Решение. Обозначим S АВС = 1. S МЕС = ½ . В треугольнике СМЕ МК – медиана = S СМК = S МКЕ =
½ S МЕС = ¼ .
В треугольнике МКЕ (по свойству точки пересечения медиан) ЕО:ОМ = 2:1 =S ЕКО : S МОК = 2:1, т.е. S МОК = ⅓ S МКЕ = ⅓ ·¼ = 1/12.
S MOK :S CMK = (1/12) : (1/4) = 1:3.
К
О
В
С
М
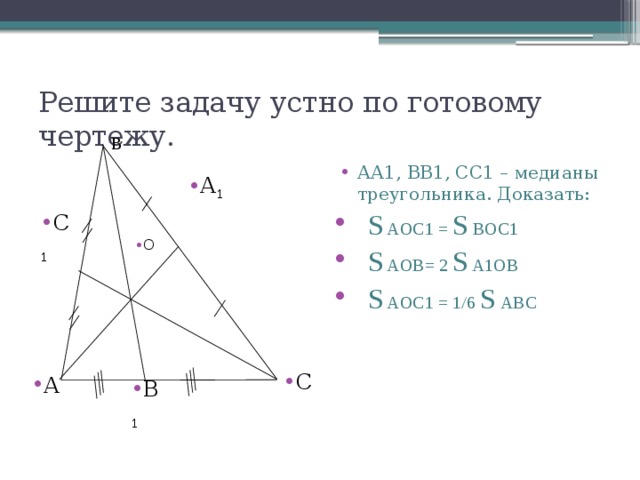
Решите задачу устно по готовому чертежу.
В
- АА1, ВВ1, СС1 – медианы треугольника. Доказать:
- S AOC1 = S BOC1
- S AOB= 2 S A1OB
- S AOC1 = 1/6 S АВС
- А 1
- С 1
- О
- С
- А
- В 1
Итог урока
- Отрезок , соединяющий середины двух сторон треугольника, называется средней линией треугольника .
- Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
- Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
- Средняя линия треугольника отсекает от данного треугольник, площадь которого равна ¼ площади исходного.
- Три средние линии треугольника разбивают его на 4 равоновеликих треугольника, площадь каждого из них равна ¼ площади исходного.
23
П. 62, вопросы 8, 9 (стр. 160)
Задачи № 616, 571.
Домашнее задание
Спасибо за урок!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
