Презентация к уроку по теме: "Свойства функции"

Свойства функции

«Производная. Точки экстремума и перегиба.

Возрастание и выпуклость функции»

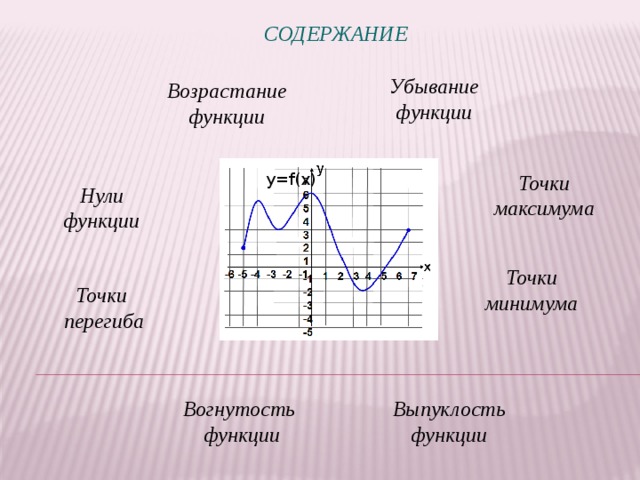
СОДЕРЖАНИЕ

Убывание

функции

Возрастание

функции

y=f(x)

Точки

максимума

Нули

функции

Точки

минимума

Точки

перегиба

Вогнутость

Выпуклость

функции

функции

0 у0 y=f(x) у0 Теорема: Если производная на промежутке положительная, то функция y=f(x) на данном промежутке возрастает. " width="640"

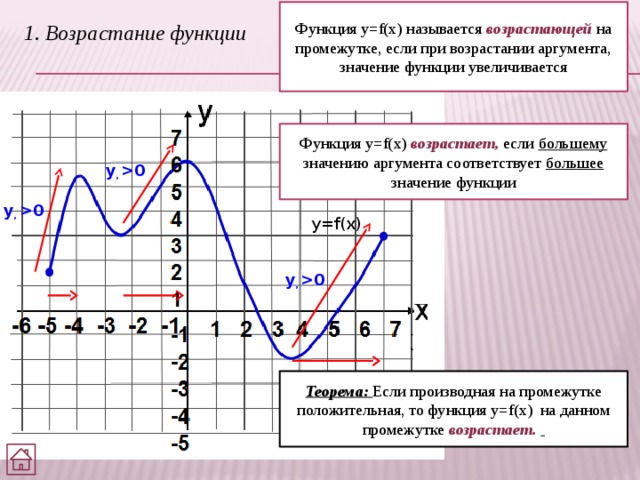
Функция y=f(x) называется возрастающей на промежутке, если при возрастании аргумента, значение функции увеличивается

1. Возрастание функции

Функция y=f(x) возрастает, если большему значению аргумента соответствует большее значение функции

у0

у0

y=f(x)

у0

Теорема: Если производная на промежутке положительная, то функция y=f(x) на данном промежутке возрастает.

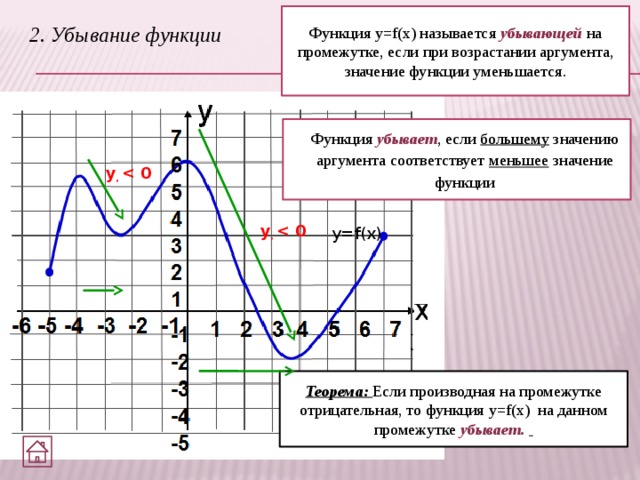
Функция y=f(x) называется убывающей на промежутке, если при возрастании аргумента, значение функции уменьшается.

2. Убывание функции

Функция убывает , если большему значению аргумента соответствует меньшее значение функции

у

у

y=f(x)

Теорема: Если производная на промежутке отрицательная, то функция y=f(x) на данном промежутке убывает.

0 x 0 у у0 y=f(x) Распознать точку максимума по графику функции очень просто. График функции в окрестности точки максимума выглядят как гладкий “холм” у у0 x x max " width="640"

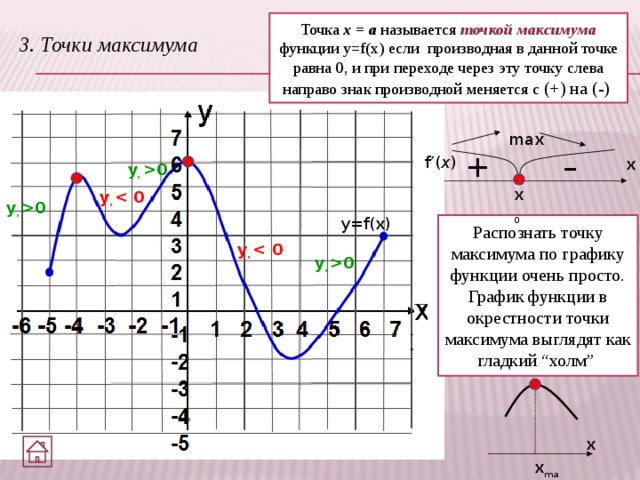
Точка х = а называется точкой максимума функции y=f(x) если производная в данной точке равна 0, и при переходе через эту точку слева направо знак производной меняется с (+) на (-)

3. Точки максимума

max

–

+

f  ( x )

x

у0

x 0

у

у0

y=f(x)

Распознать точку максимума по графику функции очень просто. График функции в окрестности точки максимума выглядят как гладкий “холм”

у

у0

x

x max

0 x 0 у у0 y=f(x) Распознать точку минимума по графику функции очень просто. График функции в окрестности точки минимума выглядят как гладкая “впадина” у у0 Точки минимума и точки максимума называются точками экстремума. x x min " width="640"

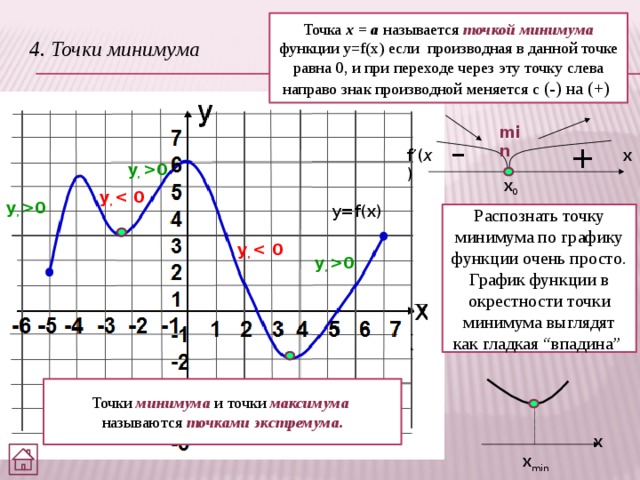
Точка х = а называется точкой минимума функции y=f(x) если производная в данной точке равна 0, и при переходе через эту точку слева направо знак производной меняется с (-) на (+)

4. Точки минимума

min

–

+

x

f  ( x )

у0

x 0

у

у0

y=f(x)

Распознать точку минимума по графику функции очень просто. График функции в окрестности точки минимума выглядят как гладкая “впадина”

у

у0

Точки минимума и точки максимума называются точками экстремума.

x

x min

касательная

касательная

касательная

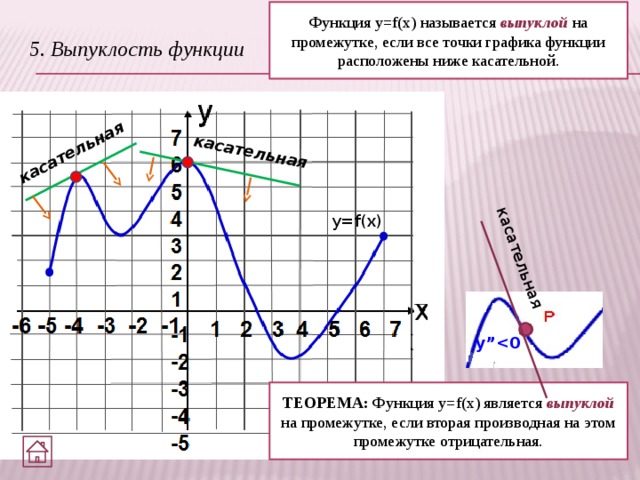
Функция y=f(x) называется выпуклой на промежутке, если все точки графика функции расположены ниже касательной.

5. Выпуклость функции

y=f(x)

у”

ТЕОРЕМА: Функция y=f(x) является выпуклой на промежутке, если вторая производная на этом промежутке отрицательная.

0 y=f(x) у”0 у”0 ТЕОРЕМА: Функция y=f(x) является вогнутой на промежутке, если вторая производная на этом промежутке положительная. " width="640"

касательная

касательная

касательная

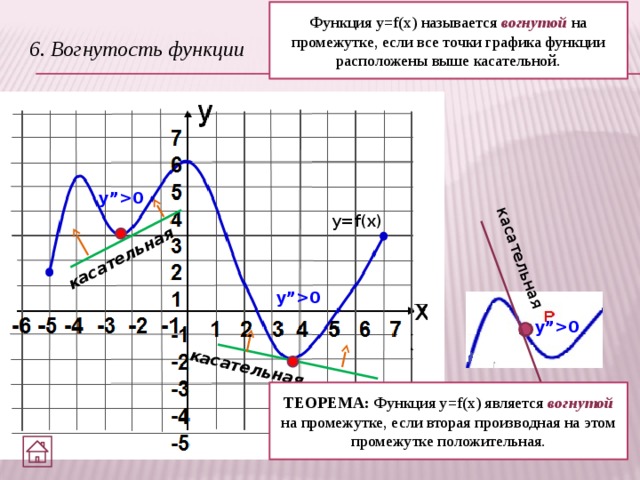
Функция y=f(x) называется вогнутой на промежутке, если все точки графика функции расположены выше касательной.

6. Вогнутость функции

у”0

y=f(x)

у”0

у”0

ТЕОРЕМА: Функция y=f(x) является вогнутой на промежутке, если вторая производная на этом промежутке положительная.

0 y=f(x) P 1 у” P 3 у”0 Р " width="640"

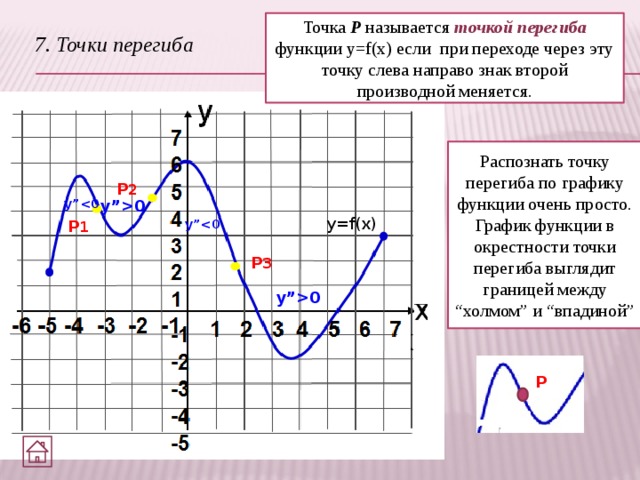
Точка Р называется точкой перегиба функции y=f(x) если при переходе через эту точку слева направо знак второй производной меняется.

7. Точки перегиба

• P 1

Распознать точку перегиба по графику функции очень просто. График функции в окрестности точки перегиба выглядит границей между “холмом” и “впадиной”

P 2

у”

у”0

y=f(x)

P 1

у”

P 3

у”0

Р

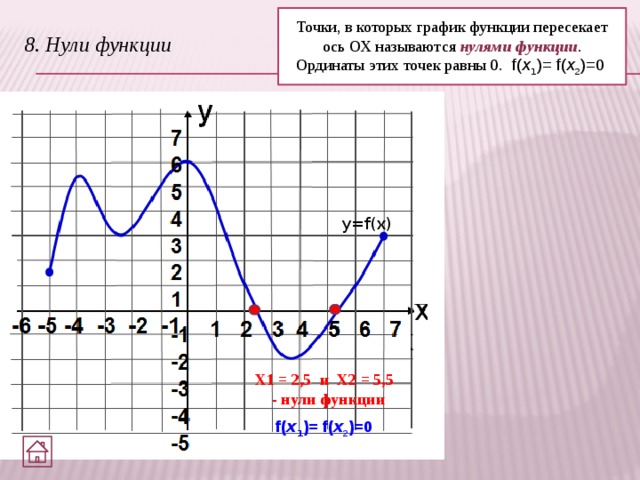
Точки, в которых график функции пересекает ось ОХ называются нулями функции .

Ординаты этих точек равны 0. f( x 1 )= f( x 2 )=0

8. Нули функции

y=f(x)

X1 = 2,5 и X2 = 5,5

- нули функции

f( x 1 )= f( x 2 )=0

Список литературы:

Учебник : Богомолов, Н. В. Практические занятия по математике: учеб. пособие для студентов сред. проф. учеб. заведений

Презентация может быть использована на уроках математики для формирования умения формулировать свойства графиков функций, с применением производной по теме «Производная. Точки экстремума и перегиба. Возрастание и выпуклость функции».

Петрозаводск 2013г