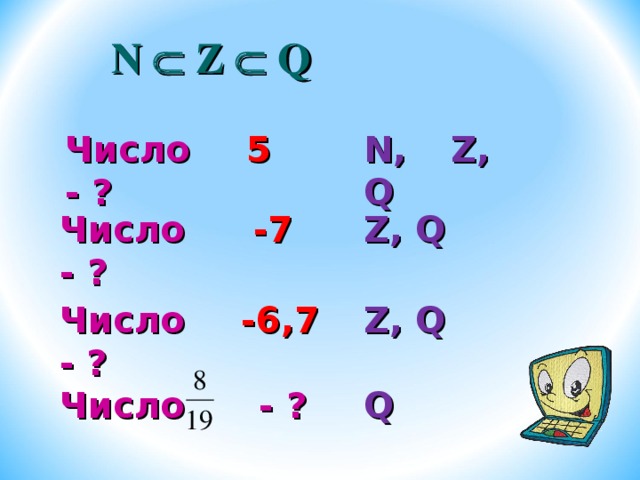Презентация по алгебре по теме "Рациональные числа" (8 класс)

Обухова Наталия Семеновна, МОУ СОШ №17 г.Заволжья Нижегородской области

Для счета предметов используются числа, которые называются натуральными . Для обозначения множества натуральных чисел употребляется буква N - первая буква латинского слова Naturalis - «естественный», «натуральный»

N - натуральные

1 , 2, 3, 4, 5, …

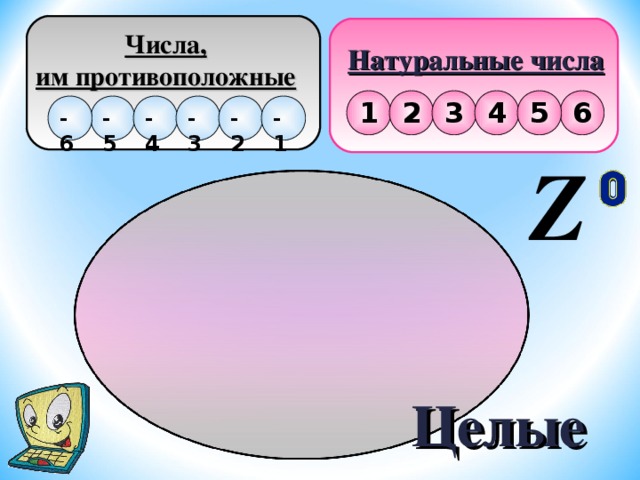
Числа,

им противоположные

Натуральные числа

5

3

6

4

2

1

-5

-4

-3

-2

-6

-1

Целые

Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z - первой буквой немецкого слова Zahl - «число».

Z - целые

… , -3, -2, - 1 , 0,

1 , 2, 3, …

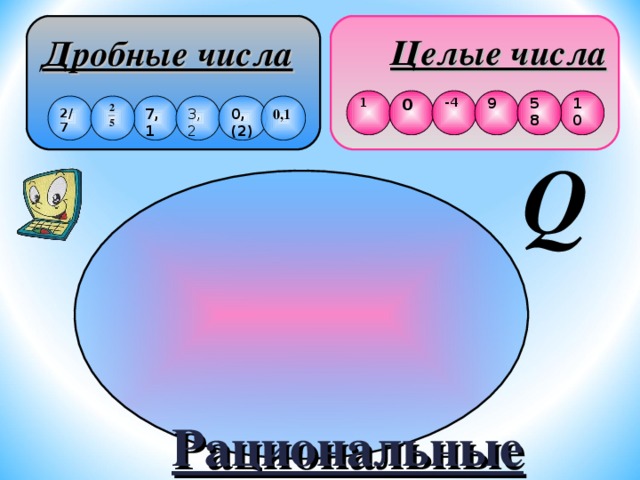
Целые числа

Дробные числа

58

10

9

-4

0

1

7,1

0,1

2/7

3,2

0,(2)

Рациональные

Множество чисел, которое можно представить в виде , называется множеством рациональных чисел и обозначается буквой Q - первой буквой французского слова Quotient - «отношение». Есть также версия, что название рациональных чисел связано с латинским словом ratio – разум.

Q - рациональные

… , -3, -2, - 1 , 0, 1, 2, 3, …

+ дроби

Отношения между множествами натуральных,

целых и рациональных чисел наглядно демонстрирует

геометрическая иллюстрация – круги Эйлера .

N  Z  Q

Математический символ   ∈   называют знаком принадлежности ( элемент принадлежит множеству ) .

«n - натуральное число»

можно писать n ∈ N  

«m - целое число»

можно писать m ∈ Z

«r - рациональное число»

можно писать r ∈ Q  

Математический символ ⊂  называют знаком включения ( одно множество содержится в другом ).

«N - часть множества Z»

можно писать N ⊂ Z ,

«Z - часть множества Q»

можно писать Z ⊂ Q  

Множества обозначают большими буквами,

элементы множества - маленькими буквами.

«x  не принадлежит множеству X» 

можно писать x ∉ X

«A  не является частью (подмножеством) B»

можно писать A  B .

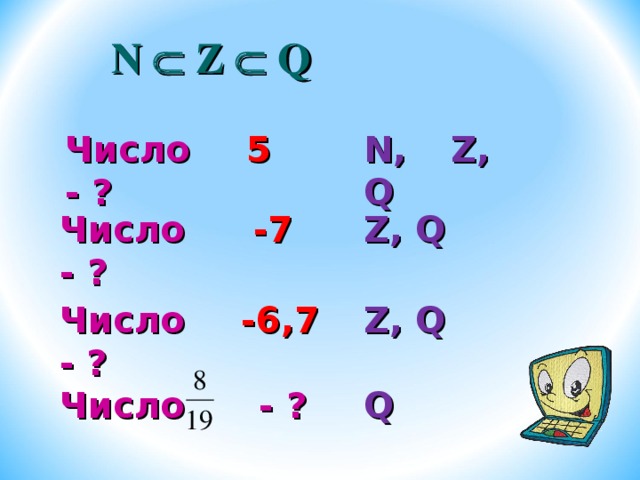
N  Z  Q

Число 5 - ?

N, Z, Q

Число -7 - ?

Z, Q

Z, Q

Число -6,7 - ?

Число - ?

Q

Переведите обыкновенные дроби в десятичные:

= 0,375 – конечная десятичная дробь

Если в знаменателе стоят 2, 5, их произведение или произведение комбинацийэтих чисел – всегда КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ!

Переведите обыкновенные дроби в десятичные:

= 0,272727272727272727… - бесконечная периодическая десятичная дробь

Для краткости написания – ПЕРИОД (круглые скобки)

0,272727272727272727…= 0,(27)

Прочитайте дроби:

• 0,(2) 2) 2,(21) 3) 1,(1)

• 0,(2) 2) 2,(21) 3) 1,(1)

4) -3,0(3) 5) -0,1(6) 6) 12,45(7)

4) -3,0(3) 5) -0,1(6) 6) 12,45(7)

чисто периодические

смешанные периодические

Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?

N  Z  Q

5 = 5,000… = 5,(0)

-8,37 = -8,37000… = -8,37(0)

Дроби - ?

Алгоритмы перевода рациональных чисел

в бесконечную десятичную периодическую дробь

= 0,375 = 0,375(0)

= 0,272727… = 0,(27)

Делим числитель

на знаменатель

Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?

Переведем б.п.д. дробь 0,(2)

в обыкновенную

Пусть х = 0,(2)

Это для

чисто периодической !!!

10х = 2,(2)

10х = 2,(2)

 10 ( число цифр в периоде )

х = 0,(2)

10х – х = 2,(2) - 0,(2)

9х = 2

0,(2)

Переведем б.п.д. дробь 0,4(6)

в обыкновенную

Это для

смешанной периодической !!!

Пусть х = 0,4(6)

10х = 4,(6)

100х = 46,(6)

 10 ( число цифр в периоде )

10х = 4,(6)

100х – 10х = 46,(6) - 4,(6)

90х = 42

0,4(6)

21