Презентация по теме: "Цилиндр"

,,,,,

,,

,,

,,,

Знаете ли Вы…

Слово «цилиндр» произошло от греческого слова «кюлиндрос», означающего «валик», «каток».

На рубеже 18-19 веков были модны шляпы с небольшими полями, которые назывались цилиндрами .

Что объединяет эти предметы?

форма

образующая

II

Рассмотрим

Множество отрезков образующих определяют цилиндрическую поверхность. Сами отрезки называются образующими цилиндрической поверхности .

А 1

А

5

образующая

Тело ограниченное цилиндрической поверхностью и двумя кругами, называется цилиндром.

O 1

А 1

O

А

6

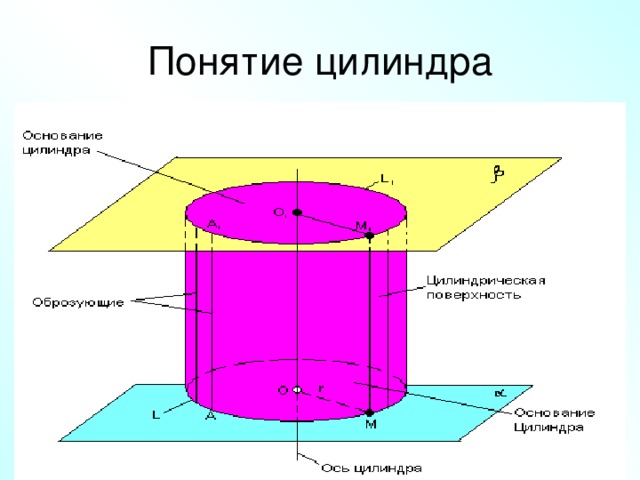
Понятие цилиндра

Длина образующей называется высотой цилиндра,

а радиус основания – радиусом цилиндра.

AA 1 II BB 1

AA 1 = BB 1

O 1

r

А 1

B 1

h

O

А

B

9

Цилиндр может быть получен путем вращения прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника АВСD вокруг стороны АВ. Боковая поверхность образуется вращением стороны СD, а основания – вращением сторон ВС и АD.

А

D

В

С

9

Виды цилиндров

Прямой круговой цилиндр .

Наклонный цилиндр

Получен вращением прямоугольника ABCD вокруг АВ.

Образующие цилиндра не перпендикулярны его основаниям.

Сложные цилиндры.

Основание –

часть параболы

Основание - эллипс

Виды сечений цилиндра

Сечение цилиндра плоскостью, проходящей через его ось, называется осевым сечением .

Цилиндр, осевое сечение которого – квадрат, называется

равносторонним .

Виды сечений цилиндра

Сечением цилиндра плоскостью, параллельной основанию, является круг .

Виды сечений цилиндра

Сечением цилиндра плоскостью, перпендикулярной основанию, является прямоугольник.

Развёртка цилиндра

Н

С= 2ПR

Развертка состоит из боковой поверхности (прямоугольника) и двух оснований ( кругов )







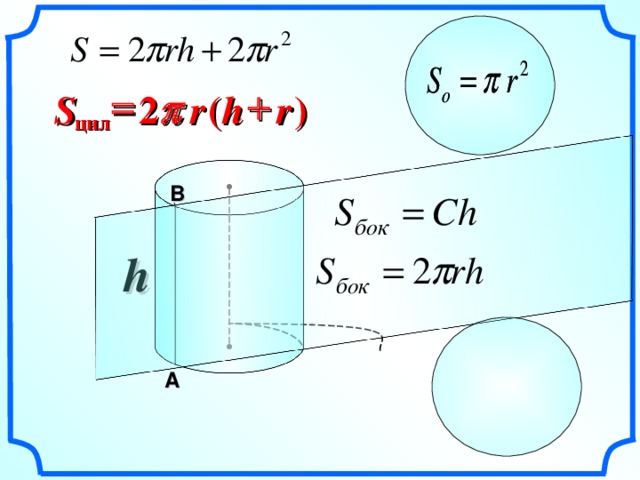
r

2

(

)

h

r

S

цил

В

h

А

16

№ 521 . Найдите диагональ осевого сечения цилиндра, если радиус основания 1,5 м, а высота – 4 м.

С

В

4

5

D

3

А

17

№ 527.

Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: 1) h, если r = 10 дм, d = 8 дм, АВ = 13 дм; 2) d, если h = 6 см, r = 5 см, АВ = 10 см.

А

Повторение

a b

O 1

К

a

Р

Опорный чертеж к задачам 527, 529, 530.

b

O

a II

В

18

Повторение

Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ.

О

65 0

65 0

В

А

19

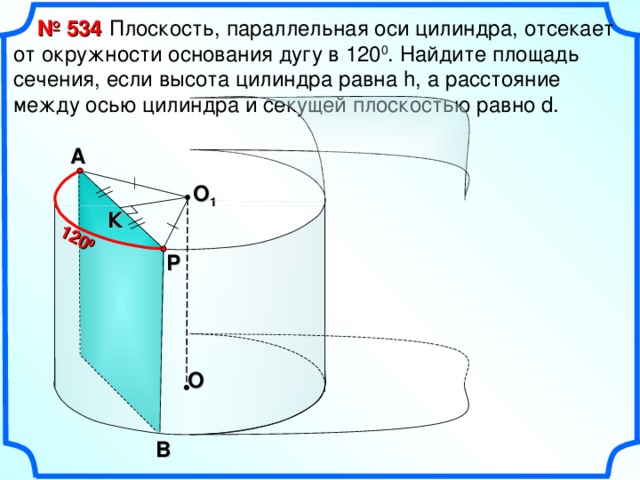
120 0

№ 534

Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120 0 . Найдите площадь сечения, если высота цилиндра равна h, а расстояние между осью цилиндра и секущей плоскостью равно d.

А

O 1

К

Р

Опорный чертеж к задачам 534, 535.

O

В

20

Осевое сечение цилиндра – квадрат, длина диагонали которого 24 см. Найдите радиус основания цилиндра и площадь боковой поверхности.

А

D

24

В

С

20