Презентация подготовка к егэ по информатике

МКОУ "Рубасская СОШ" Проект На тему: « Подготовка к ЕГЭ. Тесты по темам курса «Информатика и ИКТ»»

Юнусов У.Б.

Учитель информатики и ИКТ

МКОУ «Рубасская СОШ» Дербентского района РД

с.Рубас -2017-

Цели проекта:

• Проанализировать тесты ЕГЭ по темам курса «Информатика и ИКТ»
• Рассмотреть межпреметную связь в тестах ЕГЭ.
• Выявить достоинства и недостатки тестов ЕГЭ. (срок достижения цели 17.12.2018 г.)

Тематические блоки тестов ЕГЭ.

• Информация и ее кодирование.
• Алгоритмизация и программирование.
• Моделирование и компьютерный эксперимент.
• Основы логики.
• Технологии обработки информации.
• Телекоммуникационные технологии.
• Технология программирования.

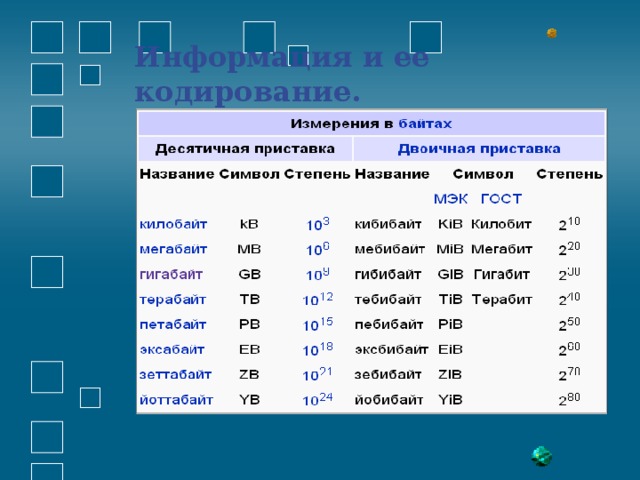
Информация и ее кодирование.

Информация и ее кодирование.

Задача 1.

• Сколько единиц в двоичной записи числа 1025?

1) 1 2) 2 3) 10 4) 11

• Решение.

1025=1024+1

1024 10 =2^10

В двоичной С.С. имеет вид: 10000000000 2

Тогда 10000000000 2 + 1 2 = 10000000001 2

Ответ: 2 единицы.

Информация и ее кодирование.

Задача 2. Сколько единиц в двоичной записи числа 1025?

1) 1 2) 2 3) 10 4) 11

• Решение.

1025=1024+1

1024 10 =2^10

В двоичной С.С. имеет вид: 10000000000 2

Тогда 10000000000 2 + 1 2 = 10000000001 2

Ответ: 2 единицы.

Информация и ее кодирование.

Задача 3. Текстовое сообщение в кодировке ASCII было переведено в кодировку Unicode. Как изменится объём этого сообщения, если оно состояло из фразы В.И. Даля:

«Язык есть вековой труд целого поколения»

• Увеличится на 41 бит 2. Уменьшится на 320 бит

• Увеличится на 40 байт 4. Уменьшится на 39 байт

Решение.

Количество символов – 40 Объём в ASCII 40 байт (1 символ 8 бит или 1 байт)

Объём в Unicode 80 байт (1 символ 16 бит или 2 байта)

Ответ: увеличится на 40 байт

Задача1. Определите значение переменной c после выполнения следующего фрагмента программы ( записанного ниже на разных языках программирования ).

a := 40;

b := 80;

b := - a - 2 * b;

if a

Ответ: 280.

Алгоритмизация и программирование.

Основы логики.

Основные логические операции:

логическое отрицание (инверсия) – « не »; ¬ ; ¯ ;

• логическое умножение (конъюнкция) – « и »; & ; ^ ; • ;
• логическое сложение (дизъюнкция) – « или »; + ;  ;
• логическое следование (импликация) –  
• логическая операция эквивалентности – ~ ;  ;  ;
• функция Вебба (отрицание дизъюнкции) – ИЛИ-НЕ ;
• функция Шеффера (отрицание конъюнкции) – И-НЕ ;
• сложение по модулю 2 (М2).

Основы логики.

Задача 1.

Укажите, какое логическое выражение равносильно выражению

A  ¬(¬B  C) 1 . ¬A  ¬B  ¬C 2. A  ¬B  ¬C

3 . A  B  ¬C 4 . A  ¬B  C

• Применим формулу де Моргана, а затем закон двойного отрицания:

A  ¬(¬B  C) =

2. Перепишем ответы в других обозначениях:

• ¬A  ¬B  ¬C = A  ¬B  ¬C = A  B  ¬C = A  ¬B  C =
• ¬A  ¬B  ¬C =
• A  ¬B  ¬C =
• A  B  ¬C =
• A  ¬B  C =

Таким образом, правильный ответ – 3 .

2)→(X 3)) ? 1) 1 2) 2 3) 3 4) 4 Решение. ) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем результаты сравнения в двух внутренних скобках: Ответ 3. " width="640"

Основы логики.

Задача 2.

Для какого из указанных значений X истинно высказывание

¬((X 2)→(X 3)) ?

1) 1 2) 2 3) 3 4) 4

Решение.

) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем результаты сравнения в двух внутренних скобках:

Ответ 3.

Основы логики.

Задача 3. Сколько различных решений имеет уравнение

• ((K  L) → (L  M  N)) = 0

где K, L, M, N – логические переменные?

В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов

Решение. Перепишем уравнение, используя более простые обозначения операций: ((K + L) → (L · M · N)) = 0.

• Из таблицы истинности операции «импликация» следует, что это равенство верно тогда и только тогда, когда одновременно K + L = 1 и L · M · N = 0.

• Из уравнения следует, что хотя бы одна из переменных, K или L равна 1 или обе вместе; поэтому рассмотрим три случая.

K = 1 и L = 0; K = 1 и L = 1; K = 0 и L = 1.

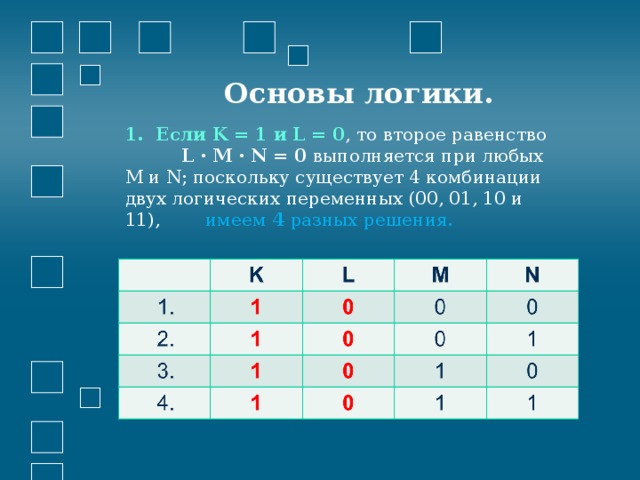
Основы логики.

1. Если K = 1 и L = 0 , то второе равенство L · M · N = 0 выполняется при любых М и N; поскольку существует 4 комбинации двух логических переменных (00, 01, 10 и 11), имеем 4 разных решения.

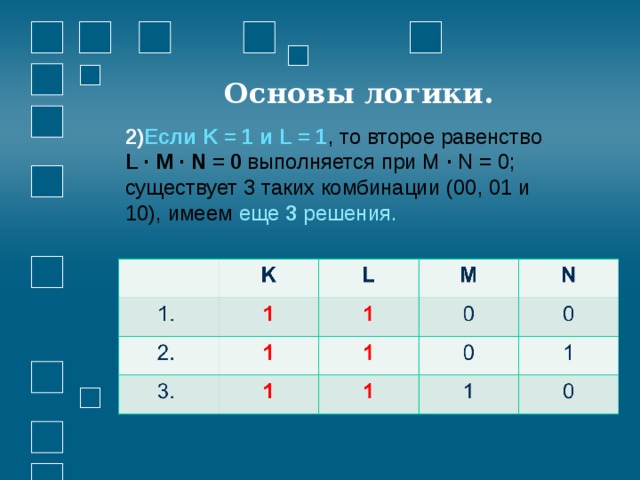
Основы логики.

• Если K = 1 и L = 1 , то второе равенство L · M · N = 0 выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения.

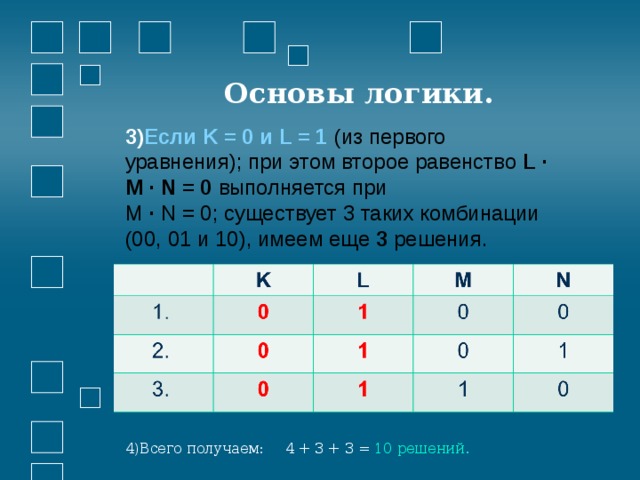
Основы логики.

• Если K = 0 и L = 1 (из первого уравнения); при этом второе равенство L · M · N = 0 выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения.

• Всего получаем: 4 + 3 + 3 = 10 решений.

Технологии обработки информации.

Задача1. Все 5-буквенные слова, составленные из букв А,О,У, записаны в алфавитном порядке.

Вот начало списка.

• ААААА 2. ААААО 3. ААААУ 4. АААОА … .

Запишите слово, которое стоит на 240-м месте от начала списка.

Решение.

Обозначим А-0, О-1, У-2 и запишем полученное:

• 00000 2. 00001 3. 00002 4. 00010

Заметим, что коды записаны в троичной системе счисления,

Тогда на 240 месте будет стоять число 239, т. к. на 1-м месте стоит число 0. Переведем число 239 в троичную с.с.

Получим: 22212 Поэтому ответом будет УУУОУ

Ответ: УУУОУ.

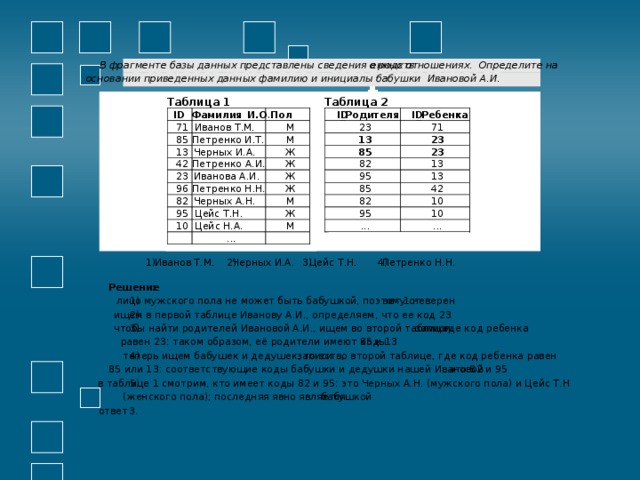
енных отношениях. Определите на

В фрагменте базы данных представлены сведения о родств

основании приведенных данных фамилию и инициалы бабушки Ивановой А.И.

Таблица 2

Таблица 1

Технологии обработки информации.

Фамилия_И.О.

Пол

_Родителя

_Ребенка

ID

ID

ID

23

М

71

Иванов Т.М.

71

М

23

85

Петренко И.Т.

13

13

23

85

Ж

Черных И.А.

82

42

Петренко А.И.

Ж

13

Ж

95

Иванова А.И.

23

13

42

Петренко Н.Н.

Ж

85

96

10

82

82

Черных А.Н.

M

Цейс Т.Н.

95

95

10

Ж

М

...

Цейс Н.А.

10

...

...

3)

4)

1)

Черных И.А.

2)

Петренко Н.Н.

Иванов Т.М.

Цейс Т.Н.

:

Решение

1)

лицо мужского пола не может быть бабушкой, поэтому от

вет 1 неверен

2)

ищем в первой таблице Иванову А.И., определяем, что ее код 23

3)

чтобы найти родителей Ивановой А.И., ищем во второй таблице

записи

, где код ребенка

85 и 13

равен 23: таком образом, её родители имеют коды

теперь ищем бабушек и дедушек, то есть,

записи во второй таблице, где код ребенка равен

4)

–

это 82 и 95

85 или 13: соответствующие коды бабушки и дедушки нашей Ивановой

в таблице 1 смотрим, кто имеет коды 82 и 95: это Черных А.Н. (мужского пола) и Цейс Т.Н

5)

(женского пола); последняя явно является

бабушкой

ответ

3.

Задача 3.

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,2 2) 2 3) 3 4) 4

Решение:

так как частота дискретизации 16 кГц, за одну секунду запоминается 16000 значений сигнала

так как глубина кодирования – 24 бита = 3 байта, для хранения 1 секунды записи требуется

16000  3 байта = 48 000 байт

(для стерео записи – в 2 раза больше)

на 1 минуту = 60 секунд записи потребуется

60  48000 байта = 2 880 000 байт,

то есть около 3 Мбайт

Таким образом, правильный ответ – 3.

• Задача 4.
• В ячейке B4 электронной таблицы записана формула = $C3*2. Какой вид приобретет формула, после того как ячейку B4 скопируют в ячейку B6? Примечание: знак $ используется для обозначения абсолютной адресации.
• 1) =$C5*4 2) =$C5*2 3) =$C3*4 4) =$C3*2
• Решение:
• ссылка $C3 – это смешанная ссылка, в которой «заблокирован» столбец C, а строка 3 – это относительный адрес;
• после того, как ячейку B4 скопировали в B6, номер строки увеличился на 2, поэтому и в ссылке $C3 номер строки (относительная часть) также увеличится на 2, ссылка превратится в $C5
• константы при копировании формул не меняются, поэтому получится =$C5*2
• таким образом, правильный ответ – 2.

Телекоммуникационные технологии.

Задача 1. Скорость передачи данных через ADSL-соединение равна 512 000 бит/c. Передача файла через это соединение заняла 1 минуту. Определить размер файла в килобайтах.

Решение:

выделим в заданных больших числах степени двойки; переведем время в секунды (чтобы «согласовать» единицы измерения), а скорость передачи – в Кбайты/с, поскольку ответ нужно получить в Кбайтах:

1 мин = 60   с = 4 · 15 с = 2 2 · 15 с

512000 бит/c = 512 · 1000 бит/с = 2 9 · 125 · 8 бит/с = 2 9 · 5 3 · 2 3 бит/с = 2 12 · 5 3 бит/с = 2 9 · 5 3 байт/с = Кбайт/с = Кбайт/с

чтобы найти время объем файла, нужно умножить время передачи на скорость передачи:

Кбайт/с Кбайт Кбайт

таким образом, ответ – 3750 Кбайт.

Телекоммуникационные технологии.

Задача 2. Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,2 2) 2 3) 3 4) 4

Решение:

А) так как частота дискретизации 16 кГц, за одну секунду запоминается 16000 значений сигнала

Б) так как глубина кодирования – 24 бита = 3 байта, для хранения 1 секунды записи требуется 16000  3 байта = 48 000 байт

(для стерео записи – в 2 раза больше)

В) на 1 минуту = 60 секунд записи потребуется

60  48000 байта = 2 880 000 байт, то есть около 3 Мбайт

Таким образом, правильный ответ – 3.

Технология программирования.

Выводы:

• Тесты ЕГЭ охватывают все пункты базового курса «Информатика и ИКТ»
• Во всех заданиях тестов ЕГЭ по информатике и ИКТ присутствует межпредметная связь, т.к. информационные технологии затрагивают все области наук.
• В ходе работы над проектом, замечено, что некоторые задания (исполнитель робот, количество решений логических уравнений, задачи на перебор вариантов и т.д.) содержат большой объем обрабатываемой информации и громоздкий алгоритм решения, что отрицательно сказывается в резу льтатах ЕГЭ.

Заключение:

• Необходимо упростить некоторые задачи ЕГЭ, забирающие много времени, отводимой для выполнения теста ЕГЭ.
• Уменьшить количество заданий А и В.
• Связать (учебники) программу курса «Информатика и ИКТ» с тестами заданий ЕГЭ.

Поставленные вопросы являются темами следующих проектных работ.

Литература.

1. Единый государственный экзамен: информатика: контроль. Измерит. Материалы:2009. – М.: Просвещение, СПб.: филиал изд-ва «Просвещение», 2009.-176 с.

2. Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/Под редакцией В.Р. Лещинера /ФИПИ. –М:Интеллект-Центр,2009 – 136 с.

4. Гусева И.Ю. ЕГЭ. Информатика: Раздаточный материал тренировочных тестов. – СПб.:Тритон,2009 – 120 с.

5. Самылкина Н.Н., Островская Е.М. ЕГЭ 2010. Информатика: Тренировочные задания. – М.: Эксмо, 2009 – 208 с.