«Некоторые приёмы решения квадратных уравнений»
Автор доклада: Мащалгина Татьяна Васильевна,
учитель математики МБОУ «Верхне – Устькулойская
основная школа № 24» д. Мелединская,
Вельского района Архангельской области
Согласно программе по математике уравнения изучаются с 1 по 11 классы. Материал, связанный с уравнениями, составляет значительную часть школьного курса математики. В 7 – 9 классах на уроках алгебры на изучение уравнений отводится примерно 20% учебного времени. Это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.[2]
Уравнения – это язык алгебры. Квадратные уравнения – это фундамент, на котором построено здание алгебры.
В школьном курсе алгебры изучаются формулы корней квадратного уравнения, с помощью которых можно решать любые квадратные уравнения. Но имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать данные уравнения. Эти приёмы не отражены в школьных учебниках математики, но овладение ими поможет ученикам в дальнейшем экономить время при решении текстовых задач, квадратных неравенств, тригонометрических, логарифмических и показательных уравнений.
Цель доклада: показать наиболее удобные и интересные приёмы решения квадратных уравнений для восьмиклассников и учителей; развивать сообразительность; воспитывать интерес к предмету.
Ещё в Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так учёный человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто излагали в стихотворной форме.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары:
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая.
Сколько ж было обезьянок
Ты скажи мне, в этой стае?[4]
В «Арифметике» Диофанта содержится ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Решая задачу «Найти два числа, зная, что их сумма равна 20, а произведение - 96», Диофант рассуждает так: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 - х. Разность между ними 2х.
(10 + х)(10 - х) = 96, 100 - х2 = 96, х2 - 4 = 0 , Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.[3]
Итальянские математики Тарталья, Кардано, Бомбелли первыми в XVI в. учитывают, кроме положительных, и отрицательные корни. Лишь в XVII в. благодаря труду Жирара, Декарта, Ньютона способ решения квадратных уравнений принимает современный вид.
К изучению данной темы современные школьники приступают в 8 классе. Определение квадратного уравнения даётся практически одинаково всеми авторами учебников алгебры: «Квадратным уравнением называется уравнение вида ах2 + bx + c = 0, где х – переменная, а, b и с – любые действительные числа, причём а ≠ 0». [1]
Ввести данное понятие можно разными методами. Например, Алимов Ш.А. использует для введения текстовую задачу «Основание прямоугольника больше высоты на 10 см, а его площадь равна 24 см2. Найдите высоту прямоугольника». Мордкович А.Г. вводит определение, но заранее знакомит с пятью способами графического решения квадратных уравнений.[1]
Сначала обучающиеся учатся решать неполные квадратные уравнения, т.к. для этого не приходится изобретать ничего нового. Такие уравнения бывают трёх видов.
Таблица 1.
| ах2 + bx = 0 х(ах + b) = 0 х1 = 0; ах + b = 0 х2 =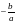
| ах2 + c = 0 ах2 = – c х2 = – х1 = ; х2 = - ; х2 = - | ах2 = 0 х = 0 |
| 2х2 + 5x = 0 x – 6х2 = 0 | 5х2 – 45 = 0 3х2 + 27 = 0 (корней нет) | 7х2 = 0 0,3х2 = 0 |
Затем решаются уравнения с помощью разложения квадратного трёхчлена на множители способом группировки и методом выделения полного квадрата. Но данный способ требует хорошей математической подготовки обучающихся.
Универсальным способом, пригодным для решения любых квадратных уравнений, считают решение по формуле
х1,2 = 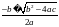 (1)
(1)
Если окажется, что дискриминант D = b2 – 4ас - отрицательное число, то корней нет; если D = 0, то один корень х =  ; если D – положительное число, то уравнение имеет два корня (1).
; если D – положительное число, то уравнение имеет два корня (1).
Чтобы облегчить вычисления, необходимо показать формулу для вычисления корней квадратного уравнения, если коэффициент b является чётным числом. У восьмиклассников появляется свобода выбора.
Если коэффициентами квадратного уравнения являются обыкновенные дроби, показываем, как освободиться от знаменателей, умножая обе части уравнения на наименьший общий знаменатель.
Если же коэффициентами являются десятичные дроби, то разумно умножить обе части уравнения на 10, 100 и т.д.
Приведённые квадратные уравнения (а = 1) учим решать с помощью теоремы Виета и теоремы, обратной теореме Виета.
Необходимо показать применение метода введения новой переменной как при решении биквадратного уравнения, так и при решении уравнений с повторяющимся дважды множителем.
Например: (х2 + 2х)2 – 2(х2 + 2х) – 3 = 0
х2 + 2х = а
а2 – 2а – 3 = 0
а1 = -1 а2 = 3
х2 + 2х = -1 х2 + 2х = 3
х2 + 2х + 1 = 0 х2 + 2х – 3 = 0
х1 = - 1 х2 = 1 х3 = -3
Ответ: -3; -1; 1.
После того, как обучающиеся овладели алгоритмом решения квадратных уравнений, знакомлю с некоторыми интересными приёмами, основанными на свойствах коэффициентов квадратного уравнения. Для основной школы использую шесть приёмов.
I.Если а + b + с = 0, то х1 = 1, х2 =  .
.
Например: 5х2 – 2x – 3 = 0 (Ответ: 1; -0,6)
4х2 – 5x + 1 = 0 (Ответ: 1; 0,25)
2х2 + 7x – 9 = 0 (Ответ: 1; -4,5)
II.Если а + с = b, то х1 = -1, х2 = -  .
.
Например: 5х2 + 11x + 6 = 0 (Ответ: -1; -1,2)
х2 – 9x – 10 = 0 (Ответ: -1; 10)
2х2 – 7x – 9 = 0 (Ответ: -1; 4,5)
III.Если ах2 + (а2 + 1)x + а = 0, то х1 = – а, х2 = – .
.
Например: 6х2 + 37x + 6 = 0 (Ответ: – 6; – )
)
4х2 + 17x + 4 = 0 (Ответ: – 4; –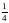 )
)
15х2 + 226x + 15 = 0 (Ответ: – 15; – )
)
IV.Если ах2 + (а2 – 1)x – а = 0, то х1 = – а, х2 =  .
.
Например: 3х2 + 8x – 3 = 0 (Ответ: – 3;  )
)
10х2 + 99x – 10 = 0 (Ответ: – 10; 0,1)
17х2 + 288x – 17 = 0 (Ответ: – 17;  )
)
V. Если ах2 – (а2 + 1)x + а = 0, то х1 = а, х2 =  .
.
Например: 2х2 – 5x + 2 = 0 (Ответ: 2;  )
)
4х2 – 17x + 4 = 0 (Ответ: 4; 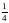 )
)
12х2 – 145x + 12 = 0 (Ответ: 12;  )
)
VI. Если ах2 – (а2 – 1)x – а = 0, то х1 = а, х2 = – .
.
Например: 5х2 – 24x – 5 = 0 (Ответ: 5; – )
)
10х2 – 99x – 10 = 0 (Ответ: 10; – 0,1)
30х2 – 899x – 30 = 0 (Ответ: 30; – )
)
При многократном использовании вышеперечисленных приёмов добиваюсь заучивания первых двух и применения остальных с помощью памятки.
С целью развития внимания и сообразительности составляем с восьмиклассниками таблицу зависимости знаков корней от знаков коэффициентов.
Таблица 2.
| Знаки коэффициентов | Знаки корней |
| а 0, b 0, с 0 | Оба отрицательные |
| а 0, b 0 | Оба положительные |
| а 0, b 0, с | Больший по модулю отрицательный |
| а 0, b | Больший по модулю положительный |
Например: составить квадратное уравнение, если х1 = 2, х2 = – 5.
Решение: а 0, b 0, с
b = –(2 – 5) = 3, с = 2 ∙ (–5) = –10
Ответ: х2 + 3x – 10 = 0
Все мы умеем решать квадратные уравнения со школьной скамьи. Эти уравнения в дальнейшем находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств.
Самым главным в решении квадратных уравнений является рационально выбранный приём решения. Так как эти приёмы решения квадратных уравнений просты в применении, то они, безусловно, должны заинтересовать увлекающихся математикой учеников, помочь эффективно решать уравнения, уменьшая затраты времени.






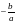

 ; х2 = -
; х2 = -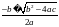 (1)
(1)  ; если D – положительное число, то уравнение имеет два корня (1).
; если D – положительное число, то уравнение имеет два корня (1). .
. )
)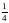 )
) )
) )
) )
) )
) )
) )
) )
)

















