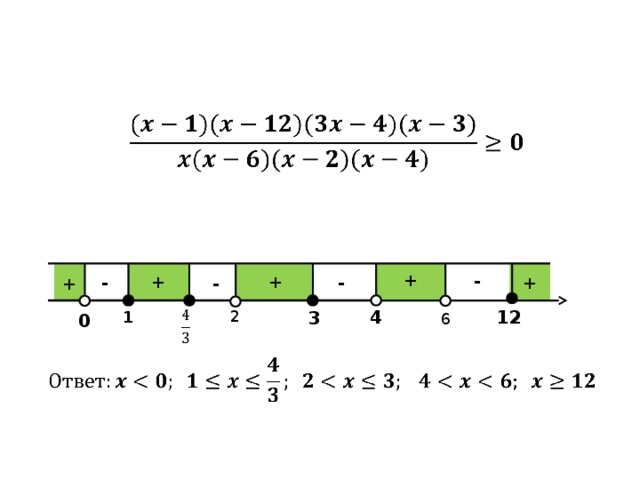Россия, Железногорск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 20.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 14.05.2025 07:51
Бородкина Татьяна Ивановна
учитель математики
54 года
6 243
8 023 
Местоположение
Специализация
Применение метода рационализации для решения неравенств.
Категория:
Алгебра
02.07.2018 11:19
Просмотр содержимого документа
«Применение метода рационализации для решения неравенств.»
Муниципальное общеобразовательное учреждение «Гимназия№1»
Применение метода рационализации для решения неравенств
Учитель математики
Бородкина Т.И
Г. Железногорск
2017
Метод рационализации ( метод замены множителей, метод замены функции, правило знаков) позволяет перейти от неравенства, содержащего сложные показательные, логарифмические и т.п выражения, к равносильному ему более простому рациональному неравенству на области определения исходного неравенства
Метод рационализации
- Есть неравенства вида
где , - константы или выражения, зависящие от x
- Каждый из множителей заменяем на совпадающий с ним по знаку
0 При h1 знак - совпадает со знаком При hСледовательно, при всех значениях совпадает со знаком . " width="640"
Замена множителей на примере -
Есть множитель - где h0
- При h1 знак - совпадает со знаком
- При h
- Следовательно, при всех значениях совпадает со знаком .
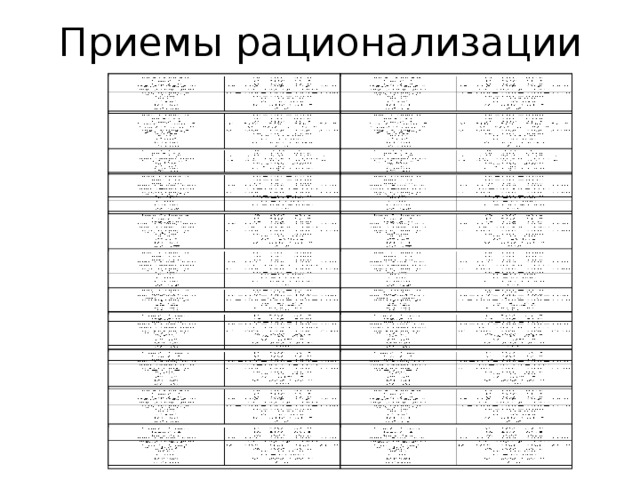
Приемы рационализации
0
1
0
0
0
0
0
0
( 0
0
1
*h 0
0
Где f 0, g 0, h1,p 0,p f, g - функции от х h, p - функция или число - один из знаков , , , и обязательно учитываем ОДЗ исходного неравенства
Решите неравенство:
0
Решение:
-
-
+
+
-5
-6
1
x
x
-1
-7
1
Ответ: -7;-6) -5,-1 ; x=1
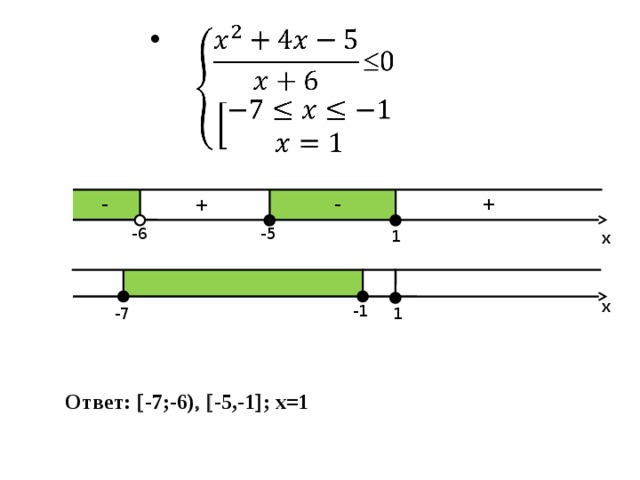
Решите неравенство:
Решение:
-
-
x
3
-1
4
x
8
-2
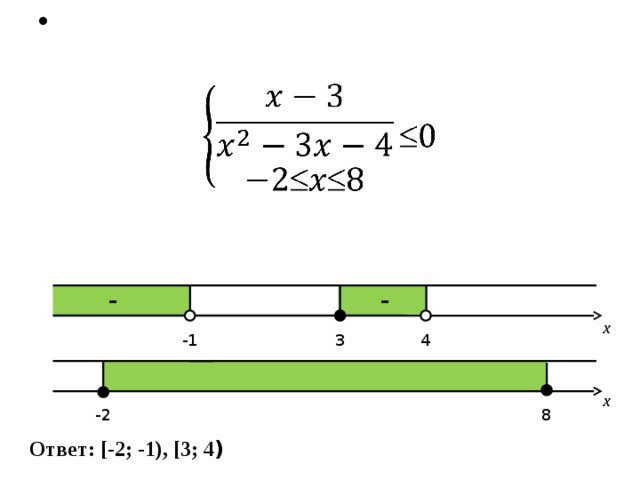
Ответ: [-2; -1), [3; 4 )
Решите неравенство:
Решение:
При , тогда
-
+
+
-
+
+
-
x
-5
-3
-2
0,5
1
3
x
7
-5
Ответ: x=-5
-3
0,5
3
Решите неравенство:
Решение:
+
-
+
+
-
-
+
+
-
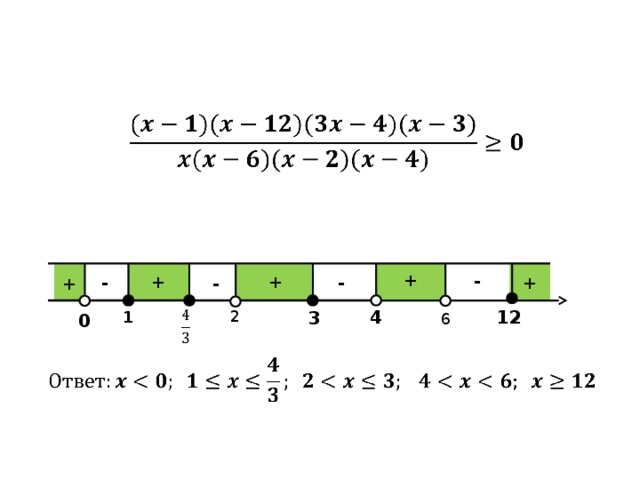
12
4
2
3
1
6
0
Решите неравенство:
1
Решение:
ОДЗ:
t
t
x+1
x -1
x
Используя метод рационализации, получим:
x(x-1) 0
x 0
Ещё раз рационализируем:
(2-1)(x+1)x(x-1) 0
(x+1)x(x-1) 0
Ответ: -1 x 0; x 1
Решите неравенство:
Решение:
Применяя метод замены множителей:
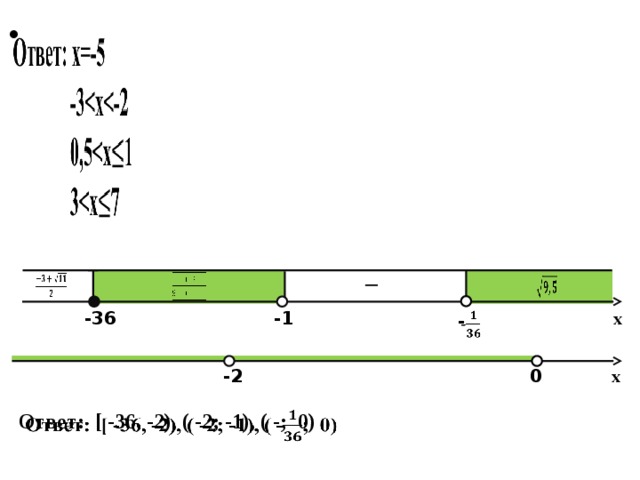
x
-1
-36
-
x
-2
0
Ответ: [ -36, -2), ( -2; -1), ( -; 0)
Решите неравенство:
Решение:
x=6 удовлетворяет неравенству
1
Пусть
=
Так как
- это знак
При исходное неравенство примет вид :
, где ;
Используя рационализацию, получим:
+
+
-
+
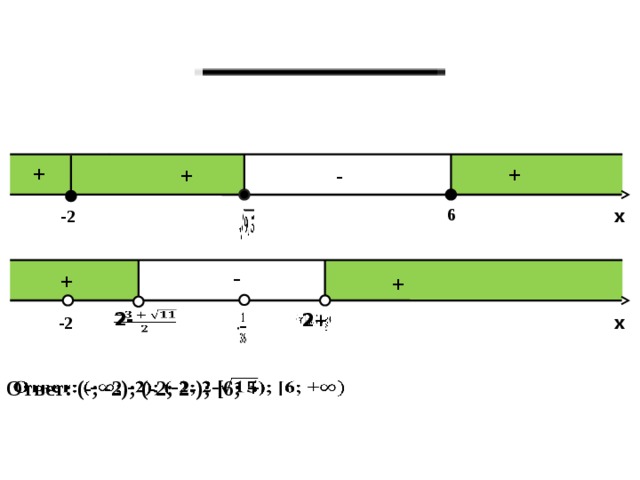
6
-2
x
-
+
+
2-
2+
-2
x
Ответ: (-; -2); (-2; 2-); [6; +
МГУ(Экономический факультет),2013г решите неравенство
Решение:
Пусть = t
0
Разложим на множители 2
t = 3 2*27-19*3+3=0 верно
По схеме Горнера
2
2
=3
0
0
2
2
-19
-19
6
6
-1
3
3
-1
0
0
t
0
3
t
0
3
- или 3
- 3
1
-2 2
2
Ответ: ,
Решите неравенство:
-8-
Решение:
=a
a-8-
a-8
a-8
a-8
a-8, где a
0 , a
0 , a
Обратная замена и замена множителей:
0 ,
0 , x
0 , x
0 , x
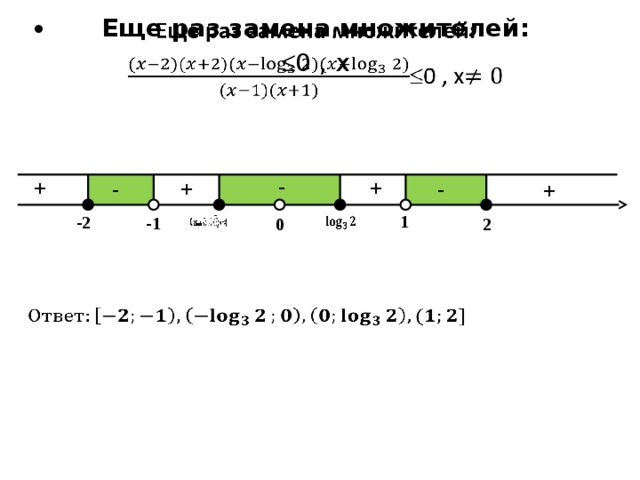
Еще раз замена множителей:
0 , x
-
+
+
-
-
+
+
1
-2
-1
0
2
-
Спасибо за внимание!
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
