Применение производной к исследованию функции

Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство f ! (х)≥0 (причем равенство f ! (х)=0 выполняется лишь в изолированных точках), то функция у= f (х) возрастает на промежутке Х.

Теорема 2. Если во всех точках открытого промежутка Х выполняется неравенство f ! (х)≤0 (причем равенство f ! (х)=0 выполняется лишь в изолированных точках), то функция у= f (х) убывает на промежутке Х.

Теорема 3. Если во всех точках открытого промежутка Х выполняется равенство f ! (х)=0,то функция у= f (х) постоянна на промежутке Х.

3

Пример: Исследовать на монотонность функцию у=2х 3 +3х 2 – 1.

Исследовать функцию на монотонность – это значит выяснить, на каких промежутках области определения функция возрастает, а на каких – убывает. Согласно теоремам 1 и 2, это связано со знаком производной.

Найдем производную данной функции:

f ! (х)=6х 2 +6х=6х (х+1)

f ! (х)

+

+

х

0

-1

f (х)

Если функция непрерывна не только на открытом промежутке, но и в его концевых точках (именно так обстоит дело для заданной функции), эти концевые точки включают в промежуток монотонности функции.

Ответ: функция возрастает хЄ(-∞; - 1 ] , [0 ; + ∞), функция убывает хЄ [ -1 ; 0]

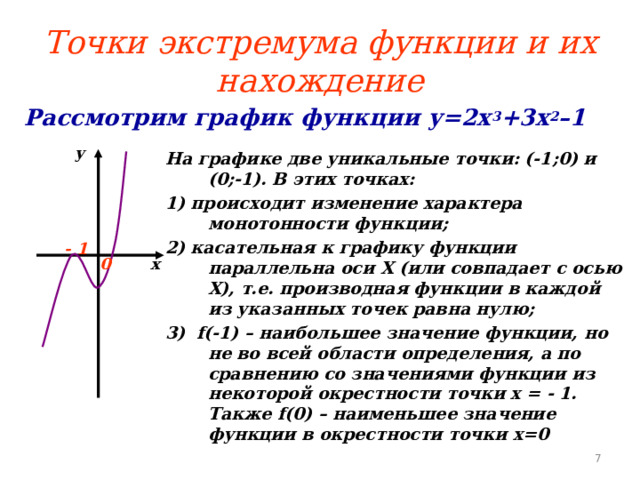
Точки экстремума функции и их нахождение

Рассмотрим график функции у=2х 3 +3х 2 –1

у

На графике две уникальные точки: (-1;0) и (0;-1). В этих точках:

1) происходит изменение характера монотонности функции;

2) касательная к графику функции параллельна оси Х (или совпадает с осью Х), т.е. производная функции в каждой из указанных точек равна нулю;

3) f(-1) – наибольшее значение функции, но не во всей области определения, а по сравнению со значениями функции из некоторой окрестности точки х = - 1. Также f (0) – наименьшее значение функции в окрестности точки х=0

- 1

х

0

f (х 0 ) . Определение 2. Точку х=х 0 называют точкой максимума функции у = f (х) , если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х 0 ) выполняется неравенство f (х) f (х 0 ) . " width="640"

Определение 1 . Точку х=х 0 называют точкой минимума функции у = f (х) , если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х 0 ) выполняется неравенство

f (х) f (х 0 ) .

Определение 2. Точку х=х 0 называют точкой максимума функции у = f (х) , если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х 0 ) выполняется неравенство

f (х) f (х 0 ) .

Значение максимума и минимума обозначаются: у max , y min соответственно.

ВНИМАНИЕ!!!

Только не путать с наибольшим (или наименьшим) значением функции во всей рассматриваемой области определения, эти значения в окрестности некоторой точки Х, являются наибольшими (или наименьшими).

Точки минимума и максимума функции называют – точки экстремума (от латинского слова extremum – «крайний»)

Теорема 4 . Если функция у = f (х) имеет экстремум в точке х=х 0 , то этой точке производная либо равна нулю, либо не существует.

Внутренние точки области определения функции, в которых производная функции равна нулю, называют стационарными , а внутренние точки области определения функции, в которых функция непрерывна, но производная не существует – критическими .

х 0 – неравенство f 1 (x) 0, то х=х 0 – точка минимума функции у= f(x) ; 2) Если у этой точки существует такая окрестность, в которой при х х 0 выполняется неравенство f 1 (x) 0 , а при х х 0 – неравенство f 1 (x) , то х=х 0 – точка максимума функции у= f(x) ; 3) Если у этой точки существует такая окрестность, что в ней и слева и справа от точки х 0 знаки производной одинаковы, то в точке х 0 экстремума нет. " width="640"

Теорема 5 (достаточные условия экстремума) . Пусть функция у = f (х) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х=х 0 .Тогда:

1) Если у этой точки существует такая окрестность, в которой при х х 0 , выполняется неравенство f 1 (x) , при х х 0 – неравенство f 1 (x) 0, то х=х 0 – точка минимума функции у= f(x) ;

2) Если у этой точки существует такая окрестность, в которой при х х 0 выполняется неравенство f 1 (x) 0 , а при х х 0 – неравенство f 1 (x) , то х=х 0 – точка максимума функции у= f(x) ;

3) Если у этой точки существует такая окрестность, что в ней и слева и справа от точки х 0 знаки производной одинаковы, то в точке х 0 экстремума нет.

Для запоминания!!!

min

max

Экстремума нет

Экстремума нет

Пример: Найти точки экстремума функции у=3х 4 – 16х 3 + 24х 2 – 11.

Решение: найдем производную данной функции: у 1 =12х 3 – 48х 2 + 48х.

Найдем стационарные точки:

12х 3 – 48х 2 + 48х=0

12х(х 2 – 4х + 4)=0

12х(х – 2) 2 =0

Производная обращается в нуль в точках х=0 и х=2

-

+

+

2

х

0

Значит, х=0 – точка минимума.

Ответ: у min = - 11 .

• Алгоритм исследования непрерывной функции у= f (х) на монотонность и экстремумы:

• Найти производную f 1 (х).
• Найти стационарные ( f 1 (х)=0) и критические ( f 1 (х) не существует) точки функции у= f (х).
• Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
• На основании теорем 1, 2, и 5 сделать выводы о монотонности функции и о ее точках экстремума.

Пример: Исследовать функцию на монотонность и экстремумы

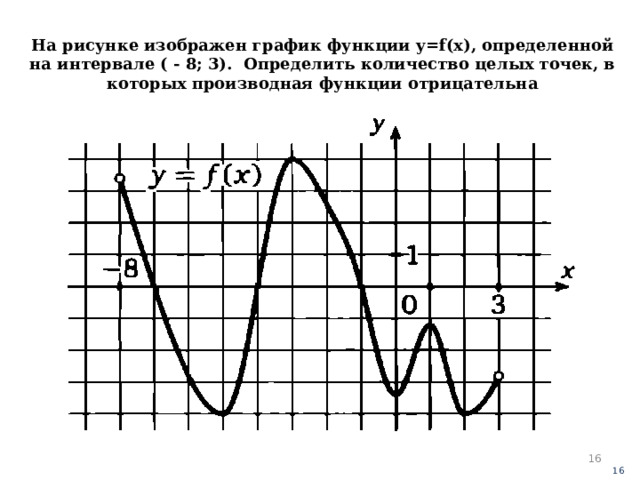
На рисунке изображен график функции y=f(x) , определенной на интервале ( - 8; 3). Определить количество целых точек, в которых производная функции отрицательна

Ответ: 4

На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 7; 5). Найти точку экстремума функции на отрезке [ -6 ; 4]

Ответ: - 3

На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 3; 8). Найти количество точек максимума функции на отрезке [ - 2 ; 7 ]

Ответ: 2

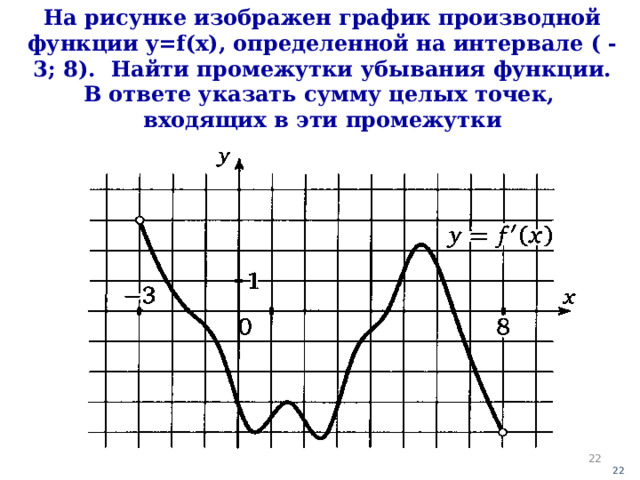
На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 3; 8). Найти промежутки убывания функции. В ответе указать сумму целых точек, входящих в эти промежутки

Ответ: 16

На рисунке изображен график производной функции y=f(x) , определенной на интервале ( - 11; 3). Найти промежутки возрастания функции. В ответе указать длину наибольшего из них

Ответ: 6

Литература :

• Мордкович, А. Г., Семенов, П. В., Алгебра и начала математического анализа, геометрия. 10 класс, часть 1, учебник - Москва, изд. «Мнемозина», 2020г.–455с.
• 2. Мордкович, А. Г., Семенов, П. В., Алгебра и начала математического анализа, геометрия. 10 класс, часть 2, задачник - Москва, изд. «Мнемозина», 2020г.–351с.