Применение законов динамики

Применение законов динамики

Практикум по решению задач на применение законов Ньютона

Алгоритм решения задач на применение законов динамики

• Записать данные, перевести их в систему СИ.
• Сделать чертеж, указать направление ускорения и скорости, действующих сил, координатные оси.
• Записать 2 закон Ньютона в векторной форме и в проекциях на оси ОХ и ОУ.
• Записать дополнительные необходимые законы, выполнить преобразования.
• Произвести вычисления, записать ответ.

1.1. Движение по горизонтали

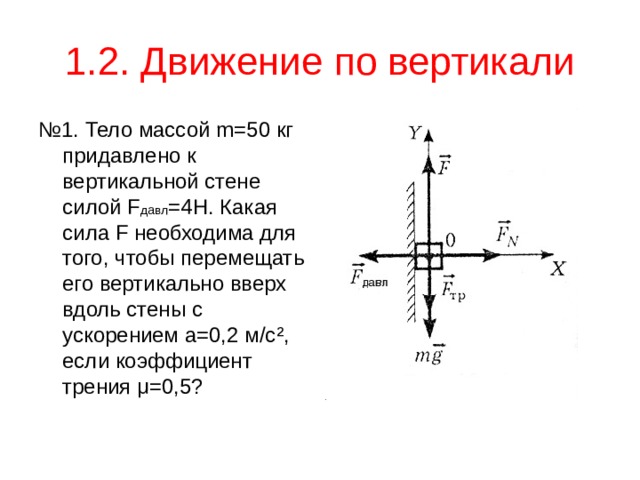
1.2. Движение по вертикали

№ 1. Тело массой m =50 кг придавлено к вертикальной стене силой F давл =4Н. Какая сила F необходима для того, чтобы перемещать его вертикально вверх вдоль стены с ускорением a =0,2 м/с ² , если коэффициент трения μ =0,5?

1.2. Движение по вертикали

• В векторном виде: …..
• В проекциях на оси ОХ и ОУ:

ОХ: 0= F N –F давл или F N = F давл

ОУ: ma= F - mg – F тр

• Преобразования: F = m ( a+g ) + F тр

F тр = μ F N или окончательно

4. F = m ( a+g ) + μ F N

5. Вычисления: F =502 Н

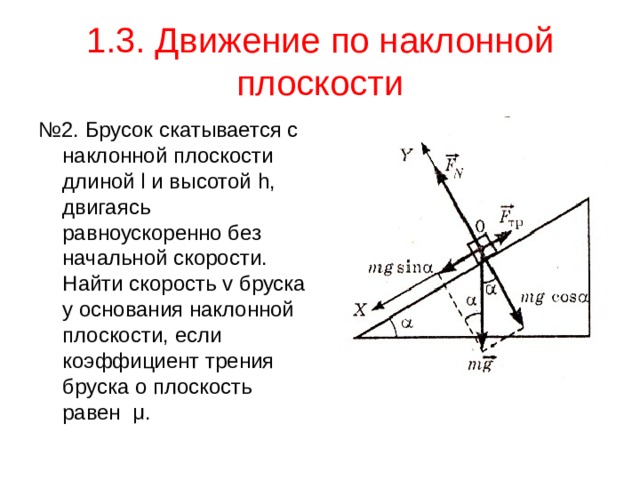
1.3. Движение по наклонной плоскости

№ 2. Брусок скатывается с наклонной плоскости длиной l и высотой h , двигаясь равноускоренно без начальной скорости. Найти скорость v бруска у основания наклонной плоскости, если коэффициент трения бруска о плоскость равен μ .

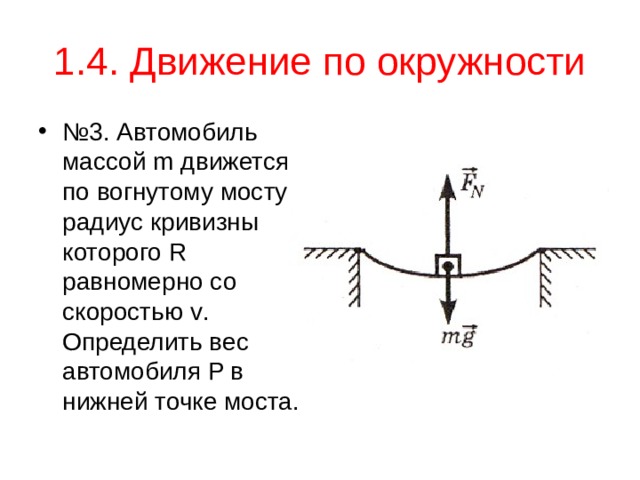
1.4. Движение по окружности

• № 3. Автомобиль массой m движется по вогнутому мосту радиус кривизны которого R равномерно со скоростью v . Определить вес автомобиля P в нижней точке моста.

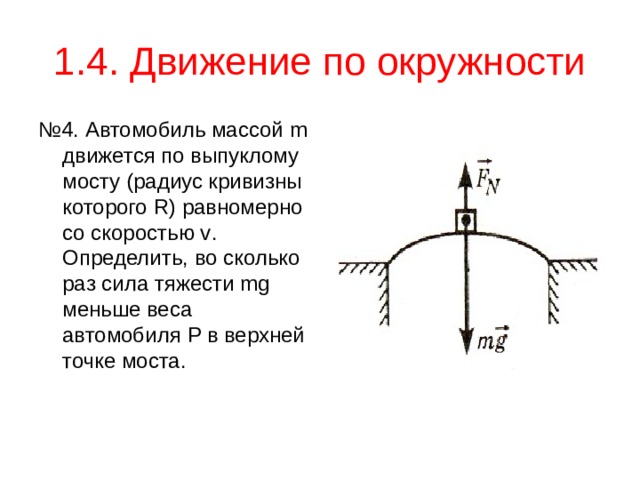
1.4. Движение по окружности

№ 4 . Автомобиль массой m движется по выпуклому мосту (радиус кривизны которого R ) равномерно со скоростью v . Определить, во сколько раз сила тяжести mg меньше веса автомобиля P в верхней точке моста.

1.4. Движение по окружности

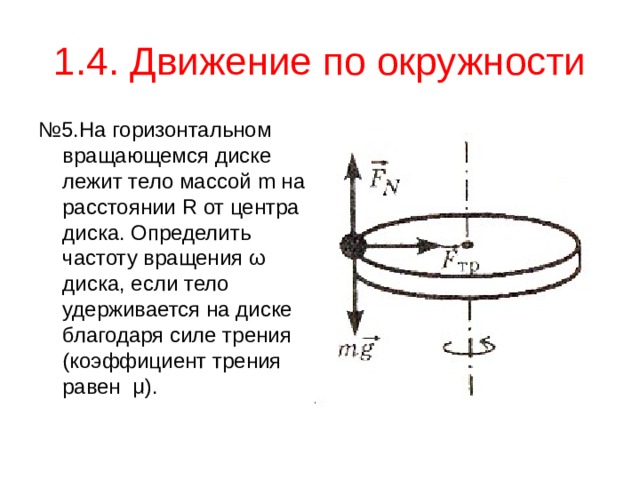
№ 5.На горизонтальном вращающемся диске лежит тело массой m на расстоянии R от центра диска. Определить частоту вращения ω диска, если тело удерживается на диске благодаря силе трения (коэффициент трения равен μ ).

1.4. Движение по окружности

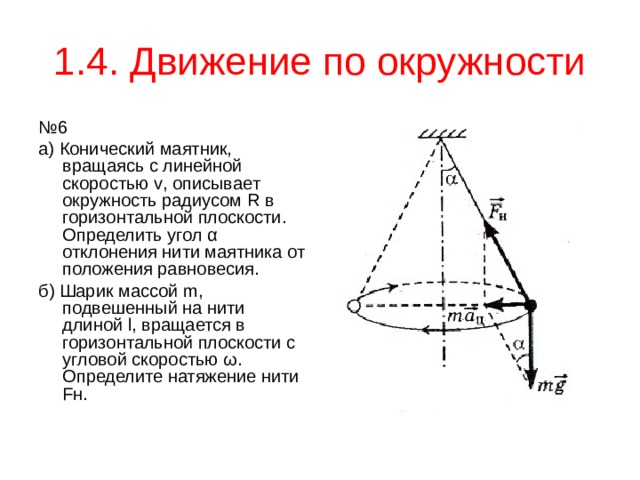
№ 6

а) Конический маятник, вращаясь с линейной скоростью v , описывает окружность радиусом R в горизонтальной плоскости. Определить угол α отклонения нити маятника от положения равновесия.

б) Шарик массой m , подвешенный на нити длиной l , вращается в горизонтальной плоскости с угловой скоростью ω . Определите натяжение нити F н.