Принцип Дирихле

Приведу еще похожее на принцип Дирихле (и столь же очевидное) утверждение, взятое из литературы и используемое мною при решении аналитических задачах:

3* «Если среднее арифметическое нескольких чисел больше А, то хотя бы одно из этих чисел больше А».

Например : Возьмем числа: 2, 3, 4. Их среднее арифметическое (2 + 3 + 4) : 3 = 3 2 и 4 2.

n то, по крайней мере, в одной части будет более одного элемента» 5* . «Предположим, m зайцев рассажены в n клетках. Тогда, если m n , то хотя бы в одной клетке содержится не менее m:n зайцев, а также хотя бы в одной другой клетке содержится не более m:n зайцев». " width="640"

Обобщенный принцип Дирихле

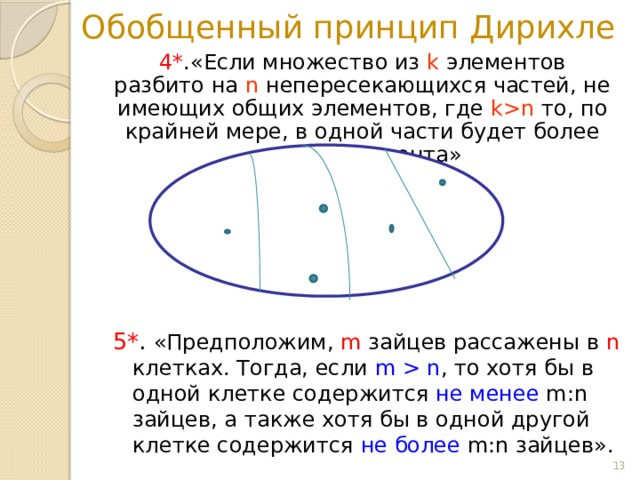
4* .«Если множество из k элементов разбито на n непересекающихся частей, не имеющих общих элементов, где kn то, по крайней мере, в одной части будет более одного элемента»

5* . «Предположим, m зайцев рассажены в n клетках. Тогда, если m n , то хотя бы в одной клетке содержится не менее m:n зайцев, а также хотя бы в одной другой клетке содержится не более m:n зайцев».

12, то, по принципу Дирихле (формулировка 1* ) найдется, как минимум, одна «клетка», в которой будет сидеть, по крайней мере, 2 «зайца». Ответ: найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса. " width="640"

Задачи и их решение

1. В классе 15 учеников. Доказать, что найдутся как минимум 2 ученика, отмечающих дни рождения в один месяц.

Решение:

Пусть 15 учеников будут «зайцы». Тогда «клетками» будут месяцы года, их 12. Так как 1512, то, по принципу Дирихле (формулировка 1* ) найдется, как минимум, одна «клетка», в которой будет сидеть, по крайней мере, 2 «зайца».

Ответ: найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса.

2. В ковре размером 3х3 метра Коля

проделал 8 дырок. Доказать, что из него можно вырезать коврик размером 1х1 метр, не содержащий внутри себя дырок.

Решение:

Разрежем ковер на 9 ковриков размерами 1х1 метр, Так как ковриков - «клеток» - 9, а дырок - «голубей» - 8, то по принципу Дирихле (формулировка 2* ) делаем вывод.

Ответ: найдется коврик размером 1х1м без дырок внутри.

4, значит по формулировке 3* найдется школьник, знающий не менее 5 стихотворений. 2 способ : предположим, что каждый школьник знает не более 4 стихотворений. Значит, 27 школьников знают не более 4•27=108(стихотворений), значит найдется школьник, знающий не менее 5 стихотворений. 3 способ : 27 школьников – это клетки, 109 стихов – это зайцы, 109 27, по принципу Дирихле ( 5 * ) хотя бы в одной клетке содержится не менее 109 : 27 = 4 зайцев, то есть не менее 5. Ответ: значит найдется школьник, знающий не менее 5 стихотворений. " width="640"

3. В 3а классе учится 27 школьников, знающих

всего 109 стихотворений. Доказать, что найдется

школьник, знающий не менее 5 стихотворений.

Решение:

1 способ : узнаем, сколько стихотворений в среднем знает каждый ученик 3а класса: 109 : 27 = 4 4, значит по формулировке 3* найдется школьник, знающий не менее 5 стихотворений.

2 способ : предположим, что каждый школьник знает не более 4 стихотворений. Значит, 27 школьников знают не более 4•27=108(стихотворений), значит найдется школьник, знающий не менее 5 стихотворений.

3 способ : 27 школьников – это клетки, 109 стихов – это зайцы, 109 27, по принципу Дирихле ( 5 * ) хотя бы в одной клетке содержится не менее 109 : 27 = 4 зайцев, то есть не менее 5.

Ответ: значит найдется школьник, знающий не менее 5 стихотворений.

4. В городе 15 школ. В них обучается 6015

школьников. В концертном зале городского Дворца

культуры 400 мест. Доказать, что найдётся школа,

ученики которой не поместятся в этот зал.

Решение:

Эту задачу также можно решить несколькими способами. Я буду использовать принцип 3*. Найду среднее количество школьников в каждой школе 6015 : 15 = 401, значит найдется школа, в которой более 401 ученика.

Ответ:

Поэтому ученики какой-то школы не поместятся в зал на 400 мест.

5. В школе 5 восьмых классов: 8а, …, 8д. В каждом из них учится по 32 человека. Доказать, что найдутся 14 человек, родившихся в одном месяце.

Решение:

1 способ: предположим, что в каждом месяце родилось не более 13 учеников. Значит за 12 месяцев родилось 12•13=156(школьников).

Но по условию в школе обучается 5•32=160(человек). Значит, найдется месяц, в котором родилось больше, чем 13 учеников, то есть хотя бы 14.

2 способ: ученики, их 5•32=160(человек) – «кролики», 12 месяцев – «клетки», применяем принцип 5* , то хотя бы в одной «клетке» не менее

160 : 12 = 13,33… «зайцев», т.е. хотя бы 14.

Ответ:

Значит, найдется месяц, в котором родилось больше, чем 13 учеников, то есть хотя бы 14.

6. Задача на комбинаторику В коробке лежат шарики 4-х разных цветов (много белых, много черных, много синих, много красных). Какое наименьшее количество шариков надо на ощупь вынуть из мешка, чтобы среди них заведомо оказались два одного цвета?

Решение

Эта задача изумительно решается с помощью принципа 1*

Возьмем за «кроликов» шары, а за «клетки» - черный, белый, синий, красный цвета. Клеток 4, поэтому если кроликов, хотя бы 5, то какие-то два попадут в одну клетку (будет 2 одноцветных шарика).

Ответ: наименьшее количество – 5 шариков

7. Доказать, что среди шести целых чисел найдутся два числа, разность которых делится на 5.

Решение.  Рассмотрим множество из 6 элементов, разобьем его на 5 непересекающихся частей, пронумерованных 0,1,2,3,4, - цифрами, представляющими собой остатки от деления на 5. Распределим в эти 5 частей шесть произвольных целых чисел в соответствии с остатком от деления на 5, то есть, в одну и ту же часть помещаем числа, имеющие одинаковый остаток от деления на 5. Поскольку элементов больше, чем частей, согласно принципу 4* , существует по крайней мере одна часть, содержащая более одного элемента. Следовательно, существуют два числа с одинаковым остатком от деления на 5. Тогда, разность этих чисел делится на 5.

8. В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежат яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?

Решение:

Задачи для самостоятельного решения

9. Доказать, что среди 101 целого числа всегда можно выбрать два таких, что их разность делится на 100.

10. В классе 30 человек. Саша Иванов в диктанте сделал 13 ошибок, а остальные – меньше. Доказать, что по крайней мере 3 ученика сделали ошибок поровну (может быть, по 0 ошибок).

11. Шесть школьников съели семь конфет. Доказать, что один из них съел не мене двух конфет.

12. У человека на голове не более 400 000 волос, в Москве более 8 миллионов жителей. Доказать, что найдутся 20 москвичей с одинаковым числом волос.

13. Петя хочет написать на доске 55 различных двузначных чисел так, чтобы среди них не было двух чисел, дающих в сумме 100. Сможет ли он это сделать?

Вывод

• Я поняла, что принцип Дирихле важен, интересен, полезен. Его можно применять в повседневной жизни, что развивает логическое мышление.
• Многие олимпиадные задачи решаются c помощью этого специального принципа. Он дает возможность обобщать.
• Меня поразила совершенная очевидность этого принципа. Его применение является весьма эффективным методом решения задач, дающим во многих случаях наиболее простое и изящное решение.
• Я узнала, чтобы применять данный метод, надо:

определить, что удобно в задаче принять за «клетки», а что за «кроликов»;

выбрать для решения требуемую формулировку принципа Дирихле.

Вывод

• Я изучила принцип Дирихле и умею решать некоторые пока не сложные олимпиадные задачи с помощью разных формулировок этого принципа
• В дальнейшем я планирую применять этот принцип для решения более сложных олимпиадных задач
• Обязательно выступлю перед своими одноклассниками и научу их решать олимпиадные задачи по принципу Дирихле

Используемая литература

• В.А.Гусев, А.И.Орлов, А.П.Розенталь «Внеклассная работа по математике в 6-8 классах», М: Просвещение – 1984, (принцип Дирихле с.67-78)
• В.В.Прасолов, Задачи по планиметрии, ч.2, Москва, Наука, 1991, 139стр.
• И.Л.Бабинская, Задачи математических олимпиад, Москва, Наука, 1975, 112стр.
• А.В. Спивак "Математический праздник", М.:МЦНМО, 1995 - 78стр. (пр.Дирихле 62-66)
• С.А. Генкин, И.В. Итенберг, Д.В. Фомин "Ленинградские математические кружки", 1994 - 272стр. (пр.Дирихле 39-47)
• А.Я. Канель-Белов, А.К. Ковальджи "Как решают нестандартные задачи", М.:МЦНМО, 1997 - 96стр. (пр.Дирихле 29-32)
• Задачи для внеклассной работы по математике в 5-6 классах/ сост.В.Ю. Сафонова, М.:МИРОС, 1995 - 72стр. (пр.Дирихле 14-15)
•   Задачник Кванта: Математика. Часть 3./под ред.Н.Б.Васильева - 1997 - 128стр. (Шесть зайцев в пяти клетках В.Болтянский 16-22стр. (или в Квант, ╪2, 1977, 17-21стр.))
• http:// school-collection.edu.ru,
• http:// math.ru
• www.fcior.edu.ru

Спасибо

за внимание!