Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера

Б лаговещенский финансово-экономический колледж - филиал Финуниверситета

Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера

Автор-составитель:

Преподаватель информационных дисциплин

Ермихина М.А.

Благовещенск, 2017

План

• Принципы обработки информации компьютером.
• Арифметические и логические основы работы компьютера.

1. Принципы обработки информации компьютером

• Компьютер или ЭВМ (электронно-вычислительная машина) – это универсальное техническое средство для автоматической обработки информации
• Аппаратное обеспечение компьютера – это все устройства, входящие в его состав и обеспечивающие его исправную работу.

Не смотря на всё разнообразие компьютеров в современном мире, все они строятся по единой принципиальной схеме, основанной на фундаменте идеи программного управления Чарльза Бэббиджа (середина XIX в). Эта идея была реализована при создании первой ЭВМ ENIAC в 1946 г. коллективом ученых и инженеров под руководством Дж. фон Неймана

• Известный американский математик Джон фон Нейман сформулировал концепцию ЭВМ с водимыми в память программами и числами – программный принцип

Принципы фон Неймана

• Принцип двоичного кодирования. Для представления данных и команд используется двоичная система счисления.
• Принцип однородности памяти . Как программы (команды), так и данные хранятся в одной и той же памяти (и кодируются в одной и той же системе счисления — чаще всего двоичной). Над командами можно выполнять такие же действия, как и над данными.
• Принцип адресуемости памяти. Структурно основная память состоит из пронумерованных ячеек; процессору в произвольный момент времени доступна любая ячейка.

Принципы фон Неймана

• Принцип последовательного программного управления. Все команды располагаются в памяти и выполняются последовательно, одна после завершения другой.
• Принцип условного перехода. Команды из программы не всегда выполняются одна за другой. Возможно присутствие в программе команд условного перехода, которые изменяют последовательность выполнения команд в зависимости от значений данных. (Сам принцип был сформулирован задолго до Джона фон Неймана Адой Лавлейс и Чарльзом Бэббиджем, однако он логически включен в фон-неймановский набор как дополняющий предыдущий принцип.)

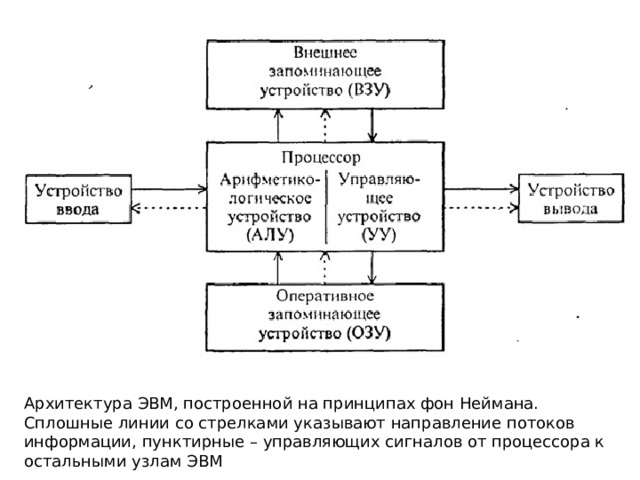
Архитектура ЭВМ, построенной на принципах фон Неймана. Сплошные линии со стрелками указывают направление потоков информации, пунктирные – управляющих сигналов от процессора к остальными узлам ЭВМ

2. Алгебра логики

- это раздел математики, возникший в XIX веке усилиями англ. математика Дж. Буля.

• Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в разработке различных электронных схем.
• Законы и аппарат алгебры логики стали использоваться при проектировании различных частей компьютеров (память, процессор)

Высказывания

• Алгебра логики оперирует высказываниями
• Высказывание – это повествовательное предложение, в отношении которого можно сказать: истинно оно или ложно.

Например:

• «Трава зеленая» – высказывание, оно истинно. «Солнце черное» – высказывание, оно ложно «Сходи за мелом» – не высказывание, это повелительное наклонение. «Хочешь кофе?» – не высказывание, вопросительное предложение.
• «Трава зеленая» – высказывание, оно истинно.
• «Солнце черное» – высказывание, оно ложно
• «Сходи за мелом» – не высказывание, это повелительное наклонение.
• «Хочешь кофе?» – не высказывание, вопросительное предложение.

Обозначение высказываний

• Высказывания обозначают большими латинскими буквами: A, B, C, D и т.д.
• Истинные высказывания равны 1 (А=1), ложные – 0 (А=0).

Например:

• Высказывание А: трава зеленая = 1, Высказывание В: солнце черное = 0
• Высказывание А: трава зеленая = 1,
• Высказывание В: солнце черное = 0

Логические операции

• Над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания.
• При помощи логических связок «не», «и», «или», «если, то», «тогда и только тогда» из простых высказываний получают сложные (или составные)

Таблицы истинности

• Логические операции удобно описывать через таблицы истинности.
• Таблица истинности – это таблица, в которой отражены результаты вычислений сложных операций при различных значениях исходных простых высказываний (операндов)

1. Отрицание (инверсия)

Обозначение

Обозначение

Читается

Читается

¬А, НЕ А,

не А

не А

Значение

Значение

истинно, когда А ложно и наоборот

истинно, когда А ложно и наоборот

А

А

0

0

1

1

1

1

0

0

Операция является унарной – допускается применять к одной и более переменной

Примеры инверсии

А : Анна выучила принципы фон Неймана

¬А : Анна не выучила принципы фон Неймана

В : сегодня наша группа не будет делать генеральную уборку в кабинете

¬В : сегодня наша группа сделает генеральную уборку в кабинете

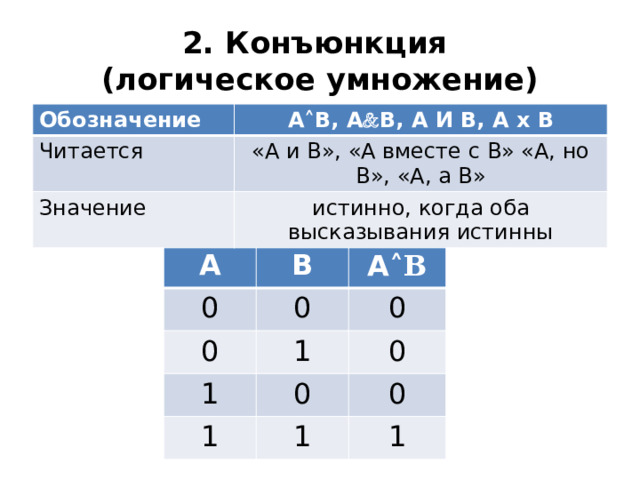
2. Конъюнкция (логическое умножение)

Обозначение

Читается

А ˄ В, А  В, А И В, А х В

«А и В», «А вместе с В» «A, но В», «А, а В»

Значение

истинно, когда оба высказывания истинны

А

0

В

0

0

А ˄В

1

0

1

1

0

0

0

1

1

Примеры конъюнкции

А : «сегодня солнечный день»

В : «мы идем гулять»

А ˄ В : «сегодня солнечный день и мы пойдем гулять»

С : «Виктор победил в соревнованиях»

D : «Богдан занял 2-е место»

C  D : «Виктор победил в соревнованиях, а Богдан занял 2-е место»

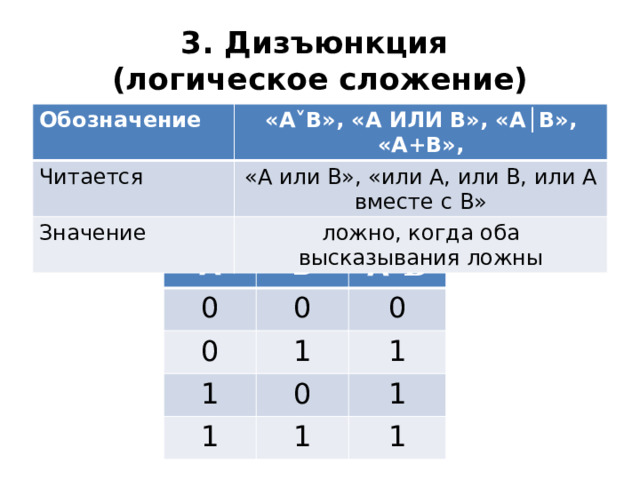
3. Дизъюнкция (логическое сложение)

Обозначение

Читается

« А ˅ В», «А ИЛИ В», «А │ В», «А + В»,

«А или В», «или А, или В, или А вместе с В»

Значение

ложно, когда оба высказывания ложны

А

0

В

0

0

А ˅В

1

0

1

1

1

0

1

1

1

Примеры дизъюнкции

А : «летом мы едем на море»

В : «летом мы едем в горы»

А  В : «летом мы поедем на море или в горы»

С : «Сергей получил 5 за экзамен»

D : «Сергей получил 4 за экзамен»

C  D : «Сергей успешно сдал экзамен»

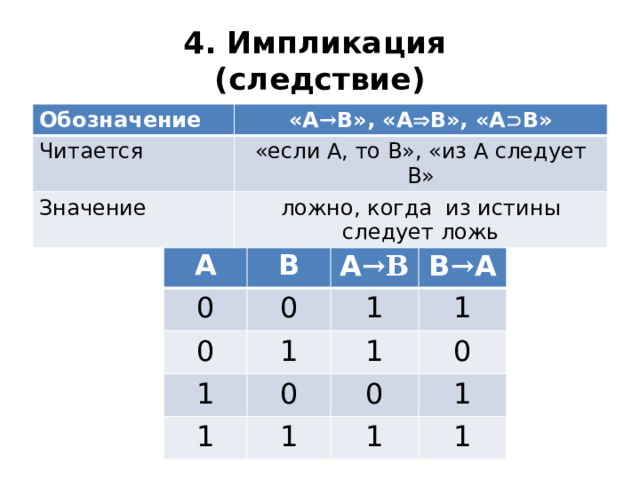
4. Импликация (следствие)

Обозначение

Читается

« А → В», «А  В», «А  В»

«если А, то В», «из А следует В»

Значение

ложно, когда из истины следует ложь

А

В

0

0

А →В

0

1

В → А

1

1

1

0

1

1

1

0

0

1

1

1

Примеры импликации

А : «на улице идет дождь»

В : «я возьму зонт»

А  В : «если на улице идет дождь, то я возьму зонт»

С : «Данил не выучит вопросы»

D : «Данил получит 2 за экзамен»

C  D : «Если Данил не выучит вопросы, то он получит 2 за экзамен»

Е : «предохранитель расплавится»

К : «электролампа гаснет»

Е  К : «если предохранитель расплавится, то электролампа погаснет»

5. Эквивалентность (логическое равенство)

Обозначение

Читается

« А ↔ В», «А ~ В», «А ≡ В», «А  В»

«А тогда и только тогда, когда В» А ттт В

Значение

«Если, и только если В, то В»

истинно, когда высказывания равны

А

0

В

0

0

А ↔В

1

1

1

1

0

0

0

1

1

Примеры эквивалентности

А : «2х5=10»

В : «40/4=10»

А ≡ В : «2х5 равно 40/4»

С : «число делится на 1 и на само себя»

D : «число простое»

C  D : «если число делится на 1 и на само себя, то оно является простым»

D  C «если число простое, то оно делится на 1 и на само себя»

C  D : «число является простым тогда и только тогда, когда оно делится на 1 и на само себя»

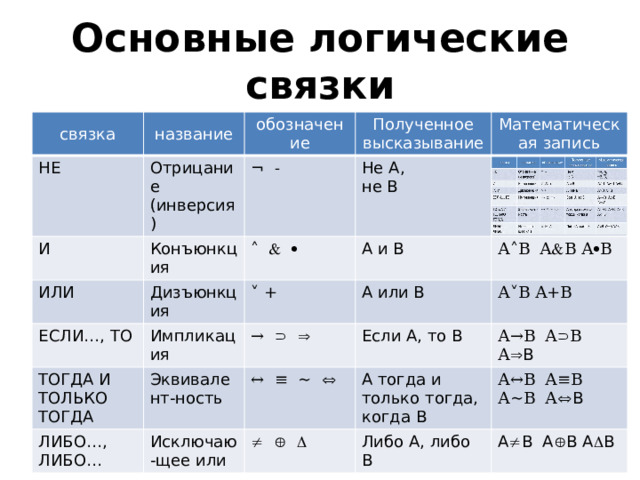
Основные логические связки

связка

связка

название

название

НЕ

НЕ

обозначение

Отрицание (инверсия)

И

Отрицание (инверсия)

И

обозначение

Полученное высказывание

Конъюнкция

Полученное высказывание

Конъюнкция

¬ -

ИЛИ

ИЛИ

¬ -

ЕСЛИ…, ТО

˄  

Математическая запись

Не А,

Не А,

Математическая запись

˄  

Дизъюнкция

ЕСЛИ…, ТО

Дизъюнкция

не В

А и В

Импликация

не В

А и В

Импликация

¬А, ,

ТОГДА И ТОЛЬКО ТОГДА

˅ +

˅ +

ТОГДА И ТОЛЬКО ТОГДА

Эквивалент-ность

А или В

А˄В А  В А  В

Эквивалент-ность

¬В, ,

→  

→  

А˄В А  В А  В

А или В

ЛИБО…, ЛИБО…

ЛИБО…, ЛИБО…

Если А, то В

Исключаю-щее или

Исключаю-щее или

Если А, то В

А˅В А+В

↔ ≡ ~ 

А˅В А+В

↔ ≡ ~ 

  

  

А тогда и только тогда, когда В

А→В А  В А  В

А→В А  В А  В

А тогда и только тогда, когда В

Либо А, либо В

Либо А, либо В

А↔В А≡В А~В А  В

А↔В А≡В А~В А  В

А  В А  В А  В

А  В А  В А  В

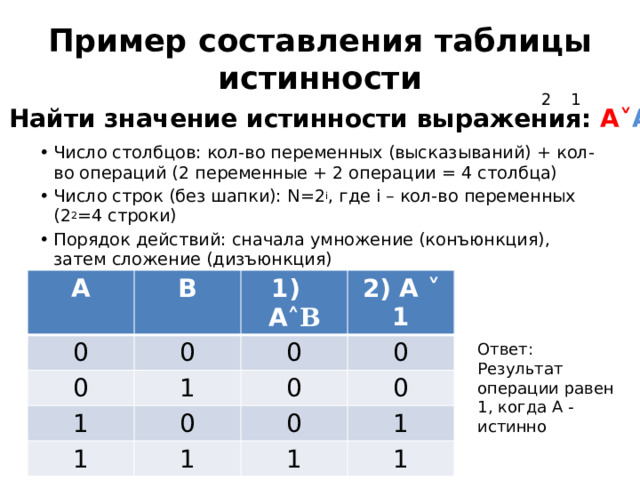
Пример составления таблицы истинности

1

2

1. Найти значение истинности выражения: А ˅ А ˄ В

• Число столбцов: кол-во переменных (высказываний) + кол-во операций (2 переменные + 2 операции = 4 столбца)
• Число строк (без шапки): N=2 i , где i – кол-во переменных (2 2 =4 строки)
• Порядок действий: сначала умножение (конъюнкция), затем сложение (дизъюнкция)

А

В

0

0

1) А ˄В

0

2) А ˅ 1

1

0

1

1

0

0

0

0

1

0

1

1

1

Ответ:

Результат операции равен 1, когда А - истинно

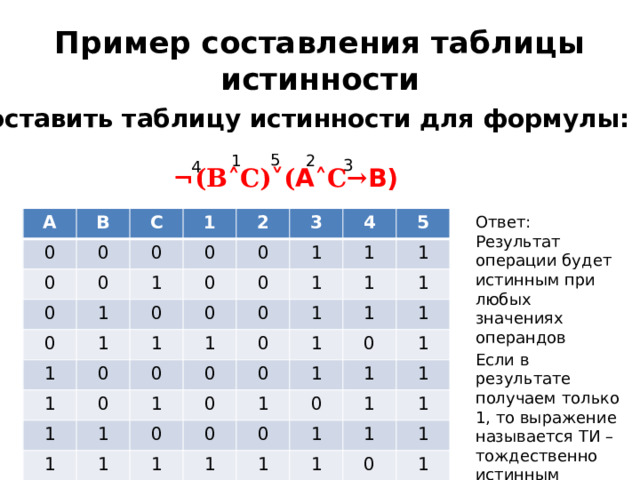
Пример составления таблицы истинности

• Составить таблицу истинности для формулы:

¬(В˄С)˅( А ˄С→ В)

5

2

1

3

4

Ответ:

Результат операции будет истинным при любых значениях операндов

А

0

В

0

С

0

0

1

0

0

0

2

1

1

0

3

0

0

0

1

1

4

0

0

1

1

0

1

0

5

1

1

1

1

0

0

1

0

0

1

1

1

1

1

1

0

1

0

1

0

1

1

0

0

1

1

1

0

1

1

0

1

1

1

1

1

1

1

1

0

1

1

Если в результате получаем только 1, то выражение называется ТИ – тождественно истинным

Задание

• Выделите в составных высказываниях простые.
• Обозначьте каждое из них буквой, запишите с помощью логических операций каждое составное высказывание

• Число 376 четное и трехзначное
• Неверно, что Солнце движется вокруг Земли
• Если сумма цифр числа делится на 3, то и всё число делится на 3
• Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3

Задание

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?

X

Y

1

1

Z

1

1

F

1

1

1

0

0

1

1

1

• X  Y  Z
•  X  Y   Z
• X   Y  Z

= 11). " width="640"

• Напишите наименьшее целое число Х, для которого истинно высказывание:

НЕ (X

• Напишите наибольшее целое число Х, для которого истинно высказывание:

НЕ (X чётное) И НЕ (X = 11).

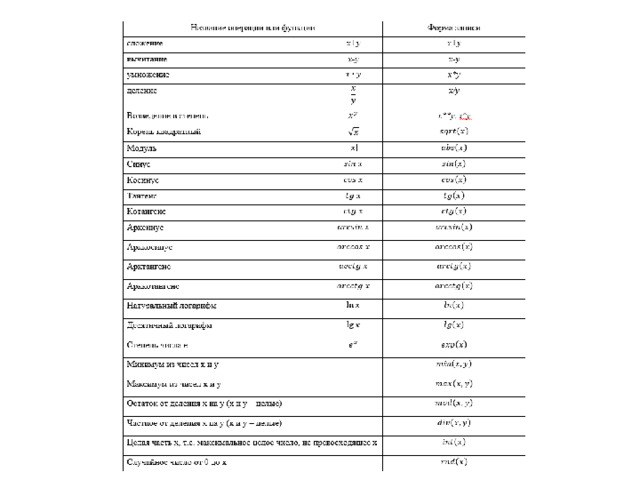
Правила записи арифметических выражений в алгоритмическом языке

• В алгоритмическом языке можно использовать не только числа. но и числовые и алгебраические выражения (формулы). В информатике эти выражения называются арифметическими.
• Правила алгоритмического языка позволяют при записи алгоритма повсюду, где можно написать число, написать и произвольное арифметическое выражение.
• Рассмотрим пример:

•  

a/2 означает ,

означает и т.д.

Правила записи арифметических выражений в алгоритмическом языке

Арифметические выражения в алгоритмическом языке должны быть записаны в так называемой линейной записи согласно следующим правилам:

• выражение должно быть записано в виде линейной цепочки символов (вместо х 1 и v 0 надо писать х1, v0);
• для обозначения операции умножения используется звездочка (*), для операции деления – косая черта (/), для операции возведения в степень – две звездочки (**) или знак возведения в степень (^);
• нельзя опускать знаки операций, например, писать 4a. Для записи произведения 4 и a надо писать 4*a;
• аргументы функций (Sin, Cos и др.), как и аргументы вспомогательных алгоритмов, записываются в круглых скобках (например, tg(x), Cos(4*a) и т.д.).
• Линейная запись позволяет вводить выражения в память компьютера, последовательно нажимая на соответствующие клавиши на клавиатуре.

Домашнее задание

Система Moodle, файл Домашние, работа 6